Teil 1 Lineare Algebra und analytische Geometrie: ohne Hilfsmittel

In einem kartesischen Koordinatensystem des $ℝ^{3}$ sind die Ebene E: $x_{1} + 2 x_{2} - x_{3} = 4$ und die Geradenschar $G_{k} : \vec{x} = (\begin{array}{c} - 3 \\ 4 \\ 1 \end{array}) + r \cdot (\begin{array}{c} - 2 \\ - k - 2 \\ k \end{array})$ mit $r, k \in ℝ$ gegeben.

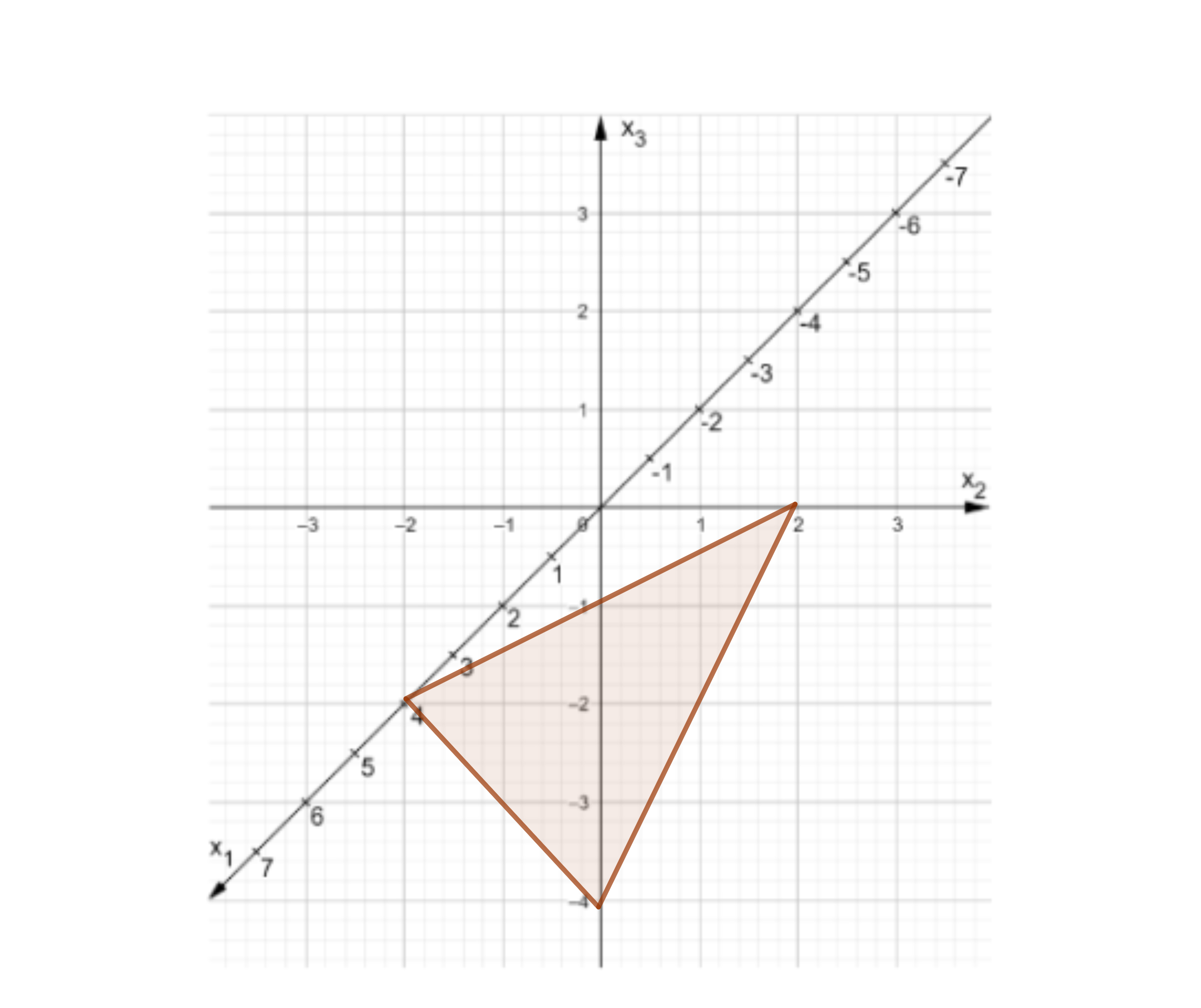
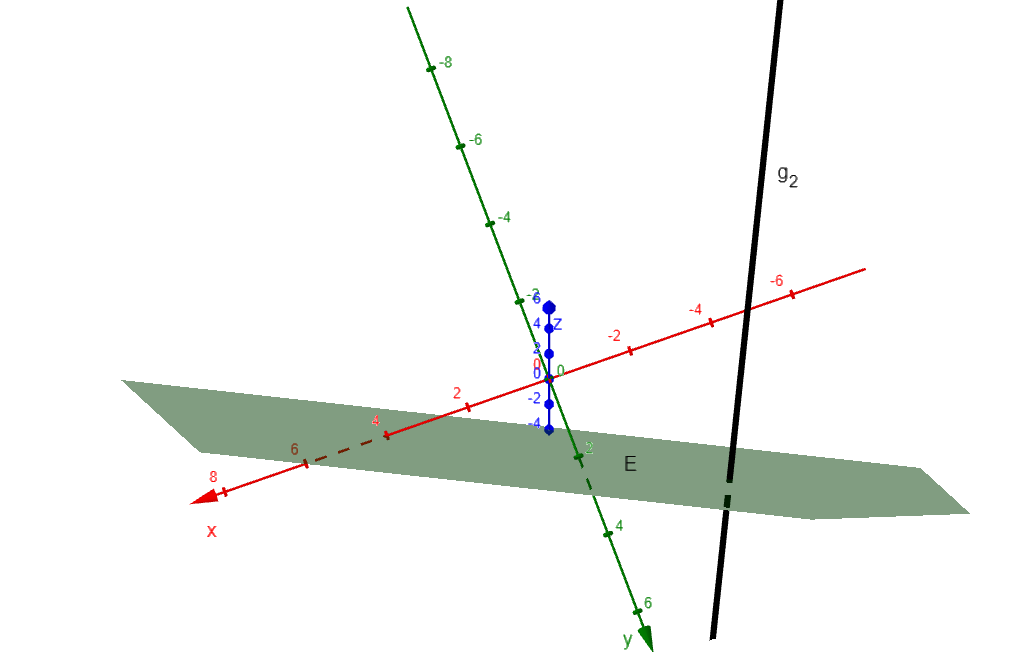
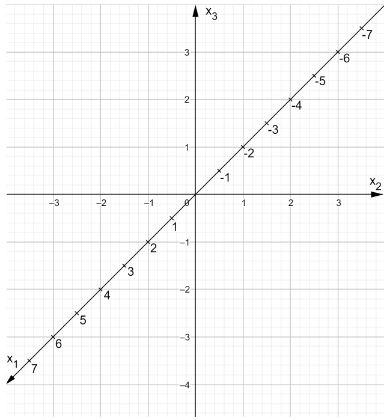
Bestimmen Sie die Schnittpunkte der Ebene $E$ mit den Koordinatenachsen und
veranschaulichen Sie die Lage der Ebene $E$ in dem nachfolgend abgebildeten
Koordinatensystem. (4 BE)
Überprüfen Sie, ob ein Wert für $k$ existiert, sodass die Gerade $g_{k}$ die Ebene $E$ senkrecht schneidet. (2 BE)
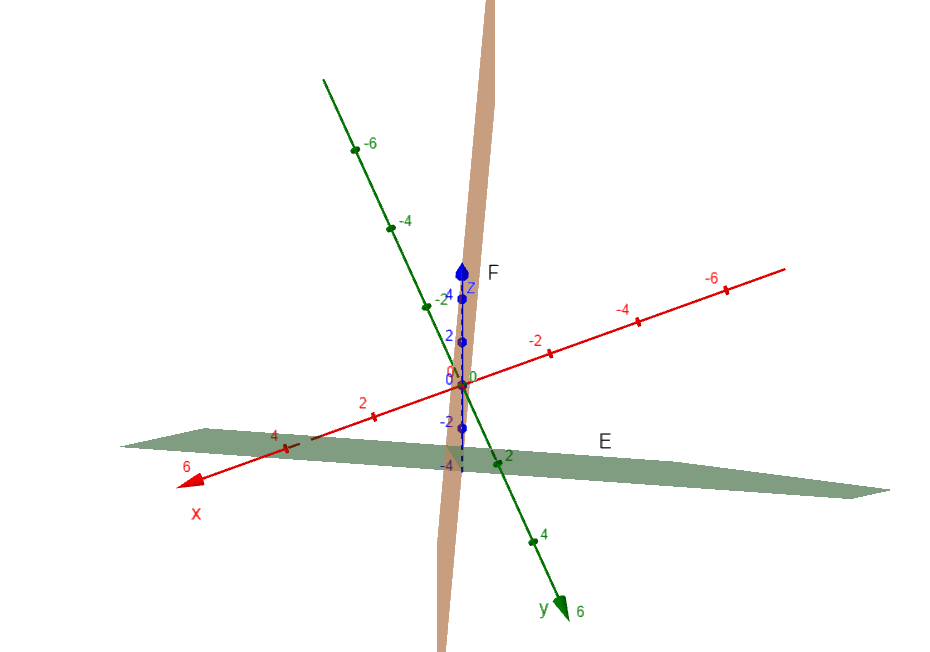
Die Ebene $F$ beinhaltet die $x_{3}$ -Achse und steht senkrecht auf der Ebene $E$ . Geben Sie eine Gleichung der Ebene $F$ in Parameterform an. (2 BE)

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?