Teil 1 Lineare Algebra und analytische Geometrie: ohne Hilfsmittel

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
In einem kartesischen Koordinatensystem des $ℝ^{3}$ sind die Ebene E: $x_{1} + 2 x_{2} - x_{3} = 4$ und die Geradenschar $G_{k} : \vec{x} = (\begin{array}{c} - 3 \\ 4 \\ 1 \end{array}) + r \cdot (\begin{array}{c} - 2 \\ - k - 2 \\ k \end{array})$ mit $r, k \in ℝ$ gegeben.
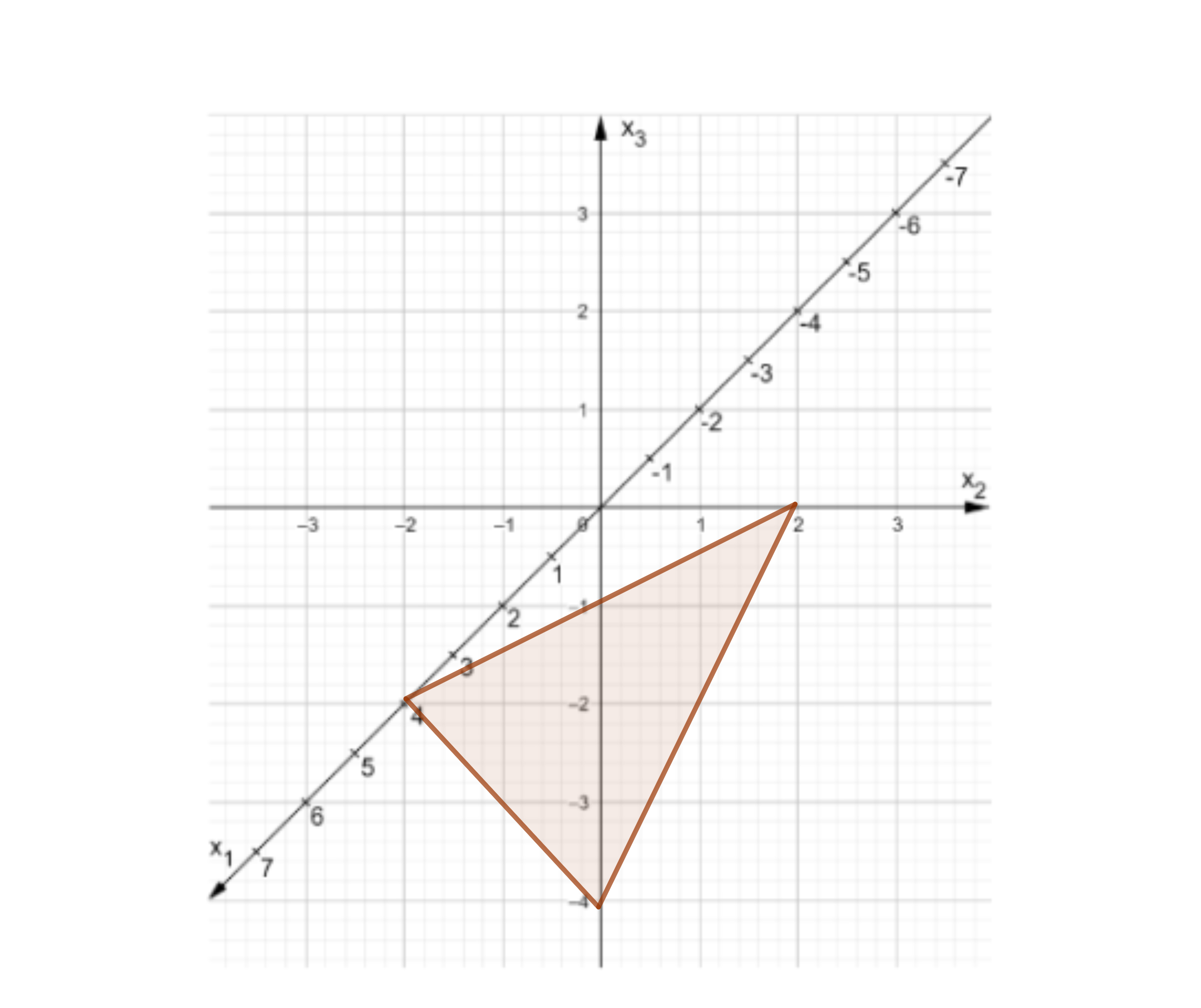
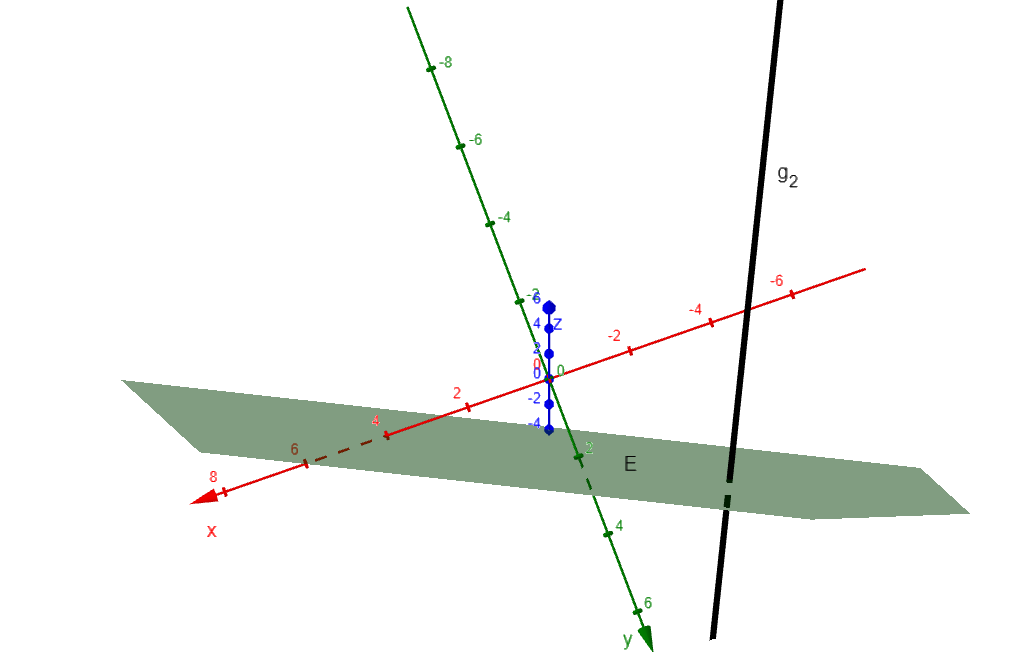
1. Bestimmen Sie die Schnittpunkte der Ebene $E$ mit den Koordinatenachsen und
  veranschaulichen Sie die Lage der Ebene $E$ in dem nachfolgend abgebildeten
  Koordinatensystem. (4 BE)
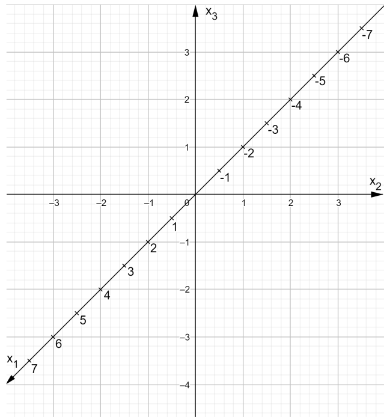
2. Überprüfen Sie, ob ein Wert für $k$ existiert, sodass die Gerade $g_{k}$ die Ebene $E$ senkrecht schneidet. (2 BE)
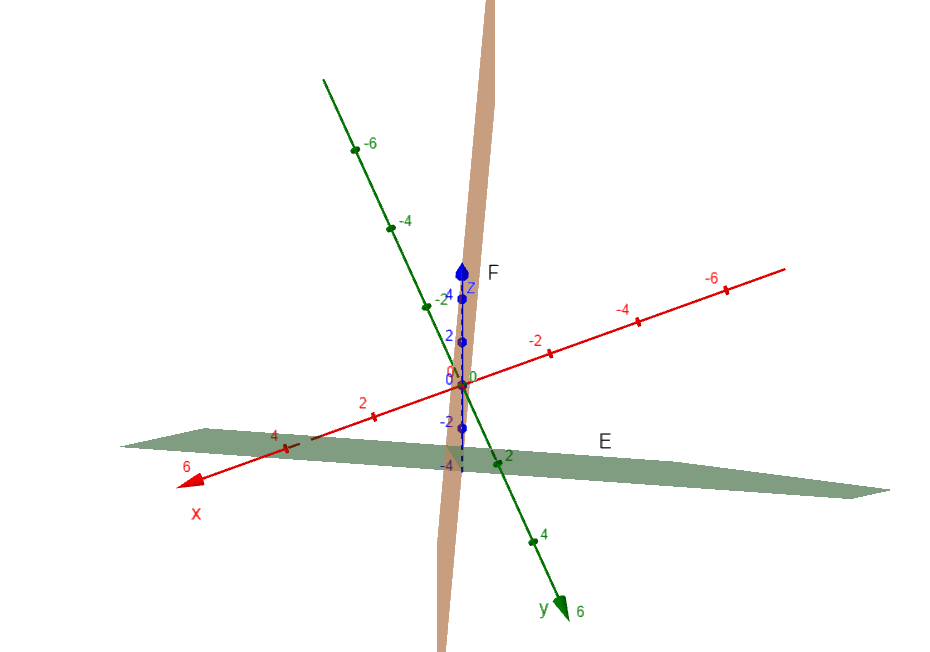
3. Die Ebene $F$ beinhaltet die $x_{3}$ -Achse und steht senkrecht auf der Ebene $E$ . Geben Sie eine Gleichung der Ebene $F$ in Parameterform an. (2 BE)
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Für die linear unabhängigen Vektoren $\vec{a}$ , $\vec{b}$ und $\vec{c}$ im $ℝ^{3}$ gelten zugleich die folgenden drei Bedingungen (1), (2) und (3):
(1) $\vec{a} \circ \vec{b} = 0$
(2) $| \vec{a} | = | \vec{b} | = 5$
(3) $\vec{c} = \frac{1}{5} (\vec{a} \times \vec{b})$
Die drei Vektoren $\vec{a}$ , $\vec{b}$ und $\vec{c}$ spannen einen Spat auf. Dabei spannen die Vektoren $\vec{a}$ und $\vec{b}$ die Grundfläche des Spats auf. Beschreiben Sie die Form des Spats und legen Sie
nachvollziehbar dar, wie Sie zu Ihren Aussagen kommen. (4 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?