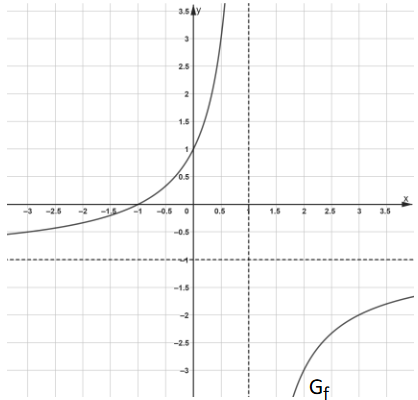
Lesen Sie jeweils die Art und die Gleichung der Asymptoten von $G_f$ ab und geben Sie diese an. (2 BE)

Gegeben ist die Funktion g durch die Gleichung $g(x)=-x$ mit $D_g=ℝ$. Der Graph der Funktion g heißt $G_g$. Zeichnen Sie $G_g$ in die obige Abbildung ein und berechnen Sie die exakten x-Koordinaten der Schnittpunkte der Graphen $G_f$ und $G_g$.

$[$ Teilergebnis: $x=1+\sqrt{2}$$]$

(5 BE)

Gegeben sind die bestimmten Integrale

$${\displaystyle {\int }_1^{1+\sqrt{2}}(-1-g(x))\mathrm{d}x}$$ und $${\displaystyle {\int }_{1+\sqrt{2}}^3(-1-f(x))\mathrm{d}x}$$

Die Integralwerte können jeweils geometrisch als Flächenmaßzahl eines Flächenstückes im Koordinatensystem der Aufgabe a) interpretiert werden. Kennzeichnen Sie die beiden Flächenstücke in der Zeichnung der Aufgabe a). (3 BE)

Die reelle Funktion $h:x\to \ln (f(x))$ besitzt den maximalen Definitionsbereich

$D_h=]-1;1]$. Der Graph der Funktion $h$ heißt $G_h$. Der Graph $G_h$ ist punktsymmetrisch zum Ursprung des Koordinatensystems.

(Nachweis nicht erforderlich!).

1) Ermitteln Sie mithilfe von $G_f$ das Verhalten der Funktionswerte von $h$ bei Annäherung an die Ränder von $D_h$. Geben Sie die Gleichungen aller Asymptoten von $G_h$ an. (4 BE)

2) Bestätigen Sie rechnerisch, dass $G_h$ keine relativen Extrempunkte besitzt.

$[$mögliches Teilergebnis: $${\displaystyle h^{\prime }(x)=\frac{-2}{x^2-1}}$$$]$ (6 BE)

3) Zeichnen Sie $G_h$ mit seinen Asymptoten in das Koordinatensystem von Aufgabe a) ein. (4 BE)