Teil 2 Analysis II: mit Hilfsmitteln

Gegeben ist die Funktion $f$ durch die Gleichung $f (x) = \frac{x^{3} - 3 x + 2}{x^{2}}$ mit ihrer maximalen

Definitionsmenge $D_{f} = ℝ$ \{ $0$ } . Der Graph von $f$ wird mit $G_{f}$ bezeichnet.

Zeigen Sie, dass $f (x)$ zu jedem der beiden folgenden Terme äquivalent ist:
$\frac{(x - 1)^{2} (x + 2)}{2}$
x $- \frac{3}{x} + \frac{2}{x^{2}}$
Hinweis: Für alle drei Darstellungsformen der Funktion $f$ gilt: $D_{f} = ℝ$ \{ $0$ }
(Nachweis nicht erforderlich) (3 BE)
Geben Sie die Nullstellen von $f$ mit ihrer jeweiligen Vielfachheit an. (2 BE)
Geben Sie zu jeder Asymptote von $G_{f}$ deren Art und Gleichung an. (2 BE)
Ermitteln Sie die maximalen Monotonieintervalle von $G_{f}$ und geben Sie die Art seines einzigen lokalen Extrempunktes an.
$[$ mögliches Teilergebnis: $f^{'} (x) = \frac{x^{3} + 3 x - 4}{x^{3}}$ $]$ (9 BE)
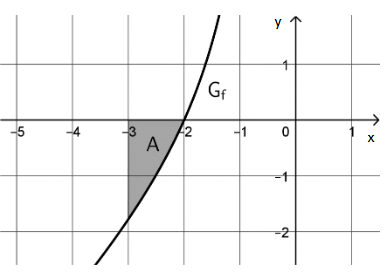
Die Abbildung zeigt ein endliches Flächenstück $A$ , das unter anderem von $G_{f}$ begrenzt wird. Berechnen
Sie die Maßzahl seines Flächeninhalts.
Hinweis: Die ganzzahligen
Grenzen des Flächenstücks
dürfen der Abbildung
entnommen werden.
(4 BE)