Teil 2 Analysis II: mit Hilfsmitteln
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Gegeben ist die Funktion durch die Gleichung mit ihrer maximalen Definitionsmenge \{} . Der Graph von wird mit bezeichnet.
Zeigen Sie, dass zu jedem der beiden folgenden Terme äquivalent ist:
Hinweis: Für alle drei Darstellungsformen der Funktion gilt: \{} (Nachweis nicht erforderlich) (3 BE)
Geben Sie die Nullstellen von mit ihrer jeweiligen Vielfachheit an. (2 BE)
Geben Sie zu jeder Asymptote von deren Art und Gleichung an. (2 BE)
Ermitteln Sie die maximalen Monotonieintervalle von und geben Sie die Art seines einzigen lokalen Extrempunktes an.
mögliches Teilergebnis: (9 BE)
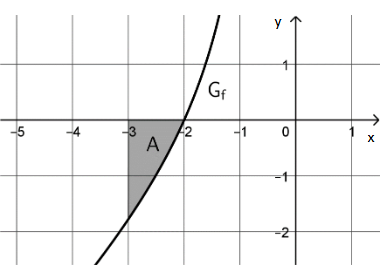
Die Abbildung zeigt ein endliches Flächenstück , das unter anderem von begrenzt wird. Berechnen
Sie die Maßzahl seines Flächeninhalts.
Hinweis: Die ganzzahligen
Grenzen des Flächenstücks
dürfen der Abbildung
entnommen werden.
(4 BE)
- 2
Gegeben ist die Funktion mit ihrer maximalen Definitionsmenge . Der Graph von wird mit bezeichnet.
Untersuchen Sie das Verhalten der Funktionswerte von bei Annäherung an die Ränder von . (3 BE)
Ermitteln Sie die Art und die Koordinaten des relativen Extrempunktes und die exakten Koordinaten des Wendepunktes von .
mögliches Teilergebnis: (8 BE)
Zeigen Sie mithilfe partieller Integration, dass die Funktion mit und eine Stammfunktion von ist. (5 BE)
Nun wird zusätzlich die Funktion mit der Definitionsmenge und der Gleichung betrachtet. Es gilt also für alle . Der Graph von wird mit bezeichnet. Lässt man um die x-Achse rotieren, entsteht ein Rotationskörper (siehe Abbildung), welcher als Modell für den Kelch eines Saftglases dient. Die Koordinaten der Punkte sind Längenangaben in der Einheit Zentimeter. Auf die Mitführung der Einheiten kann bei den folgenden Rechnungen verzichtet werden. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen.
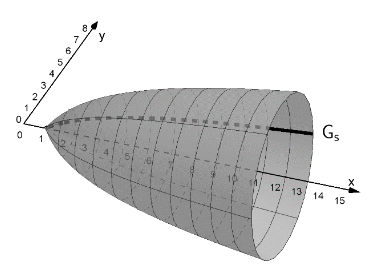
1) Die Volumenmaßzahl des obigen Rotationskörpers kann mit dem Integral berechnet werden. Zeigen Sie rechnerisch, dass das Saftglas ein maximales Flüssigkeitsvolumen von ca. aufnehmen kann. (4 BE)
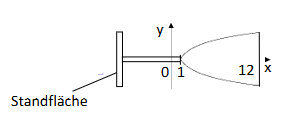
2) Die Standfläche des Saftglases soll kreisförmig sein und den gleichen Durchmesser wie die Querschnittsfläche des Rotationskörpers für haben. Ermitteln Sie die Maßzahl des Flächeninhalts dieser Standfläche. (3 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
