Untersuchen Sie das Verhalten der Funktionswerte von $h$ bei Annäherung an die Ränder von $D_h$. (3 BE)

Ermitteln Sie die Art und die Koordinaten des relativen Extrempunktes und die exakten Koordinaten des Wendepunktes von $G_h$.

$[$ mögliches Teilergebnis: $${\displaystyle h^{\prime }(x)=\frac{\mathrm{4,5}\ln (x)}{x}}$$ $]$ (8 BE)

Zeigen Sie mithilfe partieller Integration, dass die Funktion $H$ mit

$H(x)=\mathrm{2,25}\cdot x\cdot {\left[\ln \left(x\right)\right]}^2-\mathrm{4,5}\cdot x\cdot \ln \left(x\right)+\mathrm{4,5}\cdot x$ und $D_H={ℝ}^{+}$ eine Stammfunktion von $h$ ist. (5 BE)

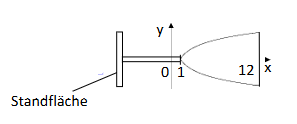
Nun wird zusätzlich die Funktion $s$ mit der Definitionsmenge $D_s=[1;12]$ und der

Gleichung $s(x)=\mathrm{1,5}\cdot \ln (x)$ betrachtet. Es gilt also $[s(x){]}^2=h(x)$für alle $x\in D_s$. Der Graph von $s$ wird mit $G_s$ bezeichnet. Lässt man $G_s$ um die x-Achse rotieren, entsteht ein Rotationskörper (siehe Abbildung), welcher als Modell für den Kelch eines Saftglases dient. Die Koordinaten der Punkte sind Längenangaben in der Einheit Zentimeter. Auf die Mitführung der Einheiten kann bei den folgenden Rechnungen verzichtet werden. Runden Sie Ihre Ergebnisse auf zwei

Nachkommastellen.

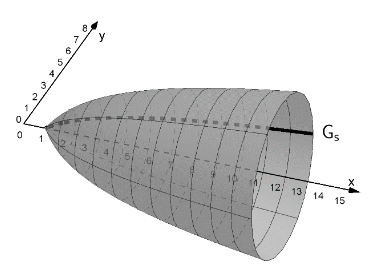
1) Die Volumenmaßzahl $V$ des obigen Rotationskörpers kann mit dem Integral

$$V(s)=\pi \cdot {\displaystyle {\int }_1^{12}{\left[s\left(x\right)\right]}^2\mathrm{d}x}$$ berechnet werden. Zeigen Sie rechnerisch, dass das Saftglas ein maximales Flüssigkeitsvolumen von ca. $257\text{ ml}$ aufnehmen kann. (4 BE)

2) Die Standfläche des Saftglases soll kreisförmig sein und den gleichen Durchmesser wie die Querschnittsfläche des Rotationskörpers für $x=12$ haben. Ermitteln Sie die Maßzahl des Flächeninhalts dieser Standfläche. (3 BE)