Aufgabe 6
Die Aufgabe 6 ist eine Fortsetzung der Aufgabe 1.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für die Funktion mit .
Dabei entspricht eine Längeneinheit im Koordinatensystem in der Realität.
Siehe Abbildung 2:
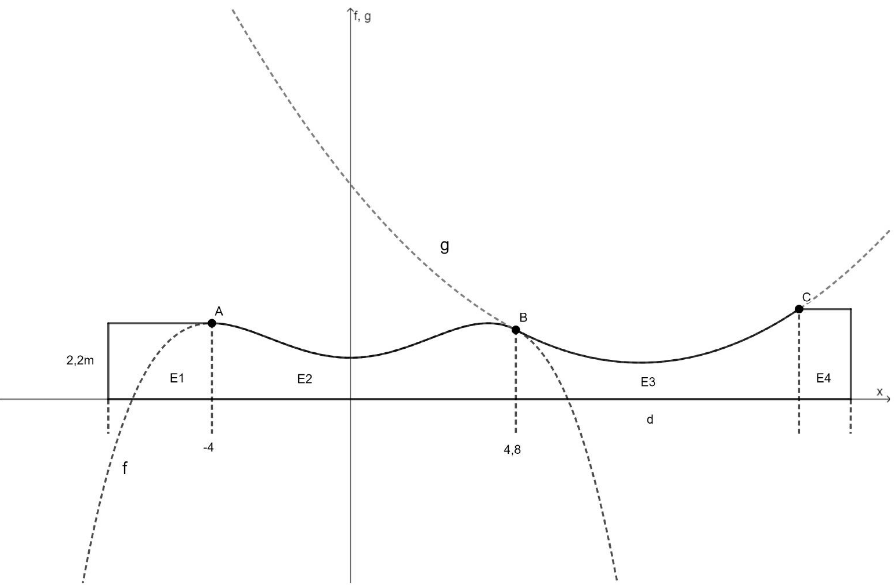
Abbildung 2
In einem anderen Skatepark soll der Abschnitt E2 vergleichbar gebaut werden, allerdings soll der Streckenverlauf in diesem Abschnitt steiler sein. Zur Modellierung dient hier eine Funktion mit
.
Zeigen Sie, dass gilt, und begründen Sie, dass für jedes die Lage und Art der Extremstellen von mit der Lage und Art der Extremstellen von übereinstimmen. (1 P + 2 P)
Ermitteln Sie den Wert von , bei dem diese Bahn im Abschnitt E2 an der Stelle die Steigung hat. (2 P)
