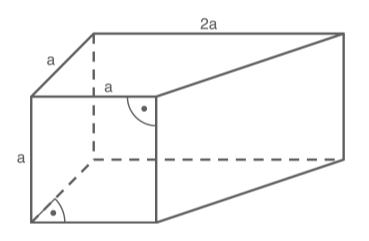
Teilt man das Trapezprisma in einen Würfel und ein Prisma auf, so kann man sein Volumen in Abhängigkeit von $a$ ausdrücken.

Das Volumen des Würfels

Die Seiten des Würfels haben eine Länge von $a$. Um sein Volumen zu berechnen, multipliziert man Länge mit Höhe und Breite:

$V_{W\ddot{u}rfel}=l_{W\ddot{u}rfel}\cdot h_{W\ddot{u}rfel}\cdot b_{W\ddot{u}rfel}=a\cdot a\cdot a=a^3$

Das Volumen des Dreiecksprismas

Um das Volumen des Dreiecksprismas zu berechnen, multipliziert man seine Grundfläche mit seiner Höhe.

Die Grundfläche ist ein rechtwinkliges Dreieck, dessen Katheten die Länge $a$ haben. Damit kann man die Fläche dieses Dreiecks ausrechnen:

$G=\frac{1}{2}\cdot a\cdot h_a=\frac{1}{2}\cdot a\cdot a=\frac{1}{2}\cdot a^2$

Jetzt muss man die Grundfläche nur noch mit der Höhe multiplizieren, um das Volumen zu berechnen:

$V_{\text{Dreiecksprisma}}=G\cdot h=\frac{1}{2}\cdot a^2\cdot a=\frac{1}{2}\cdot a^3$

Das Volumen des Dreiecksprismas ist genau halb so groß wie das des Würfels.

Das Volumen des Trapezprismas kann man jetzt bestimmen, indem man das Volumen des Würfels und das Volumen des Dreiecksprismas addiert:

$V_{Trapezprisma}=V_{W\ddot{u}rfel}+V_{Prisma}=a^3+\mathrm{0,5}\cdot a^3=\mathrm{1,5}\cdot a^3$

Jetzt kann man die Formeln in den Antwortmöglichkeiten ebenfalls in Abhängigkeit von $a$ formulieren und mit diesem Ergebnis vergleichen.

Antwortmöglichkeit 1

${\text{Volumen}}_1=2\cdot {\text{Volumen}}_{\text{Würfel}}+{\text{Volumen}}_{\text{Dreiecksprisma}}=2\cdot a^3+\mathrm{0,5}\cdot a^3=\mathrm{2,5}\cdot a^3$

$\mathrm{2,5}\cdot a^3\ne \mathrm{1,5}\cdot a^3$

Antwortmöglichkeit 1 ist also falsch.

Antwortmöglichkeit 2

${\text{Volumen}}_2={\text{Volumen}}_{\text{Würfel}}+{\text{Volumen}}_{\text{Dreiecksprisma}}=a^3+\mathrm{0,5}\cdot a^3=\mathrm{1,5}\cdot a^3$

$\mathrm{1,5}\cdot a^3=\mathrm{1,5}\cdot a^3$

Antwortmöglichkeit 2 ist also richtig.

Antwortmöglichkeit 3

${\text{Volumen}}_3=2\cdot {\text{Volumen}}_{\text{Dreiecksprisma}}-{\text{Volumen}}_{\text{Würfel}}=2\cdot \mathrm{0,5}\cdot a^3-a^3=a^3-a^3=0$

$0\ne \mathrm{1,5}\cdot a^3$

Antwortmöglichkeit 3 ist also falsch.

Antwortmöglichkeit 4

${\text{Volumen}}_4=2\cdot {\text{Volumen}}_{\text{Würfel}}+{\displaystyle \frac{1}{2}}\cdot {\text{Volumen}}_{\text{Würfel}}=2\cdot a^3+{\displaystyle \frac{1}{2}}\cdot a^3=\mathrm{2,5}\cdot a^3$

$\mathrm{2,5}\cdot a^3\ne \mathrm{1,5}\cdot a^3$

Antwortmöglichkeit 4 ist also falsch.