Zwei defekte Computermonitore sind mit zwei guten zusammengepackt worden. Man prüft die Monitore der Reihe nach, bis man weiß, welche die zwei fehlerhaften sind. Mit welcher Wahrscheinlichkeit ist man nach Prüfung des zweiten Monitors, mit welcher Wahrscheinlichkeit erst nach Prüfung des dritten fertig?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Es gibt in dieser Aufgabe insgesamt vier Monitore: Zwei kaputte und zwei gute. Es wird ohne Zurücklegen ein Monitor nach dem anderen gezogen und nachgesehen, ob er kaputt ist oder nicht.
Folgende Bezeichnungen für die Ereignisse kannst du hier einführen:
K=der angesehene Monitor ist kaputt
G=der angesehene Monitor ist gut
Um die Wahrscheinlichkeiten aus der Aufgabenstellung zu berechnen, stellst du ein Baumdiagramm auf:
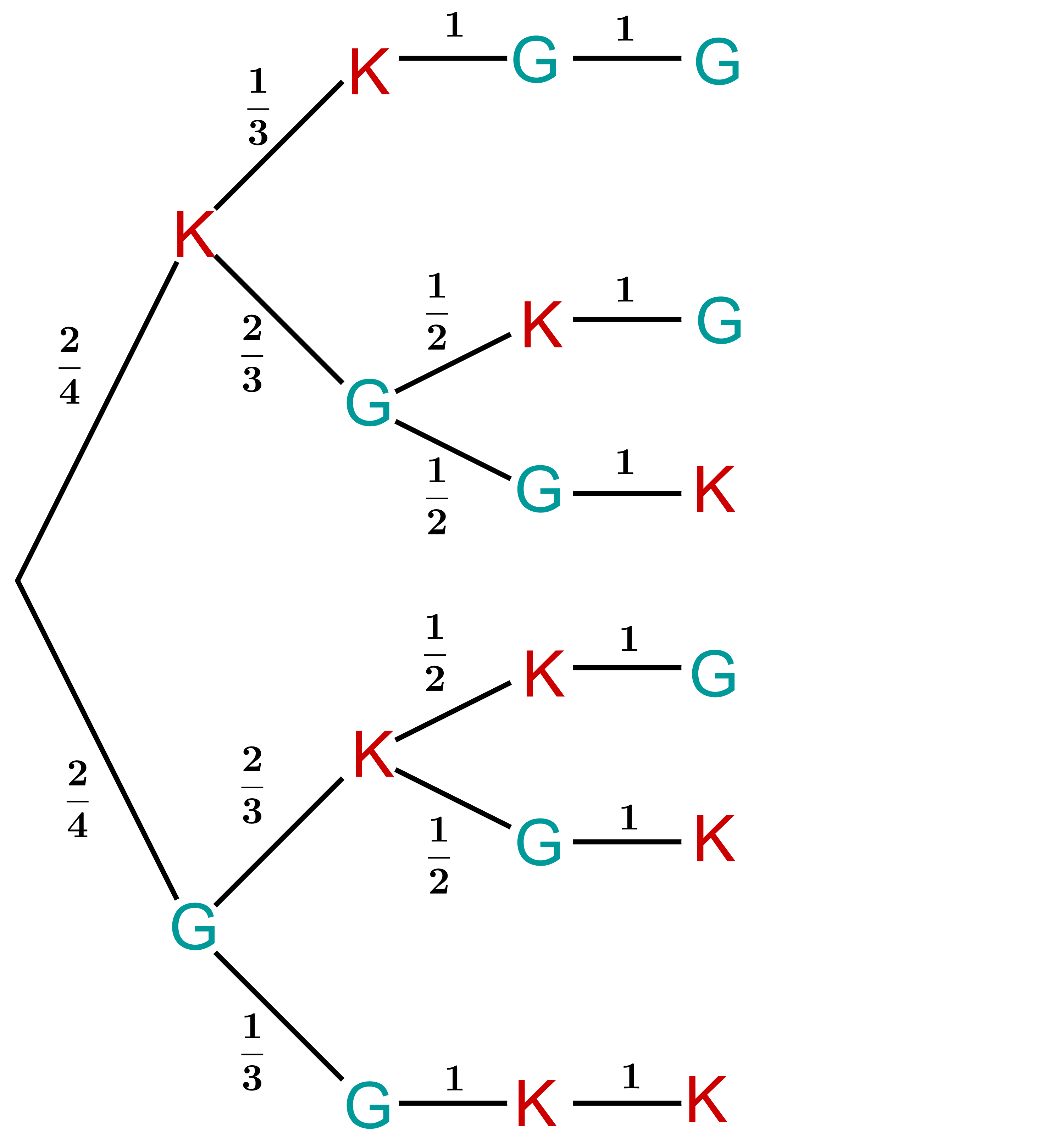
Da man ohne zurücklegen zieht, ändern sich mit jeder Überprüfung die Wahrscheinlichkeiten.
Überlege dir nun, welche Pfade zu den Ereignissen passen, die in der Aufgabenstellung genannt werden.
Fertig nach zwei Überprüfungen
Bei welchen Pfaden weiß man nach zwei überprüften Monitoren schon, welche die kaputten Monitore sind? Das sind genau die Pfade, bei denen es nach dem zweiten Schritt keine Verzweigung mehr gibt. Es gibt also zwei mögliche Pfade:
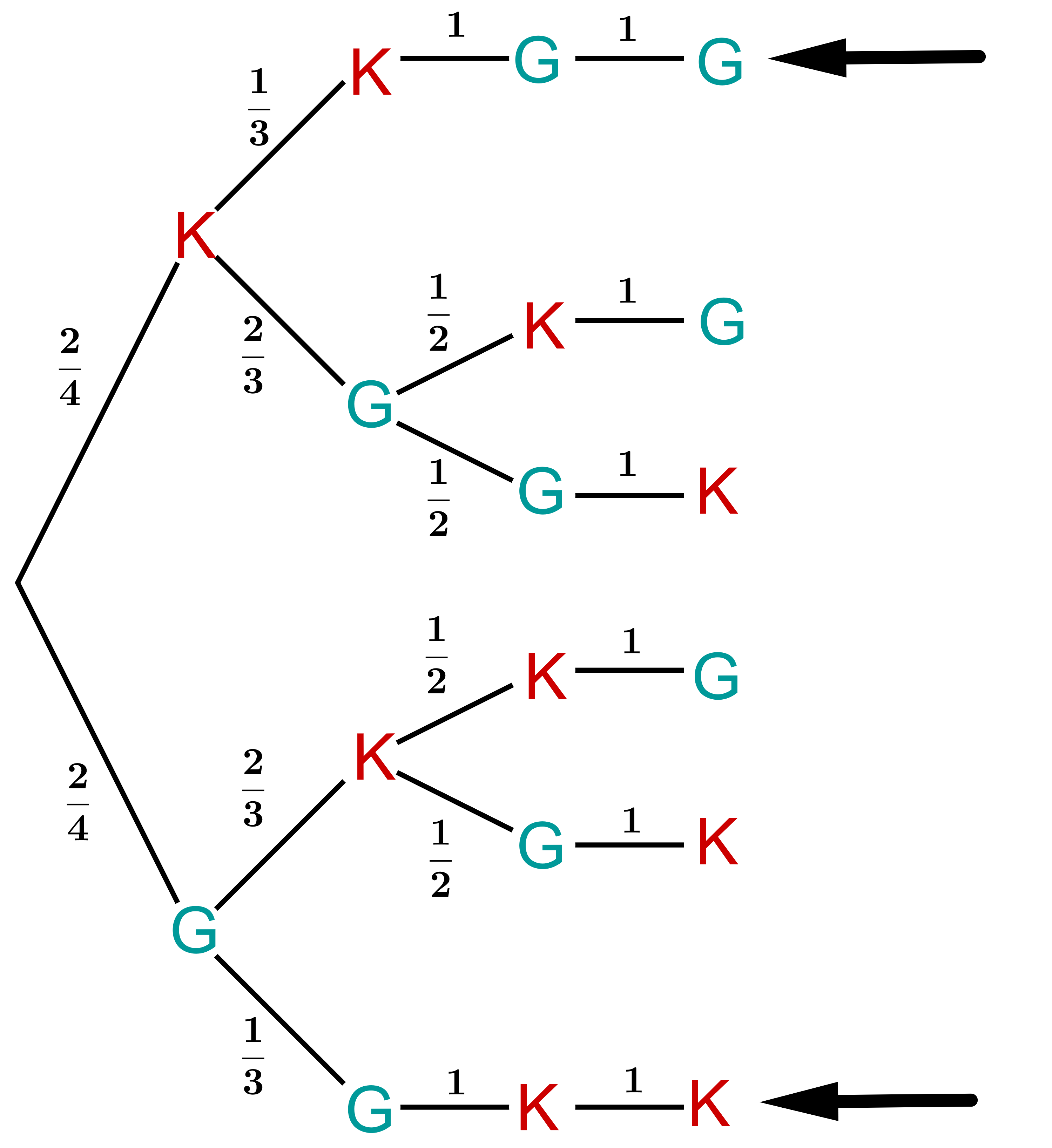
Die ersten beiden Monitore, die angesehen werden, sind kaputt. Das entspricht dem Pfad KKGG. Dieser Pfad hat die Wahrscheinlichkeit P(KKGG)=42⋅31⋅1⋅1=122=61.
Die ersten beiden Monitore sind gut. Das entspricht dem Pfad GGKK. In diesem Fall sind genau die beiden übrigen Monitore die kaputten. Der Pfad hat die Wahrscheinlichkeit P(GGKK)=42⋅31⋅1⋅1=122=61.
Weil es bei den anderen Pfaden im zweiten Schritt immernoch eine Verzweigung gibt, kommen diese Pfade nicht mehr infrage.
Die Wahrscheinlichkeit dafür, nach zwei Überprüfungen fertig zu sein, ist also:
Fertig nach drei Überprüfungen
Eine Möglichkeit, die Wahrscheinlichkeit zu ermitteln, mit der man nach drei Überprüfungen fertig ist, ist, wieder die Wahrscheinlichkeiten der entsprechenden Pfade auszurechnen und zu Addieren. Eine weitere Möglichkeit, die etwas Arbeit spart, ist, mit der Gegenwahrscheinlichkeit zu argumentieren:
Sieh dir die Pfade an, bei denen man nicht nach zwei Überprüfungen fertig ist. Das sind alle Pfade außer KKGG und GGKK.
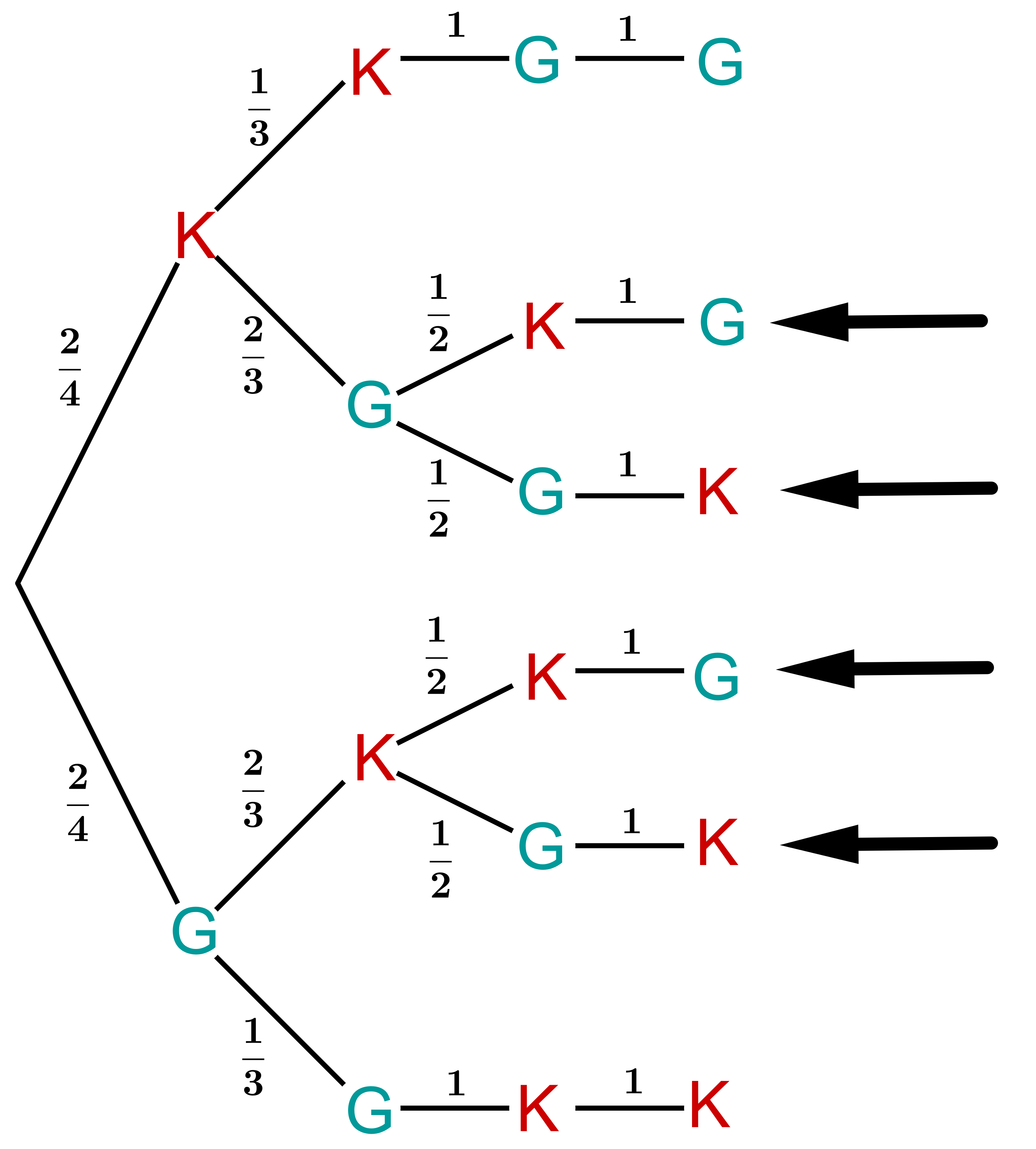
Bei all diesen Pfaden weiß man nach der dritten Überprüfung schon, welche die kaputten Monitore sind. Denn dann kann man schließen, ob der vierte kaputt ist oder nicht. Das heißt:
Das Ereignis "nach drei U¨berpru¨fungen fertig" ist genau das Gegenereignis zu "nach zwei U¨berpru¨fungen fertig". Und die Wahrscheinlichkeit, nach zwei Überprüfungen fertig zu sein, hast du oben schon berechnet. Daher gilt:
Erstelle zunächst ein Baumdiagramm (Ziehen ohne Zurücklegen). Berechne dann die gesuchten Wahrscheinlichkeiten mithilfe der Pfadregeln. Auch die Betrachtung eines Gegenereignisses kann hilfreich sein.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
