Beispiel
Du kannst z.B. aus der Tier-Relation aus Kapitel 6 durch Entfernen von Paaren (bzw. Pfeilen) eine Abbildung machen:
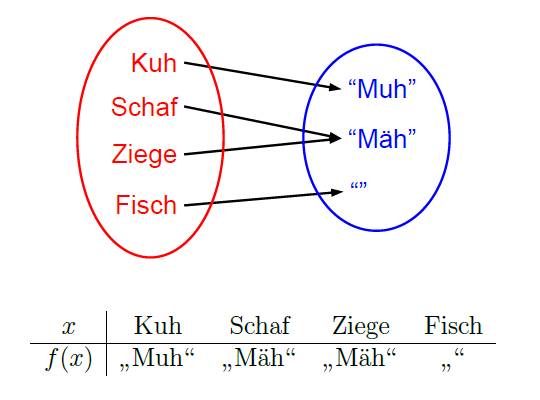
Diese Tabelle ist die Wertetabelle der Abbildung.
Definitionsbereich und Wertevorrat
Für eine Funktion heißt der Definitionsbereich und der Wertevorrat von . Beide gehören zur Funktion!
Daher sind mit und mit zwei verschiedene Abbildungen!
Bildmenge und Urbildmenge
Der Wertevorrat muss nicht ausgeschöpft werden. Die Menge der Elemente des Wertevorrats , die tatsächlich als Bildelemente auftreten, heißt die Bildmenge (auch: das Bild) von (unter ):
Zu einem ist
die Urbildmenge (auch: das Urbild) von . Vorsicht: ist ein einzelnes Element, aber ist eine Menge mit eventuell mehreren oder keinen Elementen.
Injektivität, Surjektivität und Bijektivität
Es folgen drei Begriffe, die zum Glück nicht so kompliziert sind, wie sie klingen.
Eine Abbildung heißt
injektiv, wenn gilt:
d.h. jedes aus dem Wertevorrat hat höchstens ein Urbild.
surjektiv, wenn gilt:
d.h. jedes aus dem Wertevorrat hat mindestens ein Urbild.
bijektiv, wenn gilt:
d.h. jedes aus dem Wertevorrat hat genau ein Urbild.
Bijektiv bedeutet also injektiv und surjektiv. Bei einer bijektiven Abbildung ist die Umkehrung ebenfalls eine Abbildung.
Der deutsche Begriff für injektiv lautet eineindeutig - die Abbildung ist eindeutig, und die Umkehrung ist auch eindeutig. Der deutsche Begriff für surjektiv lautet auf - die Elemente des Definitionsbereichs werden auf den Wertevorrat abgebildet und nicht nur in den Wertevorrat. Und der deutsche Begriff für bijektiv lautet umkehrbar eindeutig.
Beispiele
Die Funktion ist nicht injektiv. Denn beispielsweise werden sowohl als auch werden auf abgebildet. Die hat also die Urbildmenge .
Die Funktion ist auch nicht surjektiv, denn die negativen Zahlen treten nicht als Bildelemente auf.
Wenn du den Definitionsbereich und den Wertevorrat auf die positiven reellen Zahlen einschränkst, erhältst du eine injektive und surjektive, also bijektive Abbildung .
Abzählbarkeit
Eine Menge ist abzählbar genau dann, wenn es eine bijektive Abbildung zwischen und gibt. Dadurch ergibt sich quasi ein Nummerierung der Elemente von .
Beispiel
Die Menge der ganzen Zahlen ist abzählbar. Eine bijektive Abbildung ist gegeben durch
Die Zahlen werden also auf die geraden Zahlen abgebildet, die negativen Zahlen werden auf die ungeraden Zahlen abgebildet.
Die Menge der rationalen Zahlen ist abzählbar. Die Menge der reellen Zahlen ist dagegen nicht abzählbar. Du beweist diese beiden Tatsachen mit dem ersten bzw. mit dem zweiten cantorschen Diagonalverfahren.
Laden
Laden
Laden
