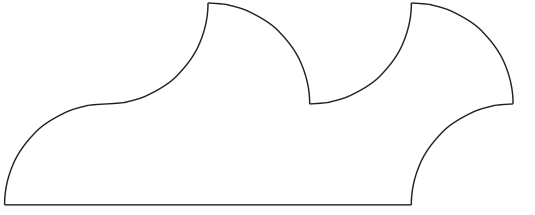
Zerlege folgende Figur durch genau eine gerade oder gekrümmte Linie in zwei kongruente (deckungsgleiche) Teilfiguren.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Zerlege folgende Figur durch genau eine gerade oder gekrümmte Linie in zwei kongruente (deckungsgleiche) Teilfiguren.
