Einführungskurs zur Ableitung

1 Einführungskurs Ableitung

Achtung! Dieser Kurs befindet sich noch in Arbeit!

Inhalt des Kurses: In diesem Kurs lernst du am Beispiel einer Halfpipe, wie du Steigungen an bestimmten Stellen annähern und letztendlich berechnen kannst.

Vorkenntnisse:

Steigungen von Geraden
Die Begriffe Sekante und Tangente
Grenzwerte mit Limes berechnen

Kursdauer: 120 min

2 Geometrie einer Halfpipe

Patrick ist ein begeisterter Skater. Im Urlaub sieht er eine Halfpipe, die ihm steiler vorkommt als die Halfpipe auf der er Zuhause immer skatet. Er fragt sich, ob es eine Möglichkeit gibt, herauszufinden, wie steil sie ist und wie man sie mit einer anderen vergleichen kann.

Hast du eine Idee?

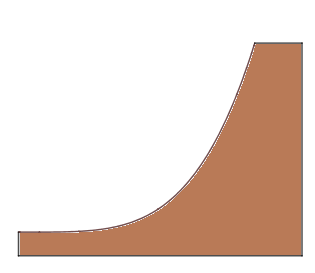
3 Mögliche Bestimmung der Steigung

Um die Steigung zu bestimmen, legt Patrick eine Stange, die er auf dem Boden gefunden hat, auf die Halfpipe. Aus der Schule weiß er, dass er für die Durchschnittliche Steigung einer Gerade den Höhenunterschied von Anfangs- und Endpunkt benötigt, sowie die Strecke von Anfangs- und Endpunkt parallel zum Boden. Also misst er mit einem Meterstab die gesuchten Abstände aus.

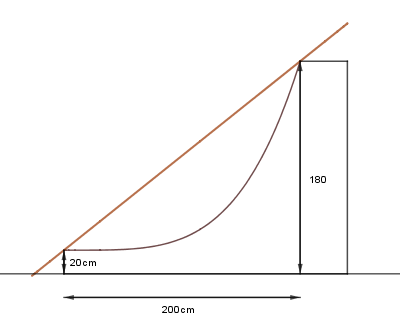
Die Steigung $m$ berechnet er, indem er Höhe durch Strecke teilt.

$m=\frac{Höhe}{Strecke}=\frac{\Delta h}{\Delta s}=\frac{180-20}{200}=\frac{160}{200}=\frac{4}{5}=0{,}8$

4 Sekantensteigung an beliebigen Stellen

Was Patrick gerade verwendet hat,um die Steigung der Halfpipe zu bestimmen, war die Steigung der Sekante, die durch die beiden Endpunkte der Halfpipe verläuft.

Beim Vergleichen von seinem Ergebnis und der Halfpipe sieht er sofort: die Steigung ist nicht an jeder Stelle gleich! Er hat die durchschnittliche Steigung bestimmt, wie kann er also die Steigung genauer bestimmen, sodass er mit seinem Ergebnis die Steigung an einer bestimmten Stelle (wie die Mitte der Halfpipe) besser annähern kann?

Eine Möglichkeit dazu, eine genauere Steigung zu bestimmen, ist, eine kleinere Stange zu verwenden und nur ein spezielles Stück der Halfpipe zu vermessen. Diese legt er an einer beliebgen Stelle auf die Halfpipe und misst erneut Höhe und Strecke (parallel zum Boden) der beiden Berührungspunkte von Stange und Halfpipe. Mit diesen Werten lässt sich eine genauere Steigung an dieser Stelle berechnen.

$m=\frac{h}{s}=\frac{80 cm}{40 cm}=2$

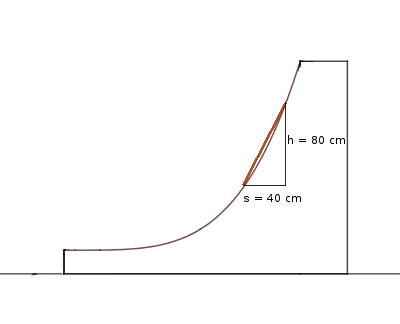
5 Differenzenquotient

Was Patrick gerade mit Stangen an verschiedenen Positionen gemessen hat, kann man bei jeder stetigen Funktion im Koordinatensystem mithilfe von Sekanten und deren Steigung ebenfalls durchführen, um eine mittlere Steigung zwischen zwei Punkten zu erhalten.

Schau dir zum Beispiel die Funktion $f (x) = x^{2} + x - 2$ an.

Du willst die mittlere Steigung zwischen dem x-Wert 1 und dem x-Wert 2 bestimmen. Dazu legst du eine Gerade $g$ an die Funktion $f$ , die durch die Punkte $A (1 ∣ f (1))$ und $B (2 ∣ f (2))$ und berechnest ihre Steigung.

Die Steigung einer Gerade, von der zwei Punkte bekannt sind, kann man mit folgender Formel berechnen: $m=\dfrac{y_B-y_A}{x_B-x_A}$

Hier: $m=\frac{f(2)-f(1)}{2-1}=\frac{2^2+2-2-(1^2+1-2)}{2-1}=\frac{4-0}{2-1}=\frac 4 1 = 4$

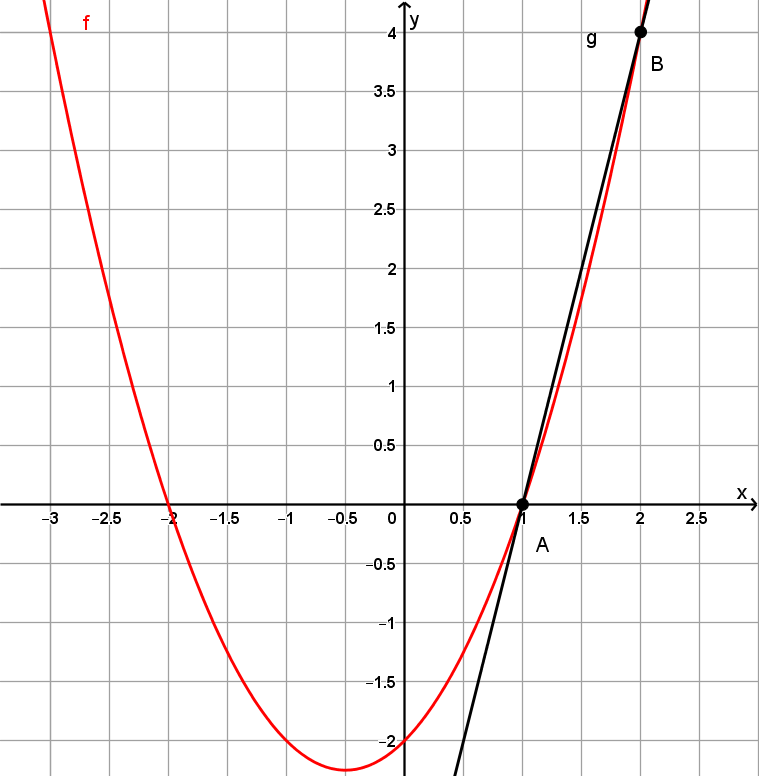
Diese Berechnung nennt man auch Differenzenquotient. Allgemein gilt für den Differenzenquotienten bei einer Funktion $f$ und zwei beliebigen x-Werten $a$ und $b$ : $m=\dfrac{f(b)-f(a)}{b-a}$

6 Aufgaben zu Differenzenquotient

Laden

7 Das Beispiel weiter

Während Patrick seine Messungen vorgenommen hat, ist eine Frau zu ihm gekommen, die sich als Veronika vorstellt und erklärt, dass sie die Erbauerin der Halfpipe ist. Dazu muss sie sich genau mit der Steigung und Geometrie der Halfpipe beschäftigen, weshalb sie sich bereit erklärt Patrick ein wenig zu erklären.

"Wie du die Steigung bestimmt hast, war ein guter Anfang. Du hast bereits gemerkt, dass du Stäbe kleiner machen musst um eine genauere Steigung zu erhalten."

Sie zeigt auf eine Halfpipe die sich noch im Bau befindet und auf den ersten Blick glatt aussieht. "Schau sie dir näher an. Wenn du nah genug ran gehst, merkst du, dass die Bahn nur aus der Enfernung glatt wirkt und eigentlich aus verschiedenen Brettern besteht, welche zur Halfpipe zusammen gebaut wurden. Von jedem einzelnen Brett kannst du die Steigung mithilfe von Anfangs- und Endpunkt bestimmen. Um immer glattere Halfpipes zu bekommen, müssen wir auch immer schmalere Bretter verwenden."

8 Vom Differenzenquotient zum Differentialquotienten

Der Vorgang, der dahinter steckt, dass die Bretter immer schmäler und schmäler werden, ist ein Grenzwertprozess, wie wir ihn zum Beispiel auch haben, wenn wir das Verhalten von Funktionen im Unendlichen oder an Definitionslücken untersuchen.

Allerdings nähern wir uns hier nicht einer bestimmten Zahl x an, also einer Polstelle oder der Unendlichkeit, sondern wir wollen, dass die Differenz zwischen unseren beiden x-Werten verschwindend klein wird, unser Differenzenquotient also immer genauer.