1 Übersicht
In diesem Kurs lernst du die Geosynchrone Umlaufbahn kennen. Satelliten auf dieser Bahn benötigen die gleiche Zeit für einen Umlauf wie die Erde für eine Umdrehung. Dies ist z.B. die Voraussetzung dafür, vom Satellit aus immer den gleichen Blick auf die Erde zu haben. Das ermöglicht die TV-Satelliten-Übertragung und die Erfassung von Wetterdaten.
Vorwissen
Zentripetalkraft
Gravitationskraft
Kursdauer
ca. 60 min
2 Einführung
Körper bewegen sich nach dem Trägheitsgesetz (1. Newtonsches Gesetz) immer mit gleichbleibender Geschwindigkeit geradeaus, falls sie nicht von einer äußeren Kraft beschleunigt / abgelenkt werden. Auf einer Kreisbahn ändert ein Körper dauernd seine Richtung, er muss also dauernd durch eine Kraft beschleunigt werden. Man spricht auch von einer Beschleunigung, wenn sich „nur“ die Richtung der Geschwindigkeit ändert.
Bildquelle: Tobias Rütten, Metoc, CC BY-SA 2.5, Wikimedia
Diese Kraft nennt man Zentripetalkraft. Sie zeigt immer Richtung Mittelpunkt des Kreises. Es gilt:
mit = Masse des Körpers, = Geschwindigkeit des Körpers, = Radius der Kreisbahn.
Als zweites benötigen wir das Gravitationsgesetz, das die Anziehungskraft zweier Massen und beschreibt. Es gilt:
mit der Gravitationskonstante
und dem Abstand der Massenschwerpunkte.
3 Satellitenbahn
Satelliten sind Körper, die sich um die Erde bewegen.
Um die Höhe über dem Erdmittelpunkt einzuhalten, muss ein Satellit eine bestimmte Geschwindigkeit besitzen. Wenn sich die Höhe nicht ändern soll, müssen Gravitationskraft und Zentrifugalkraft gleich groß sein.

Hubble-Weltraum-Teleskop Bildquelle: NASA, public domain, Wikimedia
| ↓ | Formeln einsetzen | ||
| ↓ | | Wurzel ziehen | ||
| ↓ | (ohne negative Lösung) | ||
Diese Gleichung nennen wir . Mit dieser Geschwindigkeit bleibt ein Satellit auf konstanter Höhe. Das ist schon mal eine Eigenschaft, die ein Satellit auf einer geosynchronen Bahn haben muss. Was fehlt jetzt noch?
4 Geosynchrone Umlaufbahn
Wir müssen nun die Umlaufdauer mit ins Spiel bringen. Sie spielt wie der Name geosynchron verrät, eine große Rolle.
Für die Geschwindigkeit bei einer Kreisbewegung mit dem Radius gilt:
Das ist die zweite Bedingung für die Geschwindigkeit des Satellits auf einer geosynchronen Bahn.
Wenn du Gleichung und gleichsetzt, erhälst du die Höhe eines Satelliten, der sich mit der Umlaufdauer um die Erde dreht.
| ↓ | beide Seiten quadrieren | ||
| ↓ | | | ||
| ↓ | | | ||
| ↓ | dritte Wurzel ziehen | ||
Diese relativ komplizierte Formel beschreibt die Höhe über dem Erdmittelpunkt für alle Satelliten mit der Umlaufdauer .
Die dritte und letzte Bedingung für einen Satellit auf einer geosynchronen Bahn ist nun, dass die Umlaufdauer genau 1 Tag beträgt. Dann dauert der Umlauf des Satellits genau so lange wie die Umdrehungsdauer der Erde. Die Zeiten sind synchron.
Wie hoch ist denn jetzt eine geosynchrone Umlaufbahn?
5 Berechnung der Höhe
Wenn wir in die Gleichung die bekannten Größen einsetzen, erhalten wir die gesuchte Höhe.
Gravitationskonstante
Erdmasse
Umlaufdauer
Versuche es selbst mit deinem Taschenrechner. Dort kannst du die Einheiten natürlich weglassen.
Die geosynchrone Bahn befindet sich in einer Höhe von 42.200 km über dem Erdmittelpunkt. Da die Erde einen mittleren Radius von 6378 km hat, ergibt sich für die Höhe über der Erdoberfläche
Bemerkung:
Wenn man die Höhe weiß, kann man mit Gleichung die Geschwindigkeit eines Satellits auf der geosynchronen Bahn berechnen. Versuche es selbst.
Geostationäre Umlaufbahn
Die geostationäre Umlaufbahn ist ein Speziallfall der geosynchronen Umlaufbahn. Der Satellit benötigt für einen Umlauf nicht nur genau einen Tag, er befindet sich dabei auch immer über genau dem gleichen Ort auf der Erde. Dies ist natürlich nur über dem Äquator möglich (Bahnneigung 0°). In diesem Bild schaut man also von oben auf die Drehachse der Erde:
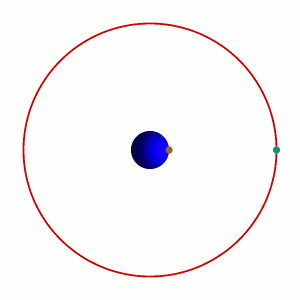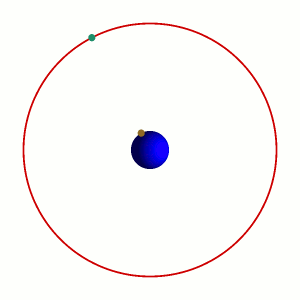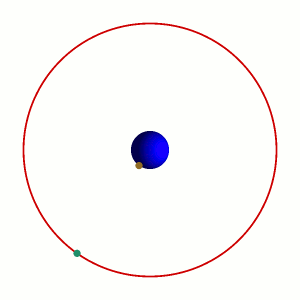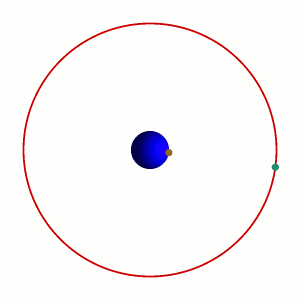
Ein geostationärer Satellit befindet sich immer über dem gleichen Punkt der Erde.
Bildquelle: Brandir, CC BY-SA 3.0, Wikimedia
Satelliten auf einer geostationären Bahn haben somit ...

1.) ... immer den gleichen Blick auf die Erde => Einsatz als Wettersatellit wie z.B. Meteosat
Bildquelle: EUMETSAT, CC BY, Wikimedia

2.) ... von der Erde aus immer die gleiche Position. => Satellitenschüsseln für's Satellitenfernsehen können immer in die gleiche Richtung zeigen.
Bildquelle: © Cody Logan / Wikimedia Commons / "DISH 1000+" / CC BY-SA 4.0
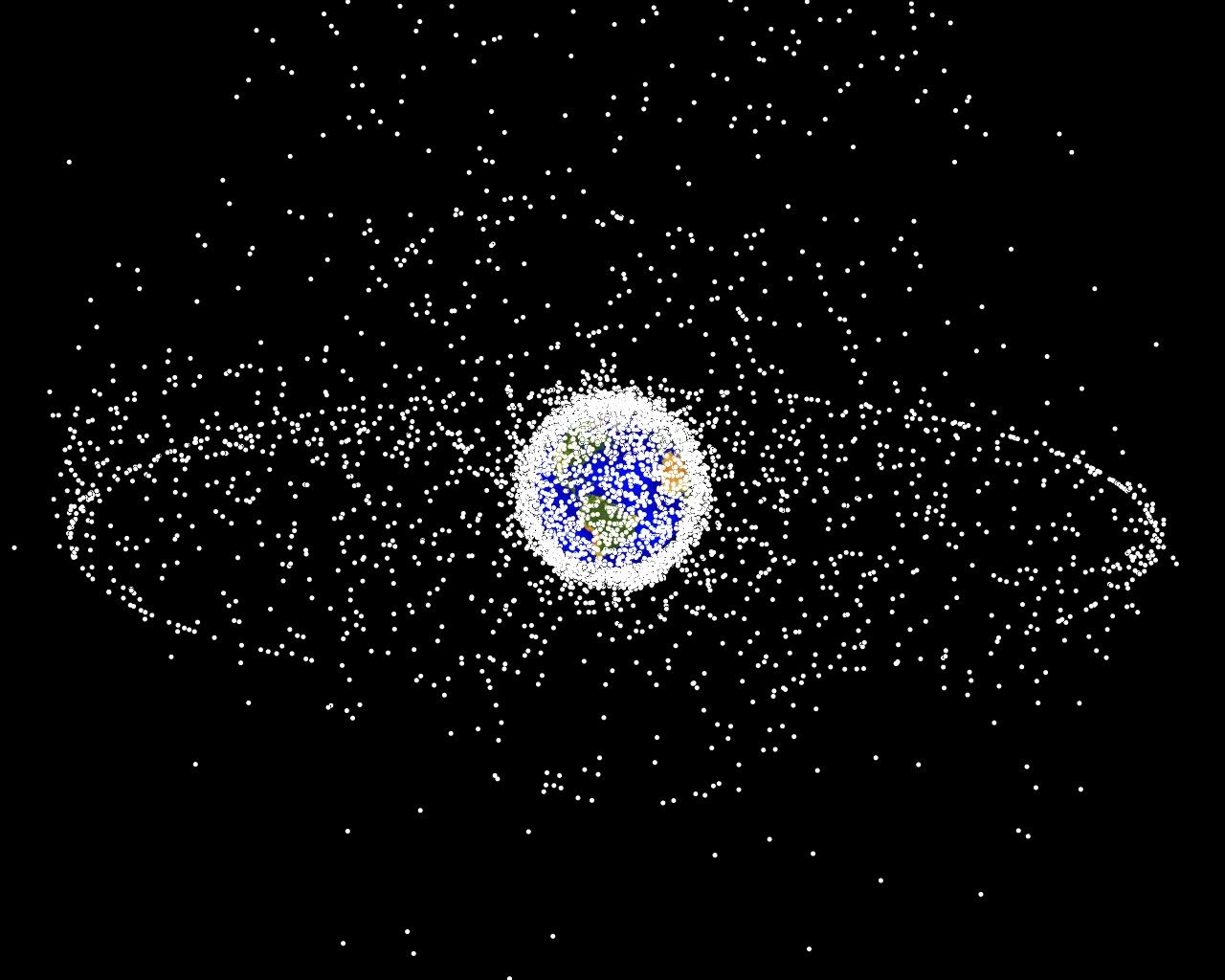
Bildquelle: NASA, public domain, Wikimedia
Diese Computergrafik zeigt alle Satelliten um die Erde. Man sieht innen die meisten Satelliten auf einem Low Earth Orbit, aber auch sehr viele auf einer geostationären Bahn (äußere Linie) über dem Äquator.
Jetzt bist du bereit für die folgenden Aufgaben.
6 Aufgaben
Satellitengeschwindigkeit
Je niedriger ein Satellit fliegt, desto ... muss seine Geschwindigkeit sein.
Globale Navigationssysteme
Zur Positionsbestimmung wurden seit den 1990er-Jahren viele Satelliten gestartet; z.B. das GPS-System. Sie fliegen mit einer Geschwindigkeit von . Berechne ihren Abstand zum Erdmittelpunkt.
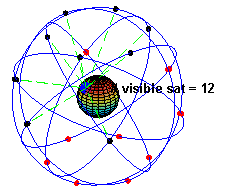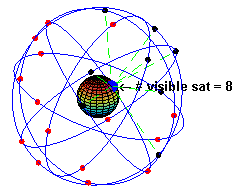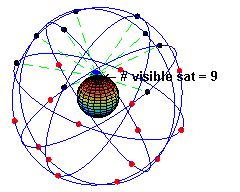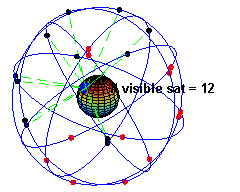
Bildquelle: El pak, public domain, Wikimedia
Berechnung der Sonnenmasse
Die Erde ist eigentlich auch nichts anderes als ein „Satellit“ der Sonne.
Auch hier gilt .
Berechne mit dieser Formel die Sonnenmasse, wenn
und der Abstand zwischen Erde und Sonne
= 1 AE (Astronomische Einheit) 150 Millionen km = beträgt.
