
Die Keplerschen Gesetze beschreiben, wie sich die Planeten um die Sonne bewegen.
1. Planeten bewegen sich auf Ellipsenbahnen um die Sonne.
2. Die Verbindungslinie von Sonne und Planet überstreicht in gleichen Zeiten gleiche Flächen.
3.
1. Keplersches Gesetz
Alle Planeten bewegen sich auf Ellipsenbahnen um die Sonne. Die Sonne befindet sich dabei in einem der beiden Brennpunkte der Ellipsenbahn.
Was ist eine Ellipse?
Eine Ellipse kannst du dir wie einen abgeplatteten Kreis vorstellen. Bei einem Kreis ist der Radius konstant. Ein Kreis ist also genauso "breit" wie "hoch". Bei einer Ellipse hingegen unterscheiden sich die Breite und die Höhe.
Große und kleine Halbachse
Die "halbe Breite" der Ellipse nennt man große Halbachse. Sie wird mit dem Buchstaben bezeichnet und vom Mittelpunkt der Ellipse aus gemessen. Die "Gesamtbreite" der Ellipse beträgt also .
Die "halbe Höhe" der Ellipse heißt kleine Halbachse , weil sie kürzer als die große Halbachse ist. Sie wird mit dem Buchstaben bezeichnet und ebenfalls vom Mittelpunkt aus gemessen. Die "Gesamthöhe" der Ellipse beträgt also .
Wenn und gleich lang sind, dann geht die Ellipse in einen Kreis über. Planeten bewegen sich auf elliptischen Bahnen um die Sonne.
Brennpunkte und Exzentrizität
Ein Kreis besitzt einen Mittelpunkt. Eine Ellipse hingegen hat neben dem Mittelpunkt auch noch zwei Brennpunkte und . Diese legen fest, wie breit die Ellipse ist. Die beiden Brennpunkte sind gleich weit vom Mittelpunkt der Ellipse entfernt. In einem dieser beiden Brennpunkte befindet sich die Sonne.
Der Abstand vom Mittelpunkt zu einem Brennpunkt heißt Exzentrizität .
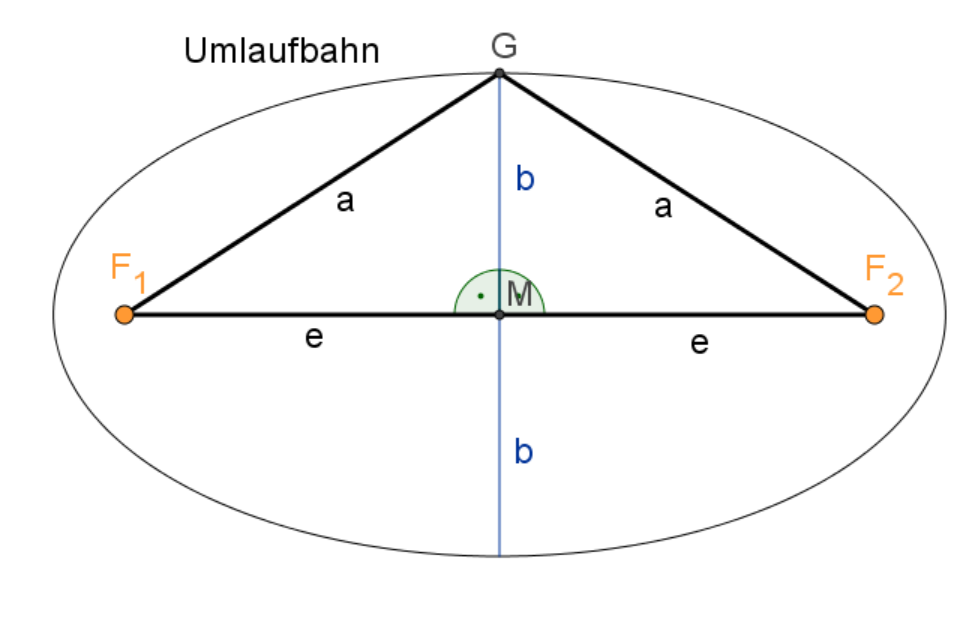
Mit dem Satz des Pythagoras können wir berechnen:
Je weiter die beiden Brennpunkte auseinander liegen, desto "ovaler" wird die Ellipse. Ein Maß für wie stark eine Ellipse vom Kreis abweicht, ist die sogenannte numerische Exzentrizität . Die numerische Exzentrizität liegt zwischen und und hat keine Einheit. Ein Kreis hat eine Exzentrizität von . Je höher die Exzentrizität ist, desto "ovaler" ist die Ellipse.
So kannst du die numerische Exzentrizität berechnen:
Beispiel
Die große Halbachse der Erdumlaufbahn um die Sonne beträgt . Die Erdumlaufbahn hat eine numerische Exzentrizität von .
Wir wollen die kleine Halbachse und die Exzentrizität berechnen.
Für die Exzentrizität stellen wir die Formel nach um. Dafür multiplizieren wir mit :
Jetzt setzen wir unsere Werte ein:
Die kleine Halbachse können wir mit der Formel berechnen. Zuerst stellen wir die Formel nach um.
Wir setzen unsere Werte ein:
Wenn du die kleine und die große Halbachse miteinander vergleichst, fällt dir auf, dass die beiden fast gleich groß sind. In der Tat ist die Erdumlaufbahn fast kreisförmig.
Bemerkung
In der Astrophysik wird oftmals nicht mit Metern oder Kilometern gerechnet, sondern mit sogenannten Astronomischen Einheiten. Diese Einheit wird mit AE, AU oder au (astronomical unit) abgekürzt. Eine Astronomische Einheit entspricht genau der großen Halbachse der Erdumlaufbahn:
2. Keplersches Gesetz
Die Verbindungslinie zwischen der Sonne und einem Planeten überstreicht in gleichen Zeiten gleiche Flächen.
In Gedanken verbindest den Planeten durch eine Linie mit der Sonne. Wenn sich der Planet nun um die Sonne bewegt, dann überstreicht diese Linie eine Fläche - ähnlich wie der Zeiger einer Uhr. Wenn wir den Planeten immer gleich lang beobachten, ist diese überstrichene Fläche nach dem 2. Keplerschen Gesetz immer gleich groß.
Am sonnennähsten Punkt seiner Umlaufbahn ist die Verbindungslinie zwischen Planet und Sonne kürzer als die Verbindungslinie am sonnenfernsten Punkt. Um innerhalb der gleichen Zeitspanne dieselbe Fläche überstreichen zu können, muss sich der Planet in der Nähe der Sonne also schneller bewegen als weit von der Sonne weg. Du kannst dir das 2. Keplersche Gesetz daher auch so merken:
Der sonnennähsten Punkt der Umlaufbahn eines Planeten heißt Perihel, der sonnenfernste Punkt heißt Aphel.
Beispiel
Die Erde bewegt sich im Perihel mit . Im Aphel bewegt sie sich hingegen nur mit einer Geschwindigkeit von um die Sonne.
3. Keplersches Gesetz
Dabei ist die große Halbachse von einem Planeten und dessen Umlaufzeit um die Sonne. ist die große Halbachse eines anderen Planeten mit der Umlaufzeit um die Sonne.
Das 3. Keplersche Gesetz setzt die großen Halbachsen und die Umlaufzeiten zweier Planeten in Relation. Beispielsweise ist von einem Planeten aus dem Sonnensystem die große Halbachse und die Umlaufzeit des Planeten um die Sonne gegeben. Zusätzlich ist noch die große Halbachse eines anderen Planeten aus dem Sonnensystem gegeben. Dann kannst du mit der Formel die Umlaufzeit dieses Planeten berechnen.
Beispiele
Berechnung der Umlaufzeit von Jupiter
Aufgabenstellung: Merkur hat eine große Halbachse von und umrundet die Sonne in Tagen einmal. Jupiter hat eine große Halbachse von . Berechne, wie lange Jupiter für einen Umlauf um die Sonne benötigt.
Merkur ist nun unser Planet 1 und Jupiter ist unser Planet 2. Folgendes wissen wir aus der Aufgabenstellung:
. Das steht für die Einheit days, also Tage.
Wir wollen berechnen, also die Umlaufzeit von Jupiter um die Sonne. Dafür stellen wir die Formel nach um:
↓ | steht im Nenner. Deshalb bilden wir die Kehrbrüche auf beiden Seiten der Gleichung, d.h. wir drehen Zähler und Nenner auf beiden Seiten um. | ||
↓ | Damit auf einer Seite alleine stehen kann, multiplizieren wir nun mit | ||
↓ | Nun ziehen wir auf beiden Seiten die Wurzel, um das Quadrat bei wegzubekommen. | ||
Jetzt können wir unsere Werte einsetzen:
Jupiter benötigt also Tage, um die Sonne einmal zu umrunden. Indem wir diese Zahl durch teilen, erhalten wir die Umlaufzeit von Jupiter in Erdjahren:
Jahre
