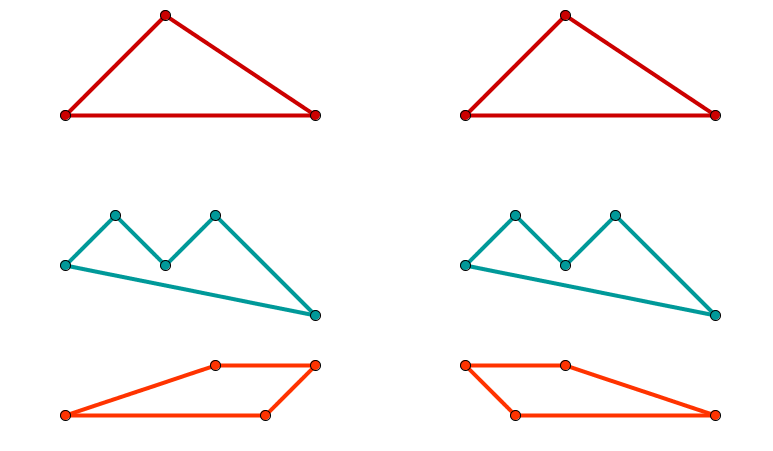
Zwei Figuren heißen kongruent, wenn sie deckungsgleich sind, d. h. wenn sie in entsprechenden Seiten gleich lang und entsprechende Winkel gleich groß sind.
Kongruenzabbildungen
Kongruenzabbildungen sind Abbildungen, bei denen Figur und Bildfigur kongruent sind, d. h. die Figur vor und nach der Abbildung sich nicht in Form und Größe unterscheiden. Es gibt vier Arten von Kongruenzabbildungen:
Verschiebung
Drehung
Meistens werden mehrere dieser Kongruenzabbildungen hintereinander ausgeführt.

Beispiel einer Kongruenzabbildung
Der Vogel wurde gespiegelt, verschoben und gedreht, dennoch sagt man es gibt eine Kongruenzabbildung die den einen Vogel in den anderen überführt.
Die Verknüpfung mehrerer Kongruenzabbildungen ist somit auch eine Kongruenzabbildung.
Zusammensetzung von Spiegelungen
Jede noch so komplizierte Kongruenzabbildung lässt sich durch maximal drei Spiegelungen erzeugen.
Verschiebung
Spiegelt man ein Objekt und Spiegelt das Spiegelbild ein weiters mal an einer dazu parallelen Achse erzeugt man eine verschobene Version des Ursprünglichen Objektes.
Hierbei fällt auf, dass die Position des verschobenen Vogels nur von dem Abstand der parallelen Spiegelebenen (und deren Orientierung) abhängt und nicht von der Position der Ebenen.
Drehung
Spiegelt man an zwei Spiegelachsen die sich schneiden ist das Resultat ein um den Schnittpunkt gedrehter Objekt.
Hierbei fällt auf, dass der Drehwinkel des gedrehten Vogels nur von dem Winkel zwischen Spiegel-Achsen an sich abhängt und nicht von der Positionen der einzelnen Achsen.
Eine Drehung auf der Stelle ist auch möglich wenn sich der Drehpunkt (Schnittpunkt der Spiegelachsen) in dem Bildzentrum befindet.
Kombinationen
Jede Kombination von Kongruenzabbildungen wird erzeugt, indem die Figur entweder zuerst durch eine Spiegelung auf ihre Position gebracht und dann an Ort und Stelle gedreht wird, oder indem die Figur auf die richtige Position verschoben und anschließend an Ort und Stelle gedreht wird.
Wenn man seine Figur spiegelt und dann dreht, benötigt man insgesamt drei Spiegelungen.
Bei der Verschiebung der Figur und anschließender Drehung scheint es, als würde man vier Spiegelungen benötigen. Tatsächlich sind jedoch nur zwei notwendig.
Beim Verschieben kann die Position der zweiten Spiegelebene frei gewählt werden, solange der Abstand der Spiellachsen (und deren Orientierung) korrekt ist. Beim Drehen der Figur kann die Orientierung der ersten Achse nach Belieben gewählt werden, solange der Winkel (und Schnittpunkt) zwischen den Achsen übereinstimmt. Auf diese Weise können die zweite Spiegelung der Verschiebung und die erste Spiegelung der Drehung übereinander gelegt werden. Wenn man zweimal an derselben Stelle spiegelt, können auch beide Spiegelungen weggelassen werden.
Kongruente Dreiecke
Die Kongruenz von Dreiecken lässt sich mithilfe der Kongruenzsätze überprüfen.
Kongruenzsätze
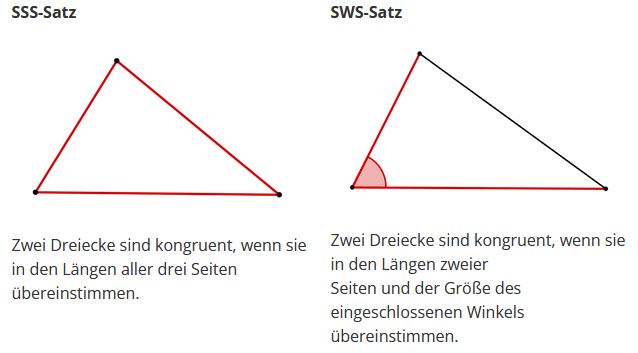
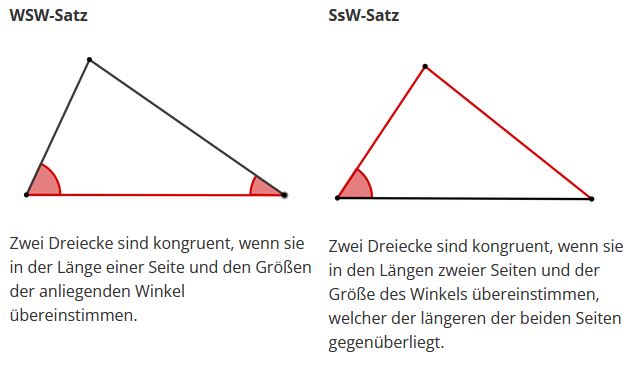
Der WSW-Satz wird manchmal auch als SWW- oder WWS-Satz bezeichnet, da man bei zwei bekannten Winkeln, aufgrund der Innenwinkelsumme, den Dritten ausrechnen kann. Somit findet man bei zwei gegebenen Winkel und einer Seite immer die beiden Winkel, die an dieser Seite anliegen.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kongruenz und Ähnlichkeit von Dreiecken
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
