1 Übersicht
In diesem Kurs lernst du den Dijkstra-Algorithmus und eine mögliche Anwendung davon kennen: Finde effiziente Wege durch ein Straßennetz mit dem Dijkstra-Algorithmus!

Benötigtes Vorwissen:
Graphen (Begriff Knoten, Kante, Kantengewicht)
Bearbeitungszeit:
ca 30 Min
2 Hilfe für den Weihnachtsmann
Um den Weihnachtsmann zu entlasten, bekommt der Wichtel Dijkstra Jr. die Aufgabe, die Dörfer rund um die Werkstatt am Nordpol mit Geschenken zu beliefern.
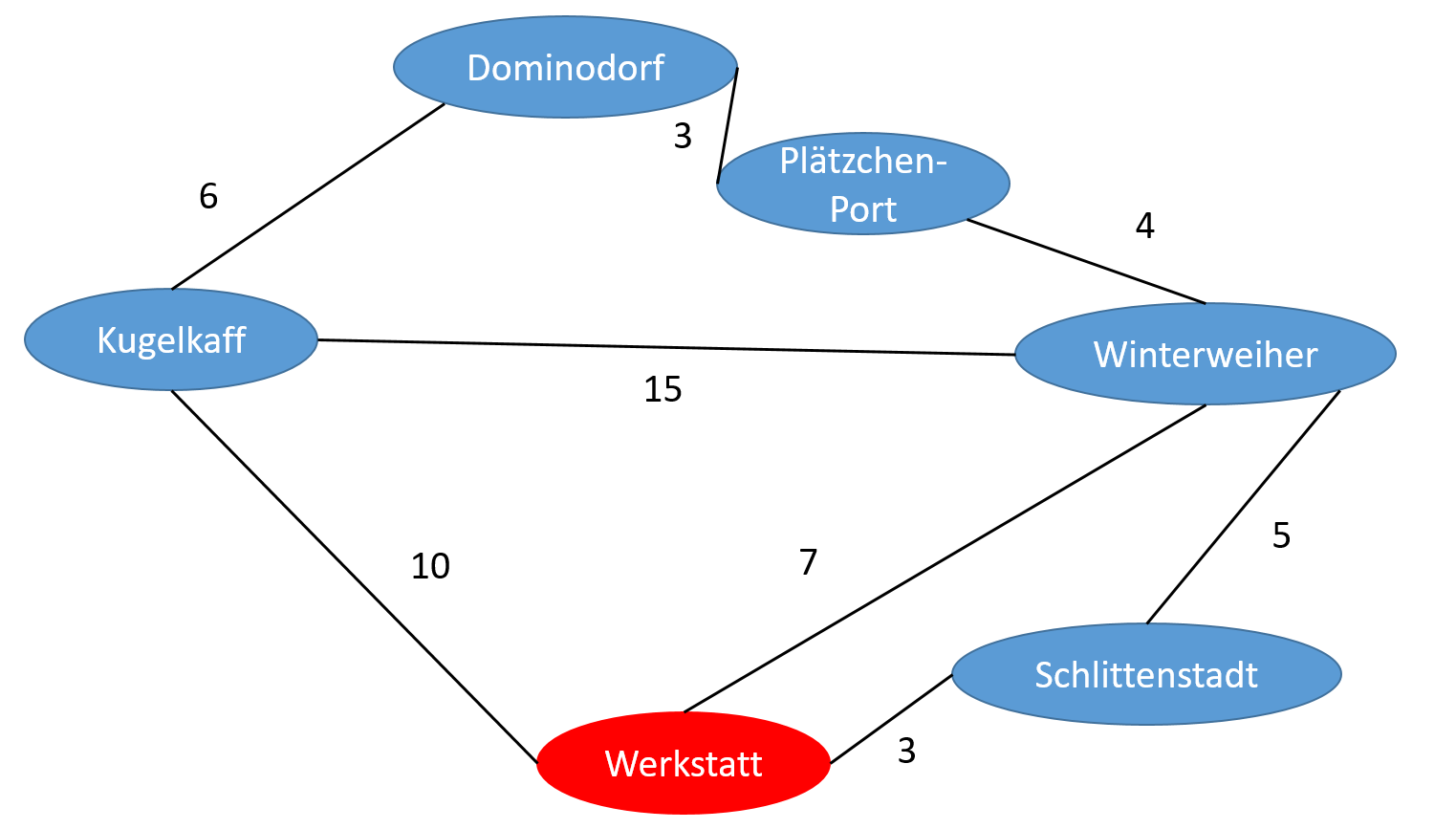
Die Knoten des Graphen stehen auf dieser Karte für die einzelnen Dörfer, die Zahlen an den Kanten sind die Längen der (in der Realität natürlich nicht so geraden) Straßen in Kilometern.
3 Planung von Dijkstra Jr.
Dijkstra Jr. hat ein paar Freunde versammelt, die ihn unterstützen sollen und macht sich mit ihnen an die Routenplanung.
Sein Ziel: Für jedes Gebiet in der Nachbarschaft möchte er den kürzesten Weg von der Weihnachtswerkstatt dorthin finden, um so effiziente Routen zu planen.
Überlegung: Bevor du einen Algorithmus kennenlernst, der dieses Problem auch für sehr große Graphen lösen kann, kannst du für dieses einfache Beispiel selbst eine Lösung finden. Notiere dir für jedes Dorf im Graphen den kürzesten Weg von der Werkstatt zu diesem Ort.
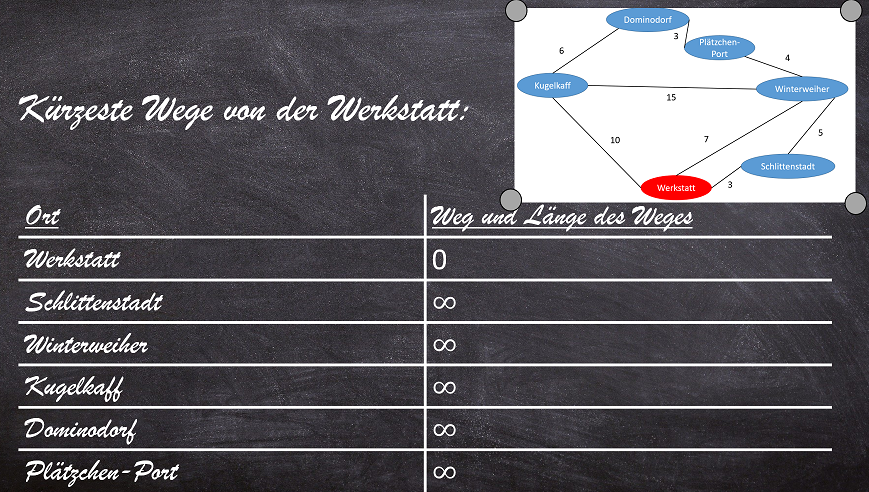
4 Vorbereitung Dijkstra-Algorithmus
Dijkstra Jr. benutzt den bekannten Familien-Algorithmus, den Dijkstra-Algorithmus, um die kürzesten Wege zu bestimmen. Du hilfst ihm dabei.

Vorbereitung
Schreibe in eine Tabelle alle Knoten des Graphen (alle Städte) und lege als Startdistanz für alle Städte außer für den Ausgangspunkt den Wert unendlich fest.
Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Nein | 0 | - |
Schlittenstadt | Nein | ||
Kugelkaff | Nein | ||
Winterweiher | Nein | ||
Dominodorf | Nein | ||
Plätzchen-Port | Nein |
5 Distanz senken und nächsten Ort heraussuchen
Zunächst kannst du für jeden Ort, der direkt mit der Werkstatt verbunden ist, die Distanz von , auf die angegebenen km senken und diesen Ort als abgehandelt markieren. In diesem ersten Schritt sind alle Distanzen automatisch kürzer als die zuerst festgelegte und du musst deshalb nichts nachrechnen oder überprüfen.
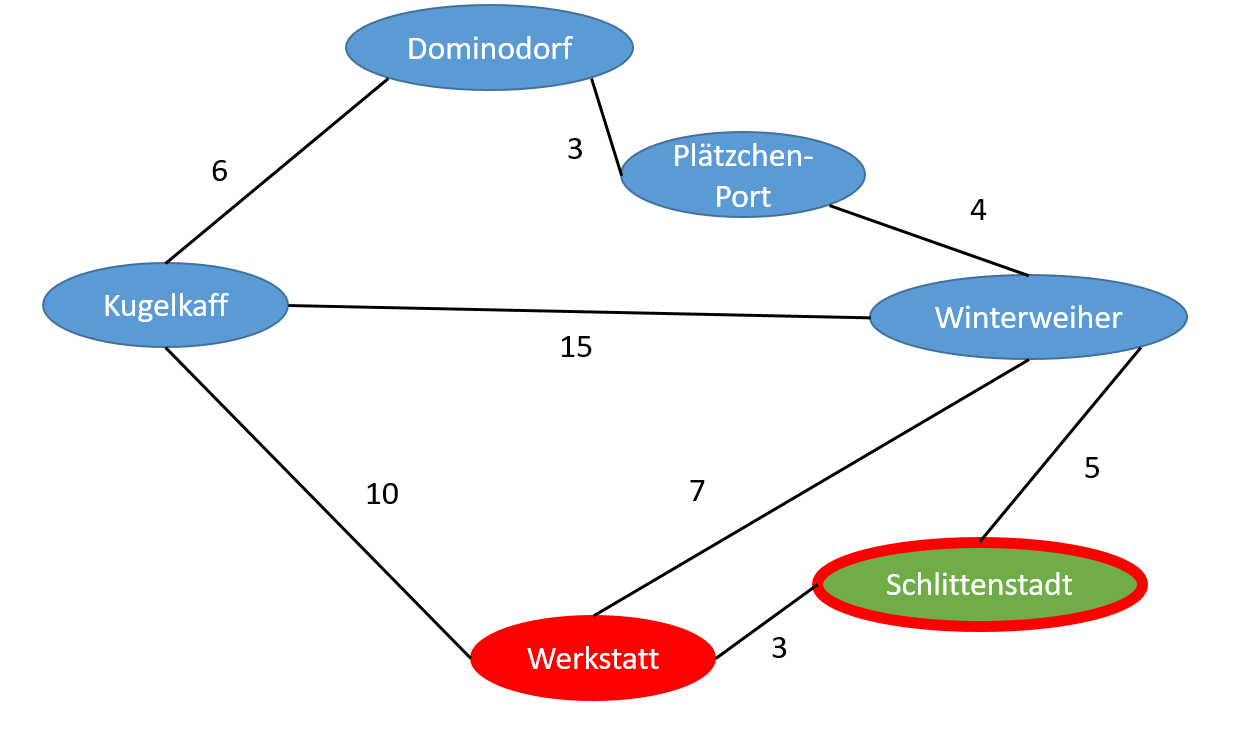
Anschließend suchst du unter den gerade markierten Orten das Dorf heraus, das die kürzeste Distanz zum Startknoten (also der Werkstatt) hat und noch nicht besucht wurde. Dieser Ort ist Schlittenstadt. Markiere ihn als neuen aktuellen Knoten (rot umrandet in Grafik, fett in Tabelle).
Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt, abgehandelt) | Ja | 0 | - |
Schlittenstadt (aktueller Ort) | Nein | 3 | Werkstatt |
Kugelkaff | Nein | 10 | Werkstatt |
Winterweiher | Nein | 7 | Werkstatt |
Dominodorf | Nein | ||
Plätzchen-Port | Nein |
6 Nächsten Ort untersuchen
Vom aktuellen Ort werden wieder alle erreichbaren Orte untersucht. Falls die Distanz kleiner ist als die aktuell eingetragene, wird die Tabelle verändert.
Da der Weg nach Winterweiher über Schlittenstadt mit 8 km (3km +5km) länger ist als die Straße von der Werkstatt aus (7 km), verändert sich nichts in der Tabelle.
Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Ja | 0 | - |
Schlittenstadt (aktueller Ort) | Ja | 3 | Werkstatt |
Kugelkaff | Nein | 10 | Werkstatt |
Winterweiher | Nein | 7 | Werkstatt |
Dominodorf | Nein | ||
Plätzchen-Port | Nein |

7 Nächsten Ort heraussuchen
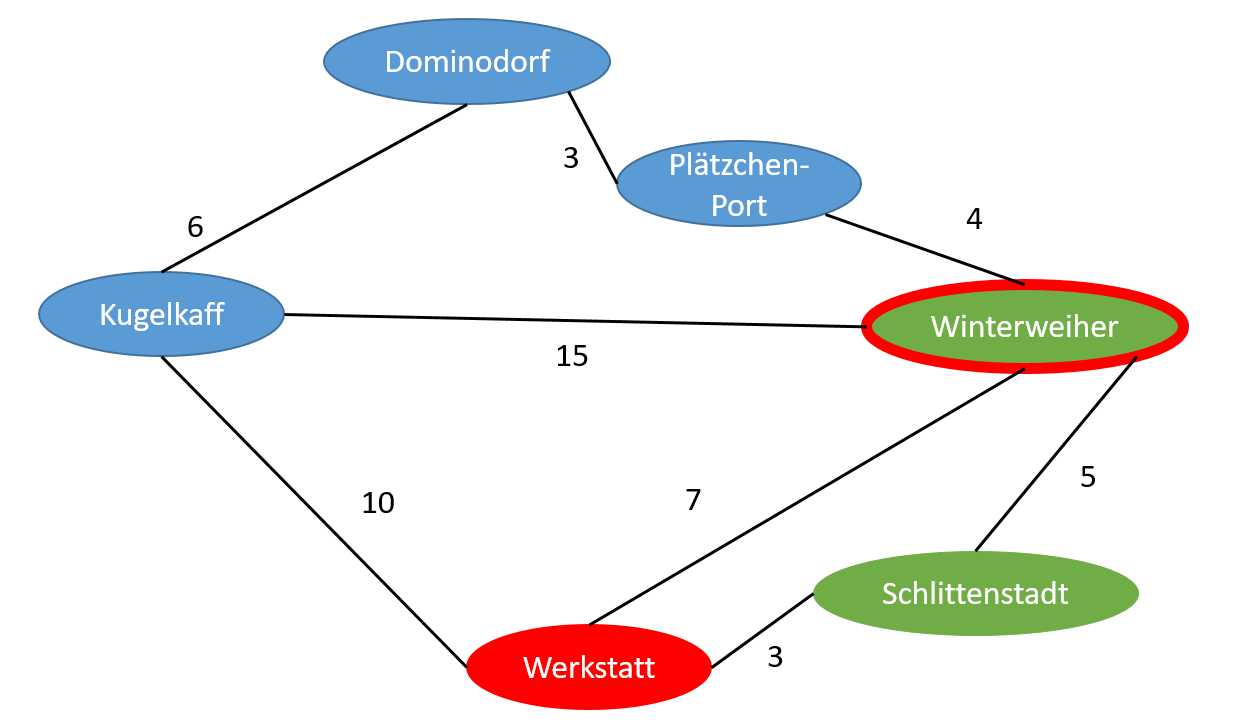
Wähle aus der Tabelle den Ort aus, der die kleinste Distanz zum Startort hat und noch nicht untersucht wurde. Dieser Ort ist Winterweiher. Markiere ihn als aktuellen Ort:
Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Ja | 0 | - |
Schlittenstadt | Ja | 3 | Werkstatt |
Kugelkaff | Nein | 10 | Werkstatt |
Winterweiher (aktueller Ort) | Nein | 7 | Werkstatt |
Dominodorf | Nein | ||
Plätzchen-Port | Nein |
8 Nächsten Ort untersuchen
Von Winterweiher aus können Kugelkaff und Plätzchen-Port erreicht werden.
Die Route nach Kugelkaff ist allerdings mit 22 km länger als die bisherige (10 km).
Die Route nach Plätzchen-Port ist kürzer und wird deshalb in der Tabelle vermerkt:

Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Ja | 0 | - |
Schlittenstadt | Ja | 3 | Werkstatt |
Kugelkaff | Nein | 10 | Werkstatt |
Winterweiher (aktueller Ort) | Ja | 7 | Werkstatt |
Dominodorf | Nein | ||
Plätzchen-Port | Nein | 11 | Winterweiher |
9 Nächsten Ort aussuchen
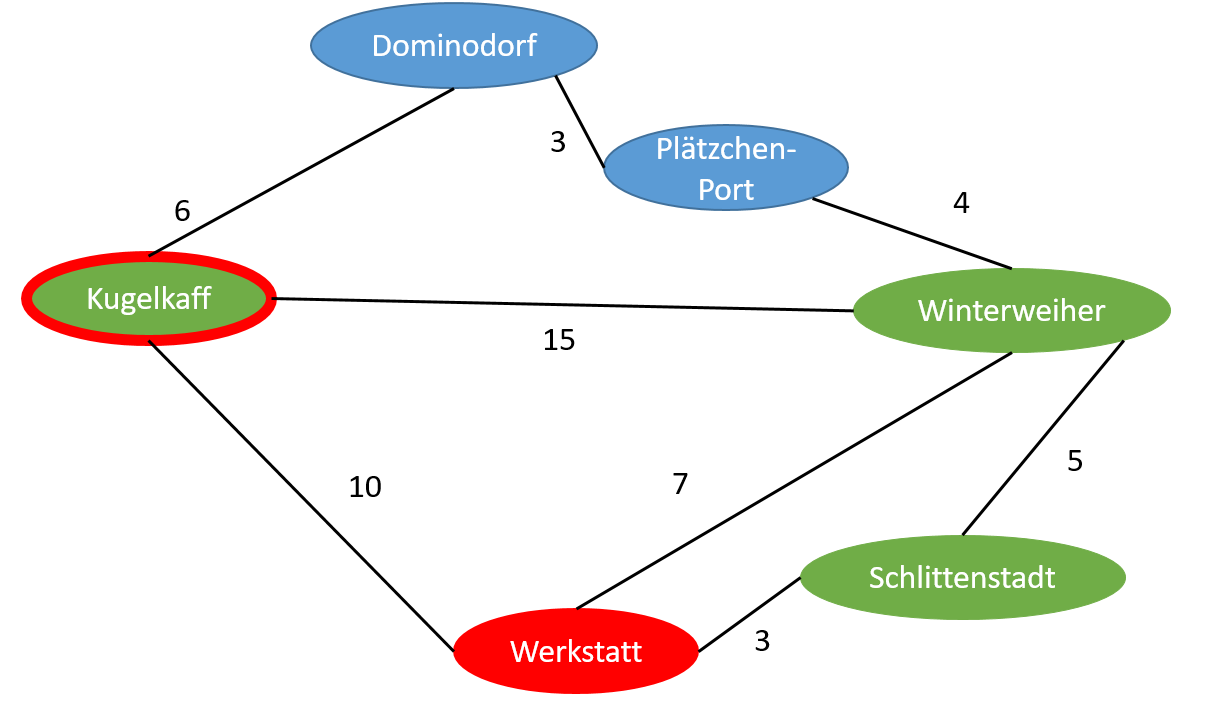
Wähle aus der Tabelle den Ort aus, der die kleinste Distanz zum Startort hat und noch nicht untersucht wurde. Dieser Ort ist Kugelkaff. Markiere ihn als aktuellen Ort:
Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Ja | 0 | - |
Schlittenstadt | Ja | 3 | Werkstatt |
Kugelkaff (aktueller Ort) | Nein | 10 | Werkstatt |
Winterweiher | Ja | 7 | Werkstatt |
Dominodorf | Nein | ||
Plätzchen-Port | Nein | 11 | Winterweiher |
10 Nächsten Ort untersuchen
Der Weg von Kugelkaff nach Winterweiher ist länger (25 km) als der bisher gefundene (7km).
Der Weg nach Dominodorf wird mit 16 km in der Tabelle ergänzt.

Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Ja | 0 | - |
Schlittenstadt | Ja | 3 | Werkstatt |
Kugelkaff (aktueller Ort) | Ja | 10 | Werkstatt |
Winterweiher | Ja | 7 | Werkstatt |
Dominodorf | Nein | 16 | Kugelkaff |
Plätzchen-Port | Nein | 11 | Winterweiher |
11 Nächsten Ort aussuchen
Jetzt hast du zwar zu jedem Dorf einen Weg gefunden, dieser muss aber nicht der kürzeste sein! Du musst alle Knoten einmal untersucht haben, damit der Dijkstra-Algorithmus das gesuchte Ergebnis liefert.
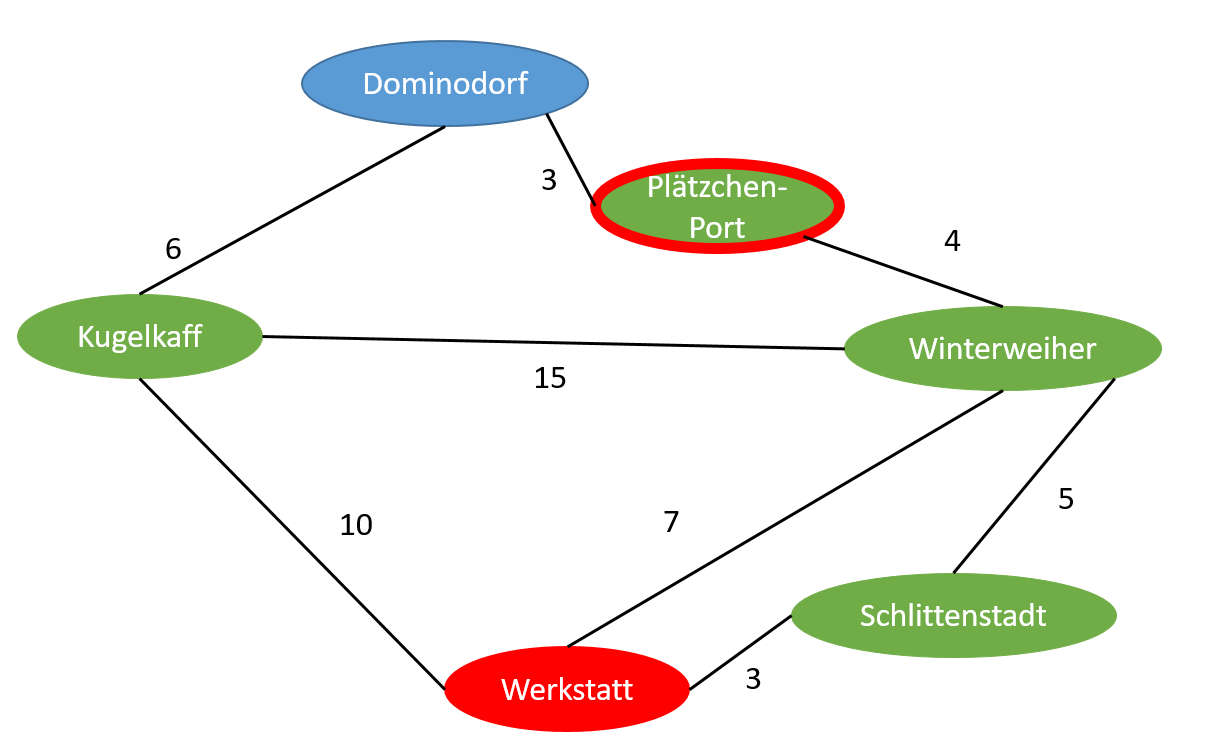
Wähle deshalb erneut aus der Tabelle den Ort aus, der die kleinste Distanz zum Startort hat und noch nicht untersucht wurde. Dieser Ort ist Plätzchen-Port. Markiere ihn als aktuellen Ort:
Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Ja | 0 | - |
Schlittenstadt | Ja | 3 | Werkstatt |
Kugelkaff | Ja | 10 | Werkstatt |
Winterweiher | Ja | 7 | Werkstatt |
Dominodorf | Nein | 16 | Kugelkaff |
Plätzchen-Port (aktueller Ort) | Nein | 11 | Winterweiher |
12 Nächsten Ort untersuchen
Der Weg nach Dominodorf von Plätzchen-Port aus ist um 1 km kürzer als von Kugelkaff aus. Die Tabelle wird entsprechend aktualisiert.

Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Ja | 0 | - |
Schlittenstadt | Ja | 3 | Werkstatt |
Kugelkaff | Ja | 10 | Werkstatt |
Winterweiher | Ja | 7 | Werkstatt |
Dominodorf | Nein | 14 | Plätzchen-Port |
Plätzchen-Port (aktueller Ort) | Ja | 11 | Winterweiher |
13 Letzten Ort untersuchen und Routen ableiten
Auch Dominodorf muss noch untersucht werden. Allerdings verändern sich die Wege dadurch nicht: Nach Kugelkaff wären es 20 km, nach Plätzchen-Port 17 km.
Die finalen Distanzen zwischen der Werkstatt und allen Städten sehen also wie folgt aus:
Ort | Abgehandelt | Distanz | Vorgänger |
|---|---|---|---|
Werkstatt (Startpunkt) | Ja | 0 | - |
Schlittenstadt | Ja | 3 | Werkstatt |
Kugelkaff | Ja | 10 | Werkstatt |
Winterweiher | Ja | 7 | Werkstatt |
Dominodorf | Ja | 14 | Plätzchen-Port |
Plätzchen-Port | Ja | 11 | Winterweiher |
Beachtet man die Vorgänger, ergeben sich daraus folgende Routen:
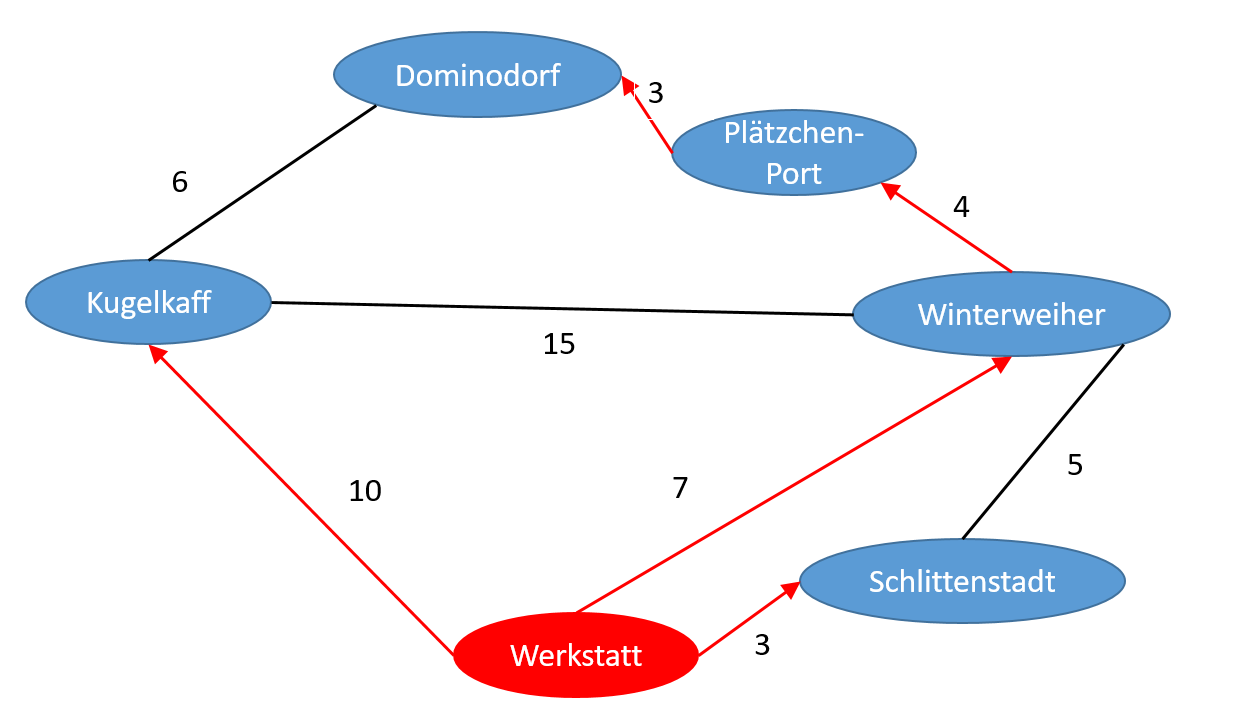
14 Ablauf auf einen Blick
Beim Vorgehen von Dijkstra Jr. handelt es sich um einen Algorithmus. Das heißt, er lässt sich zum Beispiel mithilfe eines Struktogramms übersichtlich beschreiben und darstellen. Alle Handlungen, die du in den letzten Schritten mit den Wichteln durchgeführt hast, lassen sich "formal" so aufschreiben:

15 Abschließende Übung
Laden
