Wie gehst du vor, wenn du ein algorithmisches Problem lösen willst?
Beispielsweise bist du Handelsvertreter und möchtest die kürzeste Rundreise durch alle Großstädte Deutschlands herausfinden. Dies ist das berühmte Travelling Salesman Problem (TSP) oder Problem des Handlungsreisenden.
Problem
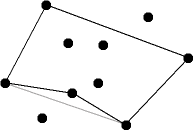
In der Abbildung rechts siehst du eine Landkarte mit 10 Städten. Deine Aufgabe: Starte in einer Stadt, besuche alle Städte genau einmal und kehre dann zur Ausgangsstadt zurück. Das ist an sich kein Problem - aber: Du sollst dabei den kürzestmöglichen Weg zurücklegen.
Diese kürzestmögliche Rundreise durch alle 10 Städte siehst du hier. Wie aber findest du diese kürzeste Rundreise? Und vor allem: Wie findest du die kürzeste Rundreise, wenn es 100 Städte sind?

Strategien
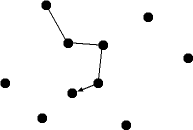
Eine mögliche Strategie ist: Du fährst immer zur nächstgelegenen Stadt, in der du noch nicht gewesen bist, und ganz zum Schluss wieder zurück zu deinem Ausgangsort.
Dies ist die Greedy-Strategie (engl. greedy– gierig). Aber nicht immer ist die Strategie "Nimm was du kriegen kannst" die beste – manchmal ist es besser, sich zunächst zurückzuhalten, um später umso reichlicher belohnt zu werden.
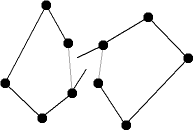
Oder du wendest die Divide-and-Conquer-Strategie an. Divide and conquer bedeutet teile und herrsche: Du beherrscht ein kleineres Problem leichter als ein großes.
Du teilst die Städte in zwei Gebiete ein (divide).
Du berechnest für die Städte jedes Gebiets die kürzeste Rundreise (conquer)
Du verbindest diese Rundreisen an der nächstgelegenen Stelle zu einer Rundreise (combine).
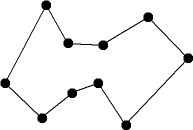
Oder du entscheidest dich für die Strategie Dynamische Programmierung. Du startest mit einer Rundreise durch 4 Städte: die nördlichste, die östlichste, die südlichste und die westlichste Stadt.
Dann fügst du die restlichen Städte eine nach der anderen in diese Rundreise ein, immer diejenige zuerst, die am wenigsten Umweg verursacht.
Anhand des Travelling-Salesman-Problems lassen sich diese algorithmischen Strategien gut veranschaulichen – allerdings: Sie funktionieren bei diesem Problem alle nicht!
Bei anderen Problemen jedoch sehr wohl, du lernst in den Artikeln hier in diesem Bereich einige kennen.
Eine Strategie, die bei diesem Problem auch nicht funktioniert, ist die Transformation in ein anderes Problem. Es stellt sich heraus, dass jedes solche andere Problem mindestens genauso schwer zu lösen ist.
Es bleibt noch die Brute-Force-Strategie, also sozusagen die Anwendung roher Gewalt. Du berechnest einfach alle Rundreisen und suchst die kürzeste aus. Theoretisch funktioniert diese Strategie, aber praktisch ist sie bei einer größeren Anzahl von Städten undurchführbar. Denn bei einer Anzahl von Städten gibt es verschiedene Rundreisen – schon bei 50 Städten sind dies mehr als Rundreisen.
Und es bleiben noch sogenannte heuristische Strategien, die in ziemlich kurzer Zeit ziemlich gute Lösungen finden. Ein paar Kilometer mehr? Und wenn schon. Als Handelsvertreter musst du schließlich irgendwann einmal losfahren und kannst nicht noch wochenlange Berechnungen anstellen.
Schau dir einmal an, bei welchen algorithmischen Problemen du die Divide-and-Conquer-Strategie oder die Dynamische-Programmierungs-Strategie sinnvoll einsetzt.
Aufgaben
Versuche eine möglichst einfache Travelling-Salesman-Problemstellung zu entwerfen, bei der die Greedy-Strategie nicht zur kürzesten Rundreise führt. Arrangiere also vier oder fünf Punkte so auf einem Stück Papier, dass nicht die kürzeste Rundreise herauskommt, wenn du die Punkte nach der Greedy-Strategie ("gehe immer zum nächstgelegenen Punkt") zu einer Rundreise verbindest.
Entwirf eine möglichst einfache Travelling-Salesman-Problemstellung, bei der du mit der Divide-and-Conquer-Strategie nicht die kürzeste Rundreise findest.
Finde eine möglichst einfache Travelling-Salesman-Problemstellung, bei der die Strategie Dynamische Programmierung nicht zur kürzesten Rundreise führt.