Sortierverfahren Mergesort

Das Sortierverfahren Mergesort gehört zu den schnellsten Sortierverfahren. Es ist ein Paradebeispiel für die Anwendung der Divide-and-Conquer-Strategie.

Divide-and-Conquer-Strategie

Oft kannst du ein Problem schneller lösen, indem du es zunächst in zwei kleinere Teilprobleme zerlegst (divide). Dann löst du die Teilprobleme (conquer), und aus diesen Lösungen setzt du die Gesamtlösung zusammen (combine).

Nach diesem Prinzip funktioniert das Sortierverfahren Mergesort.

Sortierverfahren Mergesort

Du willst ein Array $a$ von Daten sortieren. Du unterteilst das Array in zwei Hälften (divide). Dann sortierst du jede Hälfte des Arrays für sich (conquer). Diese beiden sortierten Hälften verschmilzt du dann zu einem insgesamt sortierten Array (combine).

Das Verschmelzen (engl. to merge) der beiden sortierten Hälften geht so: Du kopierst die sortierte vordere Hälfte des Arrays $a$ in ein Hilfsarray $b$ und die sortierte hintere Hälfte in ein Hilfsarray $c$ .

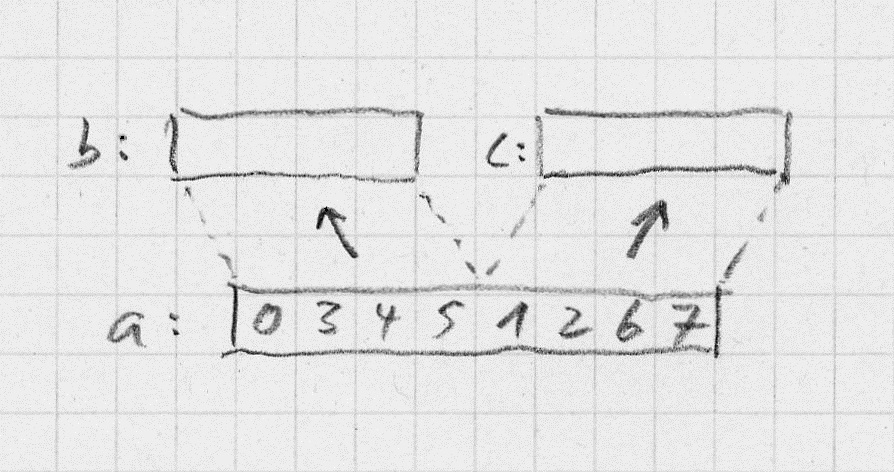
Dann entnimmst du aus diesen beiden Hilfsarrays immer das jeweils nächstgrößere Element und kopierst es der Reihe nach zurück in das ursprüngliche Array $a$ . Die Indexpositionen $i$ , $j$ und $k$ zeigen dir dabei an, wo du gerade bist. Zum Schluss ist das Array $a$ insgesamt sortiert.

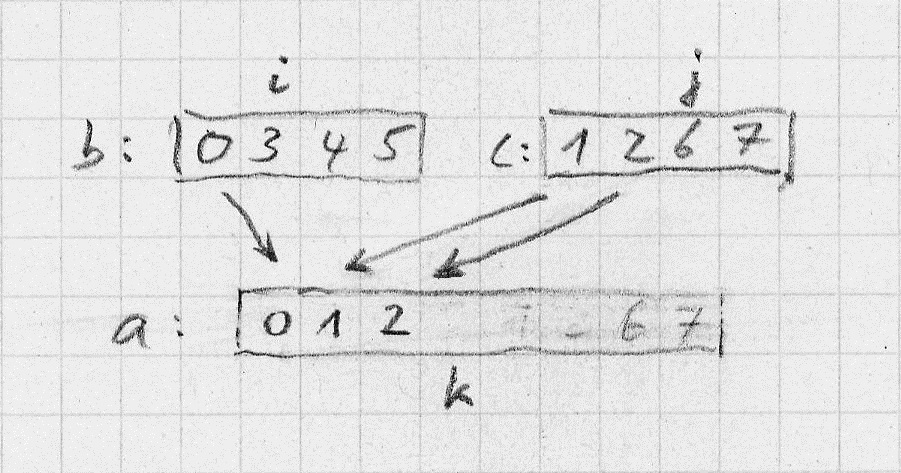
Elemente aus den Hilfsarrays der Größe nach zurückkopieren

Funktion merge

In der Programmiersprache Python sieht die entsprechende Funktion merge folgendermaßen aus:

# Verschmilzt sortiertes vorderes Teilstueck von Array a,
# beginnend beim Index lo bis zum Index m (ausschliesslich),
# mit hinterem sortiertem Teilstueck von Array a,
# beginnend beim Index m bis zum Index hi (ausschliesslich),
# zu einem insgesamt sortierten Teilstueck von Array a,
# beginnend beim Index lo bis zum Index hi (ausschliesslich)
def merge(a, lo, m, hi):
    # Haelften in Hilfsarrays b und c kopieren
    b=a[lo:m]
    c=a[m:hi]

    # Eintraege der Hilfsarrays geordnet nach a zurueckkopieren
    i=0
    j=0
    k=lo
    while i<len(b) and j<len(c):
        if b[i]<=c[j]:
            a[k]=b[i]
            i+=1
        else:
            a[k]=c[j]
            j+=1
        k+=1

    # falls vorhanden Rest des Hilfsarrays b zurueckkopieren
    while i<len(b):
        a[k]=b[i]
        i+=1
        k+=1

    # falls vorhanden Rest des Hilfsarrays c zurueckkopieren
    while j<len(c):
        a[k]=c[j]
        j+=1
        k+=1

Anhand der Abbildungen hast du vielleicht eine Vorstellung davon gewonnen, wie die Funktion merge funktioniert. Probiere einmal selbst mit Karopapier und Bleistift aus, wie die Funktion merge das folgende Array $a$ , das aus zwei sortierten Hälften besteht, zu einem insgesamt sortierten Array verschmilzt.

\displaystyle a=[0, 1, 3, 4, 2, 5, 6, 7]

Du wirst feststellen, dass du den eventuell verbliebenen Rest des Hilfsarrays $c$ gar nicht zurückkopieren musst – warum? Den letzten Absatz der Funktion merge kannst du also weglassen.
Es gibt noch ein paar andere Möglichkeiten, die Funktion merge zu optimieren, hast du Ideen?

Funktion mergesort

Aber bevor du optimierst, schreibe erst noch die Funktion mergesort. Denn du möchtest ja ein komplett unsortiertes Array sortieren. Dies machst du rekursiv:

Du sortierst die vordere Hälfte des Arrays durch einen rekursiven Aufruf der Funktion mergesort.
Du sortierst die hintere Hälfte durch einen weiteren rekursiven Aufruf der Funktion mergesort.
Nun ist alles bereit für den Aufruf der Funktion merge, du rufst sie also auf – fertig!

Das Programm dazu ist folgendes:

# Sortiert ein Teilstueck des Arrays a
# beginnend beim Index lo bis zum Index hi (ausschliesslich)
def mergesort(a, lo, hi):
    if hi-lo>1:
        m=(lo+hi)//2         # m = Index in der Mitte
        mergesort(a, lo, m)  # vordere Haelfte sortieren
        mergesort(a, m, hi)  # hintere Haelfte sortieren
        merge(a, lo, m , hi) # Haelften verschmelzen

Die wichtigste Zeile im Funktionskörper ist die erste Zeile: Du musst sicherstellen, dass die Rekursion irgendwann endet. Dies tut sie dann, wenn ein zu sortierendes Teilstück nur noch aus einem Element besteht.

Beachte bitte eine python-spezifische Besonderheit: Indexbereiche beginnen immer bei einem unteren Index (zum Beispiel lo) und enden immer vor dem genannten oberen Index (zum Beispiel hi).

Rekursion verstehen

Vielleicht fragst du dich: Wie kann denn die Funktion mergesort schon aufgerufen werden, wenn sie noch gar nicht fertig definiert ist?

Doch! Die Funktion ist an dieser Stelle schon fertig definiert! Und zwar für Array-Teilstücke der Länge 1. Denn ein Teilstück, das nur aus einem Element besteht, ist bereits sortiert. Dieser Fall wird durch die nicht erfüllte Bedingung, dass hi-lo>1 ist, erkannt. In diesem Fall macht die Funktion mergesort das einzig Richtige: nichts.

Jedes Mal, wenn du mergesort rekursiv aufrufst, springst du ja wieder in die Funktion hinein, aber jedes Mal mit einem kürzeren zu sortierenden Teilstück des Arrays. Und irgendwann besteht das Teilstück nur noch aus einem einzigen Element. Dann endet die Rekursion.

Im Endeffekt verschmilzt du auf diese Weise zunächst Teilstücke der Länge 1 zu sortierten Teilstücken der Länge 2, diese dann zu sortierten Teilstücken der Länge 4 und so weiter. Jedenfalls dann, wenn die Länge des Arrays eine Zweierpotenz ist.

Aber das Programm funktioniert auch, wenn die Länge des Arrays eine beliebige Zahl ist. In diesem Fall werden auch Teilstücke, deren Länge sich um 1 unterscheidet, miteinander verschmolzen.

Programm ausprobieren

Im Hauptprogramm rufst du die Funktion mergesort folgendermaßen auf:

# Ausprobieren
if __name__=="__main__":
    a=[7,6,5,4,3,2,1,0]
    print(a)
    mergesort(a, 0, len(a))
    print(a)

Hier noch ein Tipp: Wenn du ein Sortierverfahren verstehen möchtest, brauchst du Papier und Bleistift. Notiere dir die Belegung des Arrays nach jedem Schritt und führe Buch über die Werte von Indexpositionen.

Wie schnell ist Mergesort?

Du sortierst ein Array der Länge $n$ mit Mergesort, wobei $n$ eine Zweierpotenz ist.

Die Funktion merge benötigt $m$ Schritte, um zwei Teilstücke zu einem Stück der Länge $m$ zu verschmelzen. Insgesamt benötigst du also

$n$ Schritte, um $n/2$ Teilstücke der Länge 2 aus Teilstücken der Länge 1 zu verschmelzen,
$n$ Schritte, um $n/4$ Teilstücke der Länge 4 aus Teilstücken der Länge 2 zu verschmelzen,
$n$ Schritte, um $n/8$ Teilstücke der Länge 8 aus Teilstücken der Länge 4 zu verschmelzen,
und so weiter...
$n$ Schritte, um $n/n$ Teilstücke den Länge $n$ aus Teilstücken der Länge $n/2$ zu verschmelzen.

Dies sind insgesamt $n \cdot \log_2(n)$ Schritte.

Der Logarithmus zur Basis 2 von $n$ gibt die Antwort auf die Frage: "Wie oft kann ich $n$ durch 2 teilen, bis 1 herauskommt?" So kannst du beispielsweise die Zahl 8 dreimal durch 2 teilen, bis 1 herauskommt: $\log_2(8) = 3$ ).

Schneller als in $n \cdot \log_2(n)$ Schritten geht es nicht, jedenfalls wenn keine Annahmen über die Art der zu sortierenden Daten gemacht werden (zum Beispiel dass es nur Zahlen zwischen 1 und 100 sind).

Es lässt sich beweisen, dass es kein Sortierverfahren geben kann, das $n$ Daten in weniger als $n \cdot \log_2(n)$ Schritten sortieren kann.

Mergesort ist damit optimal.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?