Turingmaschine

Berechenbarkeit

Du kannst alles berechnen, was berechenbar ist!

Zwar hast du nicht die Zeit dazu, nicht die Geduld, auch nicht die Lust. Aber im Prinzip könntest du es, sogar mit Papier und Bleistift – und mit einer Anleitung, wie du vorzugehen hast. Das Einzige, was du können musst, ist Lesen und Schreiben.

Verrückt, oder? Du musst gar nicht rechnen können, sondern die Anleitung sagt dir, wie du Ziffern manipulieren musst, um Zahlen beispielsweise zu addieren.

Das alles ist tatsächlich so einfach, und deswegen kann das alles auch eine Maschine, wenn sie die richtige Anleitung hat.

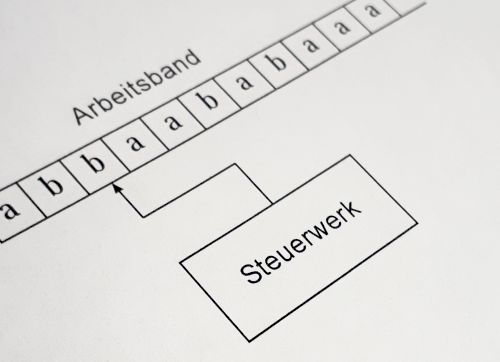
Die einfachste vorstellbare Maschine benutzt lediglich Karopapier, und sogar nur eindimensionales Karopapier, um darauf Zeichen zu lesen und zu schreiben - nach einer bestimmten Anleitung. Diese Maschine ist die Turingmaschine. Das eindimensionale Karopapier heißt Arbeitsband, und die Anleitung steckt in einer Tabelle, der sogenannten Turingtabelle. Diese Turingtabelle stellt sozusagen das Programm dar, das vom Steuerwerk der Turingmaschine ausgeführt wird.

Arbeitsweise der Turingmaschine

Die Turingmaschine kann auf den Feldern des Arbeitsbandes befindliche Zeichen lesen. Sie kann auch Zeichen neu dorthin schreiben. Und sie kann die Lese-/Schreibposition auf dem Arbeitsband nach links und nach rechts bewegen.

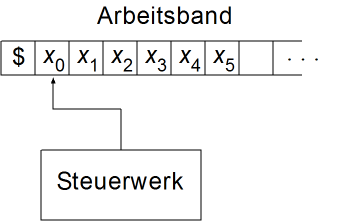
Nach links ist das Arbeitsband durch ein Bandbegrenzungszeichen $ begrenzt, nach rechts ist es unbegrenzt. Unmittelbar rechts im Anschluss an das Bandbegrenzungszeichen steht zu Beginn das Eingabewort. Alle weiteren Felder auf dem Arbeitsband enthalten Leerzeichen. Eine Schreib-/Lesemarke oder Cursor markiert jeweils die aktuelle Position auf dem Arbeitsband, an der die Turingmaschine liest oder schreibt. Zu Beginn steht der Cursor direkt rechts neben dem Bandbegrenzungszeichen.

Turingtabelle

Was die Turingmaschine genau tun soll, ist in einem entsprechenden "Programm" in Form einer Turingtabelle festgehalten. Als Beispiel siehst du hier eine sehr einfache Turingtabelle:

$\def\arraystretch{1.25} \begin{array}{llll} s & a & a' & s' \\ \hline 0 & \text a & R & 0 \\ 0 & \_ & \_ & 1^* \end{array}$

Die Turingtabelle enthält folgende Angaben:

• in der linken Spalte den momentanen Zustand $s$ der Turingmaschine,

• in der nächsten Spalte das jeweils auf dem Arbeitsband gelesene Zeichen $a$,

• in der nächsten Spalte ein Zeichen $a'$, mit dem sie das gelesene Zeichen auf dem Arbeitsband überschreibt, oder eine Cursor-Aktion L (Linksbewegung des Cursors) oder R (Rechtsbewegung des Cursors),

• in der letzten Spalte den Folgezustand $s'$, in den die Turingmaschine anschließend übergeht.

Turingtabelle ausführen

Was macht die Turingmaschine, wenn sie das "Programm" ausführt, das in der obigen Turingtabelle festgehalten ist?

Sie beginnt im Zustand 0. Auf dem Arbeitsband steht als Eingabewort eine Folge von a's und b's.

• Wenn die Turingmaschine im Zustand 0 das Zeichen a auf dem Arbeitsband liest, bewegt sie den Cursor auf dem Arbeitsband um ein Feld nach rechts (R) und bleibt im Zustand 0.

• Wenn sie im Zustand 0 dagegen ein b liest, ist kein Zustandsübergang definiert. Dann stoppt die Turingmaschine.

• Wenn sie im Zustand 0 ein Leerzeichen liest, überschreibt sie es durch ein Leerzeichen und geht in den Zustand 1 über.

Vom Zustand 1 aus ist kein Zustandsübergang mehr möglich, die Turingmaschine stoppt.

Wörter erkennen

Wenn die Turingmaschine stoppt  und sich dabei in einem Endzustand befindet, dann erkennt oder akzeptiert sie das Eingabewort. Der Zustand 1 ist in der Turingtabelle mit einem Sternchen als Endzustand gekennzeichnet. Die Turingmaschine erreicht diesen Endzustand, wenn das Eingabewort aus einer Folge von a's besteht, also keine b's enthält. Technisch gesprochen: Die Turingmaschine erkennt die Sprache $L = \{\text a^n ~|~ n \in \mathbb N_0 \}$.

Probiere einmal aus, wie diese Turingmaschine arbeitet, indem du sie auf der Webseite hwlang.de/theor/turing-simulation-an.htm simulierst.

Berechnungen ausführen

Mit einer Turingmaschine kannst du nicht nur Wörter erkennen, sondern auch Berechnungen ausführen. Das Ergebnis der Berechnung steht zum Schluss auf dem Arbeitsband, wenn die Turingmaschine stoppt und sich in einem Endzustand befindet. Hierzu findest du in den Übungsaufgaben ein Beispiel.

Formale Definition

In ähnlicher Weise wie der endliche Automat und der Stackautomat ist die Turingmaschine wie folgt formal definiert.

Das Arbeitsalphabet enthält als spezielle Zeichen das Bandbegrenzungszeichen $ und das Leerzeichen $\_$ ; diese Zeichen kommen nicht im Eingabealphabet vor.

Die Zeichen $L$ und $R$ sind die Cursor-Aktionen "gehe ein Feld nach links" und "gehe ein Feld nach rechts"; diese Zeichen kommen nicht im Arbeitsalphabet vor.

Die Übergangs­relation $d$ entspricht der oben erwähnten Turingtabelle. Die Elemente von $d$ sind 4-Tupel der Form $(s, a, a', s')$. Diese stellen mögliche Zustands­übergänge der Turing­maschine dar, mit folgender Bedeutung: Wenn die Turing­maschine im Zustand $s$ ist und das Zeichen $a$ auf dem Arbeitsband liest, so überschreibt sie es mit dem Zeichen $a'$ und geht in den Folgezustand $s'$ über. Das Zeichen $a'$ kann auch ein $L$ oder ein $R$ sein; in diesem Fall schreibt die Turing­maschine nicht, sondern bewegt den Cursor auf dem Arbeitsband nach links ($L$) oder nach rechts ($R$).

Nichtdeterministisch / deterministisch

Standardmäßig arbeitet die Turingmaschine nichtdeterministisch – es kann in der Übergangsrelation mehrere Tupel geben, die in einer bestimmten Situation anwendbar sind. Die Turingmaschine wählt dann nichtdeterministisch ein Tupel aus.

Wenn dagegen in jeder Situation immer höchstens ein Tupel der Übergangsrelation anwendbar ist, dann arbeitet die Turingmaschine deterministisch. Dies ist in dem Beispiel des vorausgehenden Abschnitts der Fall.

Eine deterministische Turingmaschine kann eine nichtdeterministische Turingmaschine simulieren – sie arbeitet einfach nacheinander alle Wahlmöglichkeiten der nichtdeterministischen Turingmaschine ab. Somit gilt:

Die Situation ist also genauso wie bei den endlichen Automaten, aber anders als bei den Stackautomaten.

Wie sich die Turingmaschine zu diesen anderen Automatentypen verhält und welche Klasse von Sprachen die Turingmaschine erkennt, erfährst du in dem Artikel über die sogenannte Chomsky-Hierarchie.