Nichts kann der Computer so gut, wie immer und immer wieder dasselbe zu tun – wie zum Beispiel in einem Iterationsverfahren. Viele Berechnungen beruhen auf Iterationen, so zum Beispiel die Berechnung von oder ( Fakultät) oder aber auch von Binomialkoeffizienten oder von Reihenentwicklungen für oder .
In einem entsprechenden Computerprogramm realisierst du eine Iteration durch eine While-Schleife. Innerhalb der While-Schleife wird eine Berechnung solange wiederholt, wie die Schleifenbedingung erfüllt ist. Aber wie entwirfst du eine While-Schleife?
Iterationsschema
Um das Ganze systematisch anzugehen, stellst du als Erstes ein Iterationsschema auf. Wenn du zum Beispiel berechnen willst, sieht das Iterationsschema folgendermaßen aus:
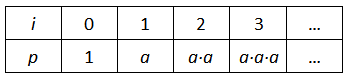
Du brauchst zwei Variablen, deren Werte sich verändern: und . Für diese legst du jeweils eine Zeile in dem Iterationsschema an. Mit der Variablen zählst du die Iterationen und mit der Variablen merkst du dir das jeweilige Zwischenergebnis . Die Werte der Variablen und verändern sich dagegen nicht.
Iterationsgleichungen aufstellen
Nun schaust du, wie jeweils der Wert einer Variablen aus dem vorher berechneten Wert hervorgeht:
Der Wert einer Variablen "mit Strich" bezeichnet dabei immer den Wert der Variablen in der vorherigen Spalte.
Du berechnest also den Wert von in jeder Spalte, indem du den Wert von aus der vorherigen Spalte nimmst und 1 hinzu addierst. Und den Wert von in jeder Spalte berechnest du, indem du den Wert von aus der vorherigen Spalte mit multiplizierst.
In der ersten Spalte, die keine vorherige Spalte hat, werden die Werte der Variablen durch Initialisierung festgelegt.
Iterationsgleichungen in ein While-Programm umsetzen
Ohne viel nachzudenken, setzt du die Iterationsgleichungen gleichsam mechanisch in ein While-Programm um. Du beginnst mit den Initialisierungen. Dann schreibst du die While-Schleife. Der Schleifenkörper besteht aus den Iterationsgleichungen.
i=0;
p=1;
while (i<n)
{
i=i+1;
p=p*a;
}Als Schleifenbedingung wählst du eine Bedingung, die im Iterationsschema für alle Spalten vor der Spalte gilt, in der du das Ergebnis der Berechnung erwartest.
Fertig! Vorausgesetzt ist, dass du alle Variablen deklariert hast und dass du die Variablen und mit Werten versehen hast.
Vorteile des Iterationsschemas
Lohnt sich der ganze Aufwand? Ja, definitiv! Auch bei dem hier gezeigten einfachsten Beispiel kannst du dich anhand des Iterationsschemas davon überzeugen, ob dein Programm korrekt ist, insbesondere
ob die Initialisierungen stimmen,
ob die Schleifenbedingung richtig ist,
ob im Schleifenkörper die richtigen Anweisungen in der richtigen Reihenfolge stehen.
Und erst recht lohnt es sich, mithilfe eines Iterationsschemas systematisch vorzugehen, wenn die Berechnung komplizierter ist. Schau dir einmal die Aufgaben an.
Sicherlich kriegst du es auch hin, die Lösungen sozusagen freihändig zu programmieren, aber mit einem Iterationsschema hast du jederzeit eine Referenz, mit der du die Korrektheit deines Programms nachvollziehen kannst.
Übungsaufgaben
Laden
Laden
