1 01. Einleitung
Warum sind Schaltnetze wichtig?
Nun ja, es ist mittlerweile recht bekannt, dass moderne Computer intern nur mit "Nullen und Einsen" arbeiten. Nur weshalb eigentlich?
Ganz einfach: Zwei Zustände lassen sich sehr leicht technisch repräsentieren, etwa als "An" und "Aus" oder elektrisch als "viel Spannung" und "wenig Spannung" (oft als "High" und "Low" bezeichnet). Bei dem Verarbeiten der Daten muss nun je nach Anforderung zwischen diesen beiden Zuständen gewechselt werden können. Das Wechseln von zwei Zuständen lässt sich sehr einfach mit einem Schalter vornehmen.
Werden zur Realisierung verschiedener Funktionen nun mehrere Schaltelemente zusammengeschlossen, also vernetzt, so spricht man von "Schaltnetzen," solange kein Speicher im Spiel ist. Dazu aber später mehr.
Fazit: Es lohnt sich auf jeden Fall, mehr über Schaltnetze zu erfahren, da diese die Basis für unsere Computer und viele elektronische Geräte bilden. Nur so können wir überhaupt ein Verständnis dafür entwickeln, wie diese Geräte technisch funktionieren.
Was kann man in diesem Kurs lernen?
Da unsere Computer nur "Nullen und Einsen" kennen, müssen alle anderen Daten erst in diese Darstellungsweise umgewandelt werden. Diesen Vorgang nennt man Codieren. Anhand von Zahlensystemen wird gezeigt, wie unsere üblichen Dezimalzahlen in Dualzahlen (0 und 1) umgewandelt werden können - und umgekehrt.
Die Verarbeitung von Daten mit den Schaltelementen unterliegt gewissen Regeln. Diese lassen sich mit der sogenannten "Schaltalgebra" beschreiben, zu der es hier eine Einführung gibt. Diese beinhaltet die wichtigsten "Funktionsbausteine", deren Verknüpfung zu Schaltnetzen, sowie verschiedene Darstellungsformen von Schaltnetzen.
Da die Funktionen ja in der Realität als Schaltkreis entwickelt werden sollen, sollten sie nur so komplex wie nötig und so einfach wie möglich sein. Mittels der Rechenregeln der Schaltalgebra kann man häufig komplexe Schaltungen vereinfachen. Dabei hilft auch eine standardisierte Darstellung der Schaltgleichungen in einer sogenannten Normalform. Wie das funktioniert, ist hier zu erfahren.
Gerade bei Aufgabenstellungen aus der Praxis entstehen im Entwurf oft sehr komplexe Schaltungen, die sich "per Hand" schwer vereinfachen lassen. In dem zugehörigen Kapitel wird gezeigt, wie man für konkrete Aufgabenstellungen eine Schaltung entwickeln kann - uns wie sich diese auf grafischem Wege vereinfachen lässt (Stichwort: KV-Diagramm).
2 02. Zahlensysteme - Dezimalzahlen & Dualzahlen
Einführung
Ich behaupte einfach mal, dass die folgenden Aussagen korrekt sind:
There are only 10 types of people in the world: Those who understand binary and those who don't.
Mit fünf Fingern kann man problemlos bis Dreißig zählen!
Stimmt doch, oder?
Tatsächlich fehlt hier eine wichtige Information um das zu beurteilen zu können: Die Aussagen stimmen für Zahlen im Dualsystem. Warum das so ist, weißt du spätestens am Ende des Artikels.
Würde man stattdessen von Dezimalzahlen ausgehen, kommt bereits bei der ersten Aussage Widerspruch. Es ist im Folgenden also immer wichtig anzugeben, in welchem Zahlensystem man sich gerade befindet.
Das Dezimalsystem hat zehn verschiedene Ziffern (0 bis 9), man sagt also, seine Basis ist 10. Das Dualsystem hat hingegen nur zwei verschiedene Ziffern (0 und 1), seine Basis ist somit die 2. Diese Basen werden auch zur Kennzeichnung verwendet und als Index an der jeweiligen Zahl vermerkt: (1 dual) und (1 dezimal).
Dezimalsystem - Basis 10
Unser alltäglich genutztes Dezimalsystem ist ein sogenanntes Stellenwertsystem. Das heißt, jede Stelle der Zahl hat eine bestimmte Wertigkeit. Man sagt daher auch: die letzte Stelle sind die Einer, die vorletzte Stelle sind die Zehner, die drittletzte Stelle sind die Hunderter … und so weiter. Wenn man die Stellen nun durchnummeriert und bei den Einern mit 0 beginnt, kann man die Wertigkeit der einzelnen Stellen sehr schön mit der Basis 10 ausdrücken ():
Einer: 1 entspricht
Zehner: 10 entspricht
Hunderter: 100 entspricht
Das gleiche Prinzip klappt auch bei den Nachkommastellen, wenn man hier vom Komma aus gesehen mit -1 beginnt:
Zehntel: 0,1 entspricht
Hundertstel: 0,01 entspricht
Wenn man als Beispiel nun die Zahl so zerlegt, ergibt sich folgende Übersicht:
Dezimalzahl: | 2 | 3 | 9 | , | 3 | 4 |
|---|---|---|---|---|---|---|
Stellennummer: | 2 | 1 | 0 | -1 | -2 | |
Stellenwert: |
|
|
|
|
| |
Potenzwert: |
| , |
Addiert man nun die einzelnen Potenzwerte der Stellen, bekommt man wieder den Gesamtwert der Zahl:
Zugegeben: Das weiß man in groben Zügen schon seit der Grundschule. Diese scheinbar umständliche Auflistung hilft jedoch gleich, das Dualsystem sehr einfach zu verstehen!
Dualsystem - Basis 2
Auch das Dualsystem ist - wie das Dezimalsystem - ein Stellenwertsystem! Daher kann man von einer gegebenen Dualzahl auf die gleiche Weise den Gesamtwert als Dezimalzahl ermitteln. Es hat jedoch nur zwei verschiedene Ziffern, also ist die Basis die 2. Als Beispiel soll hier die Zahl dienen:
Dualzahl: | 1 | 0 | 1 | , | 1 | 1 |
|---|---|---|---|---|---|---|
Stellennummer: | 2 | 1 | 0 | -1 | -2 | |
Stellenwert: | ||||||
Potenzwert: |
|
|
| , |
|
|
Addiert man nun die einzelnen Potenzwerte der Stellen, bekommt man den Gesamtwert der Dualzahl als Dezimalzahl:
Nachtrag zur Zahl 30
Die binäre Variante kann man gut mit einer Hand darstellen ;)
3 03. Zahlensysteme - Umwandlung von Dezimalzahlen in Dualzahlen
Einführung
Wie man eine Dualzahl in eine Dezimalzahl umwandeln kann, wurde bereits auf der letzten Seite gezeigt: einfach die Potenzwerte der einzelnen Stellen addieren. So erhält man beispielsweise für die Dualzahl im Dezimalsystem .
Der Weg von einer Dezimalzahl zu einer Dualzahl ist etwas aufwändiger, aber ebenfalls nicht schwer.
Variante "Scharf hinschauen"
Bei kleineren Dezimalzahlen oder ausreichendem mathematischem Vorstellungsvermögen kann man folgendes Vorgehen anwenden, für die ein "scharfes Hinschauen" nötig ist:
Schauen, welcher höchste binäre Stellenwert in die Dezimalzahl hineinpasst.
Falls ein Rest übrigbleibt, Schritt 1 wiederholen.
Alle "genutzten" Stellenwerte erhalten bei der Dualzahl eine 1, alle anderen eine 0.
Dies wird nun am Beispiel der Dezimalzahl durchgeführt:
Der größte duale Stellenwert, der in die hineinpasst, ist (entspricht 8). Also steht an der Stellennummer 3 der Dualzahl schon einmal eine 1.
Als Rest bleibt (da ). Der höchste hier hineinpassende Stellenwert ist (entspricht 4). An der Stellennummer 2 der Dualzahl steht somit auch eine 1.
Als Rest davon bleibt (da ). Der höchste hier hineinpassende Stellenwert ist (entspricht 1). An der Stellennummer 0 der Dualzahl steht ebenso eine 1.
Es verleibt kein weiterer Rest (da ). In den vorangegangenen Schritten wurden die dualen Stellenwerte mit den Stellennummern 3,2 und 0 genutzt. Diese haben bei der Dualzahl folglich die Ziffer 1, alle anderen die Ziffer 0. Also ergibt sich folgendes Ergebnis:
Variante "Systematischer Rechenweg"
Dieses Vorgehen lässt sich auch systematisieren, so dass kein scharfes Hinschauen mehr nötig ist - nur eventuell ein paar mehr Rechenschritte. Dafür ist es jedoch auch problemlos für größere Dualzahlen einsetzbar.
Ganzzahlige Dezimalzahlen
Der Weg ist folgender:
Dezimalzahl ganzzahlig durch 2 teilen und Ergebnis sowie Rest notieren
Falls das Ergebnis nicht 0 ist, Schritt 1 wiederholen (Rest darf auch 1 sein!)
Ziffern des Restes in der Reihenfolge vom letzten bis zum ersten Schritt notieren - dies ist die gesuchte Dualzahl.
Dies wird nun am Beispiel der Dezimalzahl durchgeführt:
Als Ergebnis kann man nun von unten nach oben ablesen:
Dezimalbrüche / Nachkommastellen
Bei Dezimalbrüchen wird der ganzzahlige Teil wie oben berechnet, nur für die Nachkommastellen ergeben sich leichte Abweichungen:
Nachkommastellen des Dezimalbruchs (mit gedachter 0 vor dem Komma) mit 2 multiplizieren und Ergebnis notieren.
Falls die Nachkommastellen des Ergebnisses nicht 0 sind, Schritt 1 wiederholen
Ziffern der Vorkommastellen in der Reihenfolge vom ersten bis zum letzten Schritt notieren - dies ist die gesuchte Dualzahl nach dem Komma.
Dies wird nun am Beispiel der Dezimalzahl gezeigt:
Als Ergebnis kann man nun von oben nach unten ablesen:
Kombiniert man nun die beiden letzten Beispiele, so ergibt sich folgendes:
4 04. Zahlensysteme - Übungsaufgaben
Diese Seite enthält einige Übungsaufgaben zur Umwandlung von Dezimalzahlen in Dualzahlen und umgekehrt.
Aufgabe 1
Wandle die Dualzahl in das Dezimalsystem um!
Aufgabe 2
Wandle die Dualzahl in das Dezimalsystem um!
Aufgabe 3
Wandle die Dezimalzahl in das Dualsystem um!
Aufgabe 4
Wandle die Dezimalzahl in das Dualsystem um!
Aufgabe 5
Wandle die Dezimalzahl in das Dualsystem um! Solltest du dabei auf Probleme stoßen, dann ziehe den unteren Hinweis zu Rate!
5 05. Schaltnetze - Einführung Schaltfunktionen
Zu Beginn …
Wir hatten bereits in der Einleitung des Kurses festgestellt, dass in einem Computer zur Verarbeitung der binär vorliegenden Daten Schalter eingesetzt werden - da diese sehr schön zwei Zustände abbilden können. In Form von Transistoren sind heute viele von Ihnen etwa auf einem Prozessor vertreten. In den 70er Jahren waren es ein paar Tausend Stück, die man noch gut mit der Lupe sehen konnte. In den 90er Jahren waren es bereits ein paar Millionen und heute gibt es bereits Prozessoren mit mehreren Milliarden integrierten Transistoren.
Derartige Systeme werden wir hier natürlich nicht entwickeln, sondern uns stattdessen das Grundprinzip anschauen. Wir hatten bereits festgestellt, dass es verschiedene Schaltelemente gibt, aus denen Schaltnetze zusammengesetzt werden können. Diese wollen wir uns zunächst näher ansehen.
Ganz nebenbei gilt auch hier das in der Informationstechnik so vertraute EVA-Prinzip:
Eingangswert (Eingabe) >> Schaltnetz (Verarbeitung) >> Ausgangswert (Ausgabe)
Grundfunktionen
Aus den drei Grundfunktionen lassen sich alle weiteren konstruieren! Daher bräuchte man theoretisch auch nur diese. Man kann diese Funktionen in verschiedenen Formen angeben, die äquivalent zueinander sind - wir nutzen hier die Darstellung als Gleichung, als Schaltbild und als Schaltbelegungstabelle.
Vorab noch einige Hinweise zum Verständnis:
Bei den Funktionen sind a und b jeweils Eingangswerte und y der Ausgangswert.
Die Symbole an bzw. zwischen a und b sind jeweils die Funktionssymbole für eben diese Funktion. (In Klammern ist zum Teil noch ein Alternativsymbol angegeben, welches ebenfalls üblich ist.)
Die Schaltbilder werden genutzt, um später die Schaltnetze aufzeichnen zu können. (Sie werden auch als Schaltsymbol, Logikgatter oder schlicht Gatter bezeichnet.)
In der Schaltbelegungstabelle werden alle möglichen Belegungen der Eingangswerte angegeben und dazu das Ergebnis, welches diese Funktion dabei am Ausgang liefern würde.
NOT / Nicht
in einer Gleichung:
als Schaltbild: (Hinweis: Der Kringel am Ausgang ist das eigentliche Negationssymbol!)
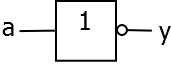
als Schaltbelegungstabelle:
a | y |
|---|---|
0 | 1 |
1 | 0 |
In Worten: Das Ergebnis ist nur 1, wenn der Eingang 0 ist.
AND / UND
in einer Gleichung:
Tipp: Das Symbol lässt sich gut merken, wenn man auf dessen Ähnlichkeit zum "A" von "AND" achtet.
als Schaltbild:
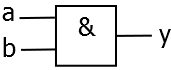
als Schaltbelegungstabelle:
a | b | y |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
In Worten: Das Ergebnis ist nur 1, wenn alle Eingänge 1 sind.
OR / ODER
in einer Gleichung:
als Schaltbild:
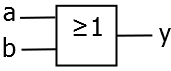
als Schaltbelegungstabelle:
a | b | y |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
In Worten: Das Ergebnis ist nur 1, wenn mindestens ein Eingang 1 ist.
Abgeleitete Funktionen
Neben den Grundfunktionen gibt es auch noch vier abgeleitete Funktionen. Diese sind nachfolgend dargestellt:
NAND
in einer Gleichung:
als Schaltbild:
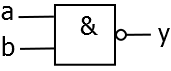
als Schaltbelegungstabelle:
a | b | y |
|---|---|---|
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
In Worten: Das Ergebnis ist nur 1, wenn nicht alle Eingänge 1 sind (Gegenteil von AND).
NOR
in einer Gleichung:
als Schaltbild:
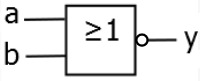
als Schaltbelegungstabelle:
a | b | y |
|---|---|---|
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
In Worten: Das Ergebnis ist nur 1, wenn alle Eingänge 0 sind (Gegenteil von OR).
XOR (Exclusiv-ODER, Antivalenz)
in einer Gleichung:
als Schaltbild:
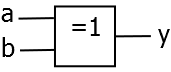
als Schaltbelegungstabelle:
a | b | y |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
In Worten: Das Ergebnis ist nur 1, wenn die Eingänge unterschiedliche Werte haben.
XNOR (Äquivalenz)
in einer Gleichung:
als Schaltbild:
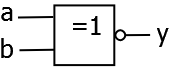
als Schaltbelegungstabelle:
a | b | y |
|---|---|---|
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
In Worten: Das Ergebnis ist nur 1, wenn die Eingänge gleiche Werte haben.
6 06. Schaltnetze - Schaltgleichung und Schaltbelegungstabelle aus Schaltbild ermitteln
Zu Beginn …
Bei der Vorstellung der Schaltfunktionen hatten wir bereits gesehen, dass diese sich jeweils als Schaltbild, als Schaltgleichung und als Schaltbelegungstabelle darstellen lassen. Anhand eines Beispiels soll nun gezeigt werden, wie man von einer gegebenen Schaltung auf eine Gleichung und auf die Schaltbelegungstabelle schließen kann.
Ermittlung der Schaltgleichung aus dem Schaltbild
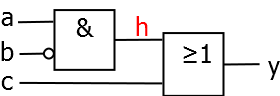
Als Beispiel haben wir das folgende einfache Schaltnetz gegeben:
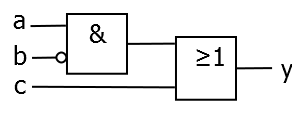
Grundsätzlich wird ein Schaltbild immer von links nach rechts und von oben nach unten gelesen. Somit sind links (oder links oben) die Eingangswerte und rechts (oder rechts unten) die Ausgangswerte.
Aus diesem Schaltbild lässt sich nun ganz einfach die Schaltgleichung ablesen:
Der Eingang von ist negiert, also liegt an diesem Eingang das Signal an
und sind miteinander UND-verknüpft:
Das Ergebnis der UND-Verküpfung wird mit ODER-verknüpft:
Das Ergebnis der ODER-Verknüpfung ist gleichzeitig das Ausgangssignal, so dass die komplette Gleichung folgendermaßen lautet:
Ermittlung der Schaltbelegungstabelle aus dem Schaltbild
Als Beispiel nutzen wir nochmal das obige Schaltnetz. In diesem markieren wir noch den Ausgang des UND-Gatters mit einer Hilfsvariable , um in der Tabelle ein Zwischenergebnis eintragen zu können - das ist später hilfreich, um die Übersicht zu behalten.
Schritt 1 - Tabellenkopf erstellen
Zuerst erstellen wir die leere Tabelle. Um sie übersichtlich zu gestalten brauchen wir insgesamt 6 Spalten:
für die drei Eingangssignale (),
für das negierte Eingangssignal ,
für die Hilfsvariable als Zwischenergebnis von der UND-Verküpfung
und schließlich für das Ausgangssignal y
…
Schritt 2 - Eingangswerte eintragen
Als zweites tragen wir für die Eingangssignale nun alle möglichen Kombinationen ein, die auftreten können. Hierbei ist für uns folgende Feststellung wichtig: ==Bei Eingangswerten gibt es genau verschiedene Möglichkeiten!== In unserem Fall sind das Möglichkeiten und damit 8 Zeilen in der Tabelle.
Füllt man diese Werte systematisch aus, minimieren sich auch die Fehler dabei:
Bei dem ersten Eingangssignal die erste Hälfte der Zeilen mit einer 0, die zweite Hälfte mit einer 1 füllen.
Bei dem nächsten Eingangssignal halb so viele Zeilen nacheinander mit einer 0 und dann mit einer 1 füllen (und dies wiederholen, bis alle Zeilen gefüllt sind)
Schritt 2 für alle weiteren Eingangswerte wiederholen (und dabei Anzahl der Zeilen für Wechsel zwischen 0 und 1 immer weiter halbieren)
Wir tragen dann auch gleich noch die Werte von mit ein, wobei ja nur die Nullen und Einsen aus der Spalte von "vertauscht" werden. Das sieht dann folgendermaßen aus:
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
0
Schritt 3 - Zwischenergebnisse eintragen
Wir haben in unserem Fall nur ein Zwischenergebnis - und zwar das Ergbenis der UND-Verknüpfung als Hilfsvariable . Wie war doch gleich das Ergebnis einer UND-Verknüpfung festgelegt? Also welche Werte müssen und haben, damit ist?
Richtig ;) Die Hilfsvariable ist genau dann 1, wenn sowohl als auch den Wert 1 haben! Das ist an genau zwei Stellen der Fall. Und so tragen wir in diesen Zeilen für eine 1 ein, in allen anderen Zeilen jedoch eine 0.
0
0
0
1
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
1
0
0
1
1
1
0
1
1
1
1
1
0
0
0
1
1
1
0
0
Schritt 4 - Ausgangswerte eintragen
Als letzten Schritt müssen wir jetzt noch die Ausgangswerte eintragen. Hierbei hilft es uns nun, dass wir ein Zwischenergebnis aufgestellt haben, denn so lassen sich die Ausgangswerte als Ergebnis der OR-Verknüpfung leicht ermitteln:
Wie war doch gleich das Ergebnis einer OR-Verknüpfung festgelegt? Also welche Werte müssen und haben, damit ist?
Richtig ;) Das Ausgangssignal ist genau dann 1, wenn mindestens ein Wert von oder den Wert 1 hat! Das ist an genau fünf Stellen der Fall. Und so tragen wir in diesen Zeilen für eine 1 ein, in allen anderen Zeilen jedoch eine 0.
0
0
0
1
0
0
0
0
1
1
0
1
0
1
0
0
0
0
0
1
1
0
0
1
1
0
0
1
1
1
1
0
1
1
1
1
1
1
0
0
0
0
1
1
1
0
0
1
Damit sind wir fertig :)
7 07. Schaltgleichung aus Schaltbelegungstabelle ermitteln
Zu Beginn …
Wir haben bereits gelernt, wie man aus einem Schaltbild die Schaltgleichung ablesen und die Schaltbelegungstabelle ermitteln kann.
In der Realität ist aber oft für eine konkrete Aufgabenstellung nur bekannt, welche Eingangs- und welche zugehörigen Ausgangswerte es geben soll. Diese werden in eine Schaltbelegungstabelle eingetragen. Nun muss anhand dieser Tabelle die Schaltgleichung (und anschließend die Schaltung) entwickelt werden. Wie das geht? Das schauen wir uns gleich an!
Ablesen der Normalformen
Man könnte nun einfach alle Informationen aller Zeilen einer Schaltbelegungstabelle in die Schaltgleichung aufnehmen. Dadurch würde eine sehr umfangreiche Gleichung entstehen.
Es hat sich aber gezeigt, dass dies gar nicht nötig ist. Denn es reicht entweder aufzunehmen, wie der Ausgangswert 1 zustande kommen kann (alles andere würde ja zum Ausgangswert 0 führen); oder man nimmt nur die "Eingangswert-Kombinationen" auf, die zum Ausgangswert 0 führen (alles andere würde ja zum Ausgangswert 1 führen).
Um genau dies fehlerfrei erledigen zu können, haben sich die sogenannten Normalformen etabliert:
DNF (Disjunktive Normalform)
In den Zeilen mit dem Ausgangswert 1 jeweils alle Eingangssignale UND-verknüpfen (den in jeder Zeile entstehenden Ausdruck nennt man "Min-Term")
Alle Min-Terme ODER-verknüpfen
KNF (Konjunktive Normalform)
In den Zeilen mit dem Ausgangswert 0 jeweils alle Eingangssignale ODER-verknüpfen (den in jeder Zeile entstehenden Ausdruck nennt man "Max-Term")
Alle Max-Terme UND-verknüpfen
Es bietet sich also an, bei vielen 1er-Ausgangswerten eine DNF zu erzeugen und bei vielen 0er-Ausgangswerten eine KNF zu erzeugen, um die entstehende Gleichung möglichst kurz zu halten.
Beispiel:
Nehmen wir als Beispiel die Schaltbelegungstabelle der XOR-Funktion:
a
b
y
0
0
0
0
1
1
1
0
1
1
1
0
Bei dieser ist es egal, ob wir eine DNF oder eine KNF erzeugen, da es bei den Ausgangswerten gleichviele Einsen und Nullen gibt. Nach der eben genannten Anleitung abgelesen, ergeben sich folgende Gleichungen:
Disjunktive Normalform:
Min-Term der Zeile 2:
Min-Term der Zeile 3:
ODER-Verknüpfung der Min-Terme:
Gesamte Gleichung
Konjunktive Normalform:
Max-Term der Zeile 1:
Max-Term der Zeile 4:
UND-Verknüpfung der Max-Terme:
Gesamte Gleichung
Damit sind wir fertig :) Gleichzeitig haben wir so zwei Varianten gefunden, wie man nur mit den drei Grundfunktionen NOT, AND und OR die abgeleitete XOR-Funktion konstruieren kann.
Übung:
Ermittle für die folgende Schaltbelegungstabelle eine Schaltgleichung! Wähle dafür eine günstige Normalform aus!
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
Nachtrag
Falls du sehr aufmerksam gewesen bist, kam dir die Schaltbelegungstabelle der Übung vielleicht bekannt vor!? Es war nämlich die von der letzten Seite zum Thema "Schaltbelegungstabelle aus dem Schaltbild ermitteln", nur, dass die Spalten mit den Hilfsgrößen fehlten. Und wenn du dich genau zurückerinnern kannst, war dort die Schaltgleichung irgendwie kürzer … nämlich so:
Wie kann das sein?
Tatsächlich kann es für denselben Sachverhalt viele verschiedene Schaltgleichungen geben, die das gleiche Ergebnis liefern. Manche sind jedoch kürzer bzw. einfacher und damit effizienter als andere, gerade wenn es um die Umsetzung als Schaltung geht!
Also sollte unser Ziel sein, möglichst minimale Schaltgleichungen zu entwickeln. Wie das geht, ist auf den folgenden Seiten zu erfahren!
8 08. Schaltgleichungen rechnerisch vereinfachen mittels Schaltalgebra
Zu Beginn …
Wir haben auf der letzten Seite festgestellt, dass Schaltgleichungen recht lang sein können - und dass es für eine lange Gleichung möglicherweise eine kürzere Variante gibt, welche genau dasselbe Ergebnis liefert.
Doch wie können wir Schaltgleichungen sicher vereinfachen?
Regeln der Schaltalgebra
Die Schaltalgebra gibt uns Möglichkeiten an die Hand, wie wir mit Schaltgleichungen rechnen, sie umformen und vereinfachen können.
Ein schönes Beispiel für die Vereinfachung ist hier die Gleichung :
Diese besagt, dass der Ausgangswert auf jeden Fall von abhängt - und auch von oder . Kurzum: Es ist eigentlich egal, welchen Wert hat. Also kann man die Angabe auch gleich weglassen und stattdessen schreiben: .
Eine ganze Liste derartiger Regeln findet sich in folgender Tabelle. Schau sie dir einfach mal in Ruhe durch und versuche, sie grob nachzuvollziehen!
Nr. | Regel | Kommentar |
|---|---|---|
1 |
| Konjunktion mit Variable |
2 |
| '' |
3 |
| '' |
4 |
| '' |
5 |
| Disjunktion mit Variable |
6 |
| '' |
7 |
| '' |
8 |
| '' |
9 |
| Doppelte Negation |
10 |
| '' |
11 |
| '' |
12 |
| Kommutativgesetze (Vertauschung) |
13 |
| '' |
14 |
| Assoziativgesetze (Zusammenfassung) |
15 |
| '' |
16 |
| Distributivgesetze |
17 |
| '' |
18 |
| Gesetze von de Morgan |
19 |
| '' |
20 |
| Kürzungsregeln |
21 |
| '' |
22 |
| '' |
23 | '' | |
24 | '' | |
25 |
| '' |
Beispiel zur Anwendung der Rechenregeln
Nehmen wir an dieser Stelle noch einmal das obige Einführungsbeispiel, um den Umgang mit den Rechenregeln zu verdeutlichen:
Ausgangsgleichung:
Vorgehensweise:
Für den Ausdruck in der Klammer gilt laut Regel 8:
Führen wir nun die UND-Verknüpfung von mit dem Ergebnis des Klammerausdrucks durch, so erhalten wir nach Regel 2:
Somit erhalten wir als vereinfachte Gleichung:
Hinweis:
Dies ist im Übrigen nicht der einzige Weg. Mit der Anwendung der Regeln 16 und 24 würde man beispielsweise auch auf dieses Ergebnis kommen! Probier' es einfach mal aus!
Bei der Arbeit mit den Regeln der Schaltalgebra heißt es also: Regeln verinnerlichen und ganz genau hinschauen ;)
9 09. Schaltnetze - Übungen zum Entwickeln und Vereinfachen
Aufgabe 1
Vereinfache die folgende Schaltgleichung:
Aufgabe 2
Vereinfache die folgende Schaltgleichung:
Aufgabe 3
Ermittle für die angegebene Schaltung die zugehörige Schaltgleichung. Vereinfache diese anschließend weitestmöglich.
Zusatz: Versuche die vereinfachte Schaltgleichung so umzuformen, dass nur eine Sorte Logikgatter nötig ist.
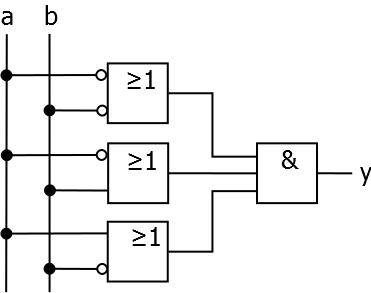
Aufgabe 4
Ermittle aus der angegebenen Schaltbelegungstabelle eine Schaltgleichung. Wähle dafür eine sinnvolle Normalform.
Vereinfache diese Schaltgleichung rechnerisch mithilfe der Schaltalgebra.
Gib zu der vereinfachten Schaltgleichung eine Schaltung an.
a | b | c | y |
|---|---|---|---|
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
10 10. Schaltgleichungen grafisch vereinfachen mittels KV-Diagramm
Zu Beginn …
Vielleicht ist dir bei den Übungen zum rechnerischen Vereinfachen von Schaltgleichungen aufgefallen, dass dieses Vorgehen doch so seine Tücken hat. Wenn man hierin keine große Übung hat oder die Gleichungen komplizierter werden, dann übersieht man oftmals Vereinfachungsmöglichkeiten.
Daher wurde für die manuelle Vereinfachung von Schaltgleichungen auch ein grafisches Verfahren entwickelt, die sogenannten KV-Diagramme. Sie sind benannt nach Ihren Entwicklern Maurice Karnaugh und Edward Veitch. Sie dienen dazu, eine Schaltbelegungstabelle so aufzuschreiben, dass man mit wenig Mühe daraus direkt die vereinfachte Schaltgleichung in einer der Normalformen ablesen kann.
Die das funktioniert? Das lernst du auf dieser Seite!
Beispiel "Dualzahlen-Vergleicher"
Wir schauen uns nun ein ganz konkretes Beispiel an, bei dem wir aus einer Aufgabenstellung heraus zunächst die Schaltbelegungstabelle aufstellen. Diese wandeln wir dann in ein KV-Diagramm um und lesen daraus direkt eine vereinfachte Schaltgleichung in Normalform ab.
Aufgabenstellung
Ermittle eine möglichst minimale Schaltgleichung für ein Schaltnetz, welches zwei zweistellige Dualzahlen ( und ) miteinander vergleichen kann. Das Ergebnis soll sein, wenn . Es soll dagegen sein, wenn .
Schritt 1: Schaltbelegungstabelle aufstellen
Wir haben als Eingangswerte zwei zweistellige Dualzahlen und somit insgesamt vier Dualziffern, die sich ändern können. Wie viele Zeilen braucht also unsere Tabelle?
Richtig ;)
Für die Kombination der vier Dualziffern gibt es verschiedene Möglichkeiten. Somit braucht unsere Schaltbelegungstabelle auch 16 Zeilen. In diese können wir gleich die Eingangswerte eintragen:
0 | 0 | 0 | 0 | |
0 | 0 | 0 | 1 | |
0 | 0 | 1 | 0 | |
0 | 0 | 1 | 1 | |
0 | 1 | 0 | 0 | |
0 | 1 | 0 | 1 | |
0 | 1 | 1 | 0 | |
0 | 1 | 1 | 1 | |
1 | 0 | 0 | 0 | |
1 | 0 | 0 | 1 | |
1 | 0 | 1 | 0 | |
1 | 0 | 1 | 1 | |
1 | 1 | 0 | 0 | |
1 | 1 | 0 | 1 | |
1 | 1 | 1 | 0 | |
1 | 1 | 1 | 1 |
Wenn man jetzt mit einer so langen Tabelle hantiert, so bietet es sich der Übersicht halber an, die Zeilen zu nummerieren. Bei einem Blick auf die Eingangswerte in der Tabelle fällt auf, dass diese zeilenweise die Dezimalzahlen 0 bis 15 als Dualzahlen beinhalten (0000 bis 1111). So kann man dies gleich für die Nummerierung ausnutzen:
Nr. |
|
|
|
|
|
|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 0 | |
1 | 0 | 0 | 0 | 1 | |
2 | 0 | 0 | 1 | 0 | |
3 | 0 | 0 | 1 | 1 | |
4 | 0 | 1 | 0 | 0 | |
5 | 0 | 1 | 0 | 1 | |
6 | 0 | 1 | 1 | 0 | |
7 | 0 | 1 | 1 | 1 | |
8 | 1 | 0 | 0 | 0 | |
9 | 1 | 0 | 0 | 1 | |
10 | 1 | 0 | 1 | 0 | |
11 | 1 | 0 | 1 | 1 | |
12 | 1 | 1 | 0 | 0 | |
13 | 1 | 1 | 0 | 1 | |
14 | 1 | 1 | 1 | 0 | |
15 | 1 | 1 | 1 | 1 |
Jetzt müssen wir noch die Ausgangswerte eintragen: Diese sollen sein, wenn (und , wenn ). Fülle diese Spalte zur Übung am Besten selbst einmal aus, bevor zu weiterliest!
So, die vollständige Schaltbelegungstabelle sieht folgendermaßen aus:
Nr. |
|
|
|
|
|
|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 1 | 1 |
2 | 0 | 0 | 1 | 0 | 1 |
3 | 0 | 0 | 1 | 1 | 1 |
4 | 0 | 1 | 0 | 0 | 0 |
5 | 0 | 1 | 0 | 1 | 0 |
6 | 0 | 1 | 1 | 0 | 1 |
7 | 0 | 1 | 1 | 1 | 1 |
8 | 1 | 0 | 0 | 0 | 0 |
9 | 1 | 0 | 0 | 1 | 0 |
10 | 1 | 0 | 1 | 0 | 0 |
11 | 1 | 0 | 1 | 1 | 1 |
12 | 1 | 1 | 0 | 0 | 0 |
13 | 1 | 1 | 0 | 1 | 0 |
14 | 1 | 1 | 1 | 0 | 0 |
15 | 1 | 1 | 1 | 1 | 0 |
Zwischenfazit:
In der Spalte der Ausgangswerte stehen sechs Einsen und 10 Nullen. Würden wir jetzt einfach die Normalformen aus der Tabelle ablesen, so hätte die DNF sechs Klammerausdrücke (Min-Terme) und die KNF sogar 10 Klammerausdrücke (Max-Terme) mit je 4 Schaltvariablen. Diese Schaltgleichungen "per Hand" rechnerisch zu vereinfachen wäre schon recht aufwändig …
Schritt 2: KV-Diagramm aufstellen
Daher nutzt man für die manuelle Vereinfachung lieber die grafische Variante mittels KV-Diagramm (auch Karnaugh-Tafel genannt). Diese beruht auf den Regeln der Schaltalgebra und hier vor allem darauf, dass eine Schaltvariable in einem Term oft entfallen kann, wenn sie sowohl negiert als auch nichtnegiert darin auftritt.
a) Matrix aufzeichnen und beschriften
Zunächst müssen wir eine sogenannte Matrix aufstellen - quasi eine "Spezial- Tabelle". Da wir in unserer Schaltbelegungstabelle 16 Zeilen haben, hat die Matrix 16 Felder. Wir brauchen somit eine 4x4-Matrix.
An der linken und der oberen Seite wird die Beschriftung angefügt. In unserem Fall erscheinen links die beiden Eingangswerte der Dualzahl und oben die beiden Eingangswerte der Dualzahl . Für beide Dualzahlen gibt es ja vier verschiedene Möglichkeiten: , , und .
Man könnte nun einfach die vier Zeilen und Spalten der Matrix in dieser Reihenfolge damit beschriften. Allerdings bekommt man dann kein KV-Diagramm ;)
Bei einem KV-Diagramm müssen die Felder nämlich so angeordnet werden, dass nachher die Schaltvariablen möglichst negiert als auch nichtnegiert nebeneinander stehen - nur dann lassen sie sich nämlich herauskürzen. Das gelingt genau dann, wenn sich die Beschriftungen der Zeilen bzw. Spalten nacheinander nur in jeweils 1 Bit unterscheiden.
Konkret heißt das:
Bei der ersten Zeile und Spalte sind die Eingangswerte jeweils .
Bei der zweiten Zeile und Spalte darf nun nur eine der Nullen zu einer Eins werden. Also erhalten sie die Beschriftung . (Das hätte man wohl auch intuitiv als zweites genommen.)
Bei der dritten Zeile und Spalte müssen wir allerdings aufpassen: statt dual weiter zu zählen (und eine zu vergeben), werden diese mit beschriftet !!!
Die vierte Zeile und Spalte erhalten schließlich die Beschriftung .
Das Ganze sieht dann folgendermaßen aus:
b) Matrix-Felder nummerieren
Wenn man sich nun einmal die erste Zeile der Matrix anschaut, so erkennt man schnell deren "Abstammung" von der Schaltbelegungstabelle: Das erste Feld der Matrix entspricht der ersten Zeile der Schaltbelegungstabelle (Zeile Nr. 0, alle Eingangswerte sind ).
Das zweite Feld entspricht der zweiten Zeile (Zeile Nr.1, nur der Eingangswert ist ). Das dritte Feld der Matrix entspricht durch die "besondere Anordnung" allerdings der vierten Zeile der Tabelle - und das vierte Feld der dritten Zeile.
Um den Überblick zu behalten, lohnt es sich daher, die Felder passend zu den Tabellenzeilen zu nummerieren:
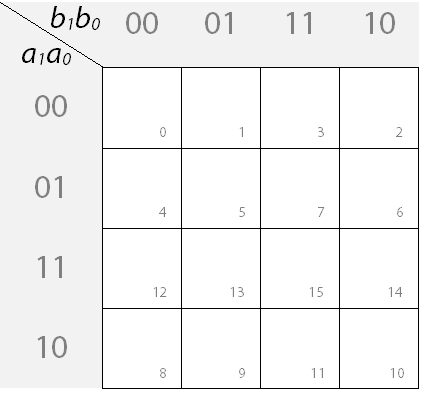
Zwischenfazit:
Ganz schön viel Aufwand, oder? Und das soll schneller und fehlerfreier gehen als die rechnerische Variante? Ja! Denn für eine häufig auftretende Schaltbelegungstabelle mit 16 Zeilen sieht das Grundgerüst eines KV-Diagramms immer so aus - nur die Variablen heißen anders. Aber die sonstige Beschriftung und Nummerierung ändert sich nicht. Hat man sich das Prinzip einmal eingeprägt, geht das Aufschreiben fix von der Hand! Aber sehen wir weiter …
c) Ausgangswerte aus Schaltbelegungstabelle eintragen
Dieser Schritt ist nun wirklich simpel: Einfach die Ausgangswerte aus der jeweiligen Zeile der Schaltbelegungstabelle in das entsprechende Feld des KV-Diagramms übertragen. Dabei erhältst du folgendes Ergebnis:
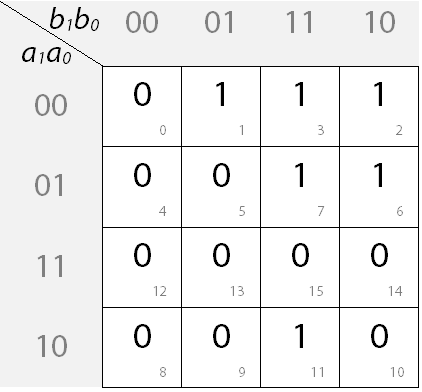
d) Blockbildung von Werten im KV-Diagramm
Jetzt kommt endlich die grafische Komponente ins Spiel. Es lohnt sich also, ein paar verschiedenfarbige Stifte zur Hand zu haben.
An dieser Stelle bildet man nun rechteckige Blöcke von Einsen (für eine DNF) oder Nullen (für eine KNF). Wir wählen hier effizienter Weise die Blockbildung von Einsen, da es weniger von ihnen gibt.
Die Blöcke müssen jeweils eine Anzahl von Einsen beinhalten, die einer Zweierpotenz entspricht (1, 2, 4, 8, usw.). Diese sollen möglichst groß sein und sie dürfen sich auch überlappen. Die Blöcke können auch über den Rand hinaus gehen - sie setzen dann an der gegenüberliegenden Seite fort. Am Ende sollen alle Einsen einem Block angehören.
Bei unserem Beispiel können wir rechts oben einen Viererblock bilden (Felder 2,3,6,7), einen "normalen" Zweierblock (Felder 1 und 3), sowie einen Zweierblock "über den Rand hinaus" (Felder 3 und 11). In das Diagramm eingetragen ergibt sich folgendes Bild:
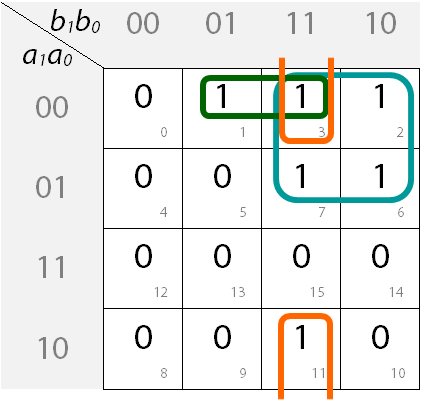
Schritt 3: Schaltgleichung ablesen
Nun können wir mithilfe der Blöcke direkt die minimierte Schaltgleichung in disjunktiver Normalform ablesen.
Innerhalb der Blöcke können dabei alle Schaltvariablen entfallen, die sowohl negiert, als auch nicht negiert auftauchen.
Schauen wir uns dazu den Viererblock an (türkis; Felder 2, 3, 6, 7):
In diesem ist einmal mit dem Eingangswert (3. Spalte) und einmal mit dem Eingangswert (4. Spalte) vertreten - also einmal nichtnegiert und einmal negiert. Daher entfällt bei der anschließenden Min-Term-Bildung dieses Blocks.
Dasselbe gilt für die Schaltvariable . Diese ist in der 1. Zeile mit Eingangswert vorhanden und in der 2. Zeile mit Eingangswert ). Daher entfällt auch sie bei der Min-Term-Bildung dieses Blocks.
Übrig bleiben also nur noch die Schaltvariable (Eingangswert in den Zeilen 1 und 2), sowie die Schaltvariable (Eingangswert in den Spalten 3 und 4).
Der Min-Term des Viererblocks lautet also:
"Normaler" Zweierblock (grün; Felder 1 und 3):
In diesem ist mit unterschiedlichen Eingangswerten enthalten (2. und 3. Spalte) und kann deshalb bei der anschließenden Min-Term-Bildung dieses Blocks entfallen. Alle anderen Schaltvariablen werden einbezogen.
Der Min-Term des "normalen" Zweierblocks lautet somit:
Zweierblock "über den Rand hinaus" (orange; Felder 3 und 11):
In diesem ist mit unterschiedlichen Eingangswerten enthalten (1. und 4. Zeile) und kann deshalb bei der anschließenden Min-Term-Bildung dieses Blocks entfallen. Alle anderen Schaltvariablen werden einbezogen.
Der Min-Term dieses Zweierblocks lautet somit:
Die komplette Schaltgleichung lautet somit:
Lösung im Überblick
Ausgefülltes KV-Diagramm:

minimierte Schaltgleichung in disjunktiver Normalform:
Das Vereinfachen war doch tatsächlich einfach, nicht wahr ;)
11 11. Komplexaufgabe zu Schaltnetzen - 7-Segment-Anzeige
Aufgabenstellung
Entwickle möglichst einfache Schaltgleichungen in disjunktiver Normalform für die sieben Segmente einer 7-Segmentanzeige, um mit dieser die Dezimalziffern 0-9 darstellen zu können. Dabei soll die nachfolgend angegebene Darstellung der Dezimalziffern auf der 7-Segmentanzeige erreicht werden. Zeichne die Schaltung für das Segment .

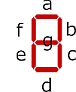
Hinweise:
Die Dezimalziffern liegen eingangsseitig binär codiert als Dualzahlen vor. Diese haben eine Wortbreite von 4 Bit (das heißt, sie haben 4 Binärstellen und ggf. führende Nullen, so z.B. ).
Nutze für die Stellen der Dualzahlen die Bezeichnungen bis .
Für die Segmente sollen die in der Grafik gegebenen Bezeichnungen bis genutzt werden.
Eine "1" am Eingang des jeweiligen Segments soll bedeuten, dass es leuchtet und eine "0", dass es nicht leuchtet.
Zeilen in der Schaltbelegungstabelle, die für unsere Schaltung nicht relevant sind (don't care), erhalten einfach Sterne als Ausgangswerte. Diese können dann bei der Blockbildung in KV-Diagrammen wahlweise als "1" oder "0" aufgefasst werden.
