Flächen kannst du in verschiedene Einheiten umrechnen. Wie das geht, erfährst du in diesem Artikel.
Übersicht Flächeneinheiten
Bezeichnung | Einheitszeichen | Bezug zur nächstkleineren Größe |
|---|---|---|
Quadratkilometer | ||
Hektar | ||
Ar | ||
Quadratmeter | ||
Quadratdezimeter | ||
Quadratzentimeter | ||
Quadratmillimeter |
Umrechnungen
zum Vergleich: Längeneinheiten | Flächeneinheiten | zum Vergleich: Volumeneinheiten |
|---|---|---|
Erklärung und Beispiele
In diesem Video wird eine Übersicht zu der Umrechnung von Flächeneinheiten erklärt. Außerdem werden in diesem Video Beispielaufgaben mit Hilfe der Übersicht gelöst.
Laden
Einheitentafel
Besonders gut geht das Umrechnen mit der Einheitentafel:
Dazu legt man, von rechts beginnend, jeweils 2 Spalten für , usw. an.
Wichtig ist also, dass man bei den Flächeneinheiten jeweils 2 Spalten reserviert, wo bei den Längeneinheiten nur 1 Spalte ist und bei den Volumeneinheiten 3 Spalten sind.
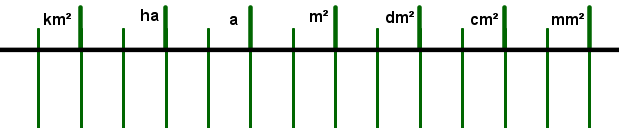
Zum Umrechnen einer Flächenangabe trägt man die angegebene Größe bei der betreffenden Einheit ein, und zwar so, dass die Einerziffer bzw. das Komma der Zahl gerade dort steht, wo die angegebene Einheit beginnt / endet.
Freibleibende Plätze können mit Nullen aufgefüllt werden.
Beispiel:
Eingetragen werden sollen

Aus der so ausgefüllten Einheitentafel kann man nun leicht die umgerechnete Flächenangabe ablesen.
Beispiel:
Aus obiger Einheitentafel kann man beispielsweise entnehmen:
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Umrechnen von Flächeneinheiten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
