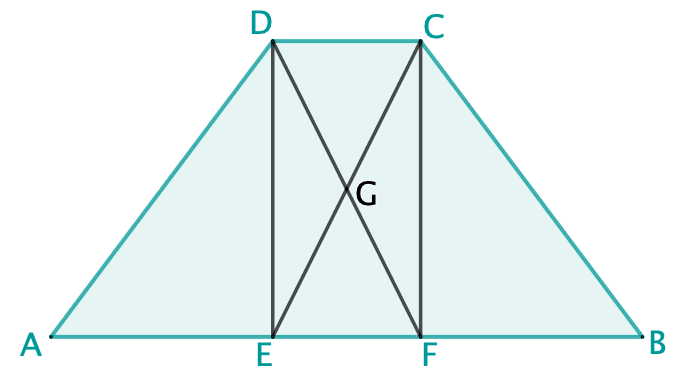
Das Viereck ABCD ist ein achsensymmetrisches Trapez. Bestimme alle zueinander kongruente Teildreiecke im Trapez und begründe deine Antwort.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Das Viereck ABCD ist ein achsensymmetrisches Trapez. Bestimme alle zueinander kongruente Teildreiecke im Trapez und begründe deine Antwort.
