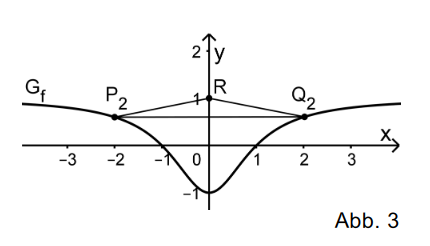
Teilaufgabe a)

$k=2$. $f\left(x\right)=\frac{x^2-1}{x^2+1}\ \ \Rightarrow\ f\left(2\right)=\frac{2^2-1}{2^2+1}=\frac{3}{5}$

Damit $P_2\left(-2;\frac{3}{5}\right)\ \ Q_2\left(2;\frac{3}{5}\right)$$R\left(0;1\right)$

Die Grundseite g des Dreiecks ist die Strecke $P_2Q_2$.

Somit gilt für die Grundseite $g=4.$

Die Höhe h ist die Strecke zwischen dem Punkt R und der y-Koordinate von $P_2$.

Somit gilt für die Höhe $h=1-\frac{3}{5}=\frac{2}{5}.$

Also berechnet sich der Flächeninhalt des Dreiecks $RP_2Q_2$ zu: $A\left(2\right)=\frac{1}{2}\cdot4\cdot\frac{2}{5}=\frac{4}{5}FE$.

Im allgemeinen Fall gilt für die Grundseite $g=2\cdot k$ und für die Höhe $h=1-f\left(k\right)=1-\frac{k^2-1}{k^2+1}=\frac{\left(k^2+1-\left[k^2-1\right]\right)}{k^2+1}$

Also $h=\frac{k^2+1-k^2+1}{k^2+1}=\frac{2}{k^2+1}$.

Für den Flächeninhalt gilt dann:

$A\left(k\right)_{ }=\frac{1}{2}\cdot2\cdot k\cdot\frac{2}{k^2+1}=\frac{2k}{k^2+1}$.

Teilaufgabe b)

Zeige, dass es ein $k>0$ gibt, so dass $A\left(k\right)$ maximal wird.

Mit Hilfe der 1.Ableitung von $A\left(k\right)$ sucht man eine Maximumstelle.

$A'\left(k\right)=2\cdot\frac{\left(1\cdot\left(k^2+1\right)-k\cdot2\cdot k\right)}{\left(k^2+1\right)^2}=2\cdot\frac{\left(k^2+1-2k^2\right)}{\left(k^2+1\right)^2}$

$A'\left(k\right)=2\cdot\frac{\left(1-k^2\right)}{\left(k^2+1\right)^2}$.

$A'\left(k\right)=0\Leftrightarrow\ 1-k^2=0\Leftrightarrow\text{k}^2=1\Leftrightarrow\text{k}=1$, da $k>0$. Das Vorzeichen von $A'\left(k\right)$ wird nur vom Zähler $z=1-k^2$ bestimmt. Denn der Nenner ist als Quadrat nicht negativ.

Graphisch dargestellt ist $z$ eine nach unten geöffnete Normalparabel um 1 nach oben verschoben.

Somit ändert $A'\left(k\right)$ an der Stelle $k=1$ das Vorzeichen von plus zu minus. Also ist $k=1$ Maximumstelle.

Damit ergibt sich für den maximalen Flächeninhalt:

$A_{\max}=2\cdot\frac{1}{\left(1^2+1\right)}=\frac{2}{2}=1FE.$