Analysis, Teil B, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die in $ℝ$ definierte Funktion $f : x \mapsto \frac{x^{2} - 1}{x^{2} + 1}$ ; die Abbildung 1 zeigt ihren Graphen $G_{f}$ .
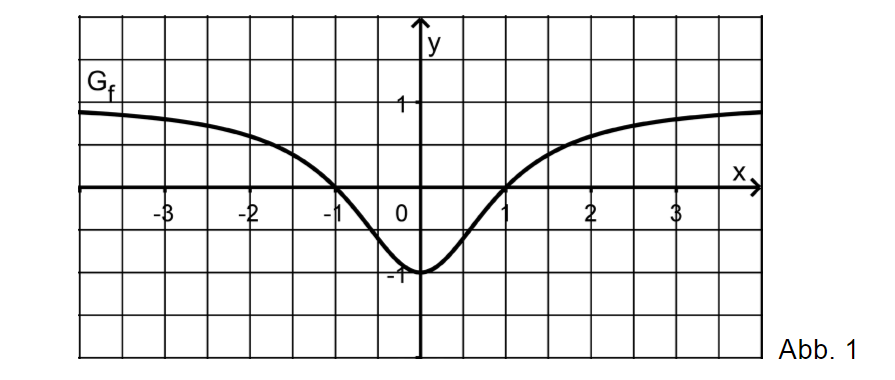
a) Bestätigen Sie rechnerisch, dass $G_{f}$ symmetrisch bezüglich der $y$ -Achse ist, und untersuchen Sie anhand des Funktionsterms das Verhalten von $f$ für $x \to + \infty$ Bestimmen Sie diejenigen $x$ -Werte, für die $f (x) = 0,96$ gilt.
b) Untersuchen Sie rechnerisch das Monotonieverhalten von $G_{f}$ .
(zur Kontrolle: $f ‘ (x) = \frac{4 x}{(x^{2} + 1)^{2}}$ )
c) Bestimmen Sie rechnerisch eine Gleichung der Tangente $t$ an Punkt $G_{f}$ im Punkt $(3 | f (3)$ . Berechnen Sie die Größe des Winkels, unter dem $t$ die $x$ -Achse schneidet, und zeichnen Sie $t$ in die Abbildung 1 ein.

Teilaufgabe a)
Die vorgelegte Funktion ist eine gebrochen rationale Funktion, wobei Zählergrad gleich dem Nennergrad. Da der Nenner eine Summe nicht negativer Summanden ist und insgesamt immer positiv ist, ist die Funktion für alle reellen Zahlen definiert.
Zum Nachweis der Achsensymmetrie:
$f (x) = f (- x)$ , für alle x
$f (x) = \frac{x^{2} - 1}{x^{2} + 1}$
$f (- x) = \frac{{(- x)}^{2} - 1}{{(- x)}^{2} + 1} = \frac{(x^{2} - 1)}{x^{2} + 1}$ $= f (x)$ . Achsensymmetrisch.
Zum Verhalten im Unendlichen:
Man kürzt den Quotienten mit $x^{2}$
$f (x) = \frac{\frac{x^{2}}{x^{2}} - \frac{1}{x^{2}}}{\frac{x^{2}}{x^{2}} + \frac{1}{x^{2}}} = \frac{1 - \frac{1}{x^{2}}}{1 + \frac{1}{x^{2}}} \to 1$
$f (x) = 0,96 \Leftrightarrow \frac{(x^{2} - 1)}{x^{2} + 1} = 0,96 \Leftrightarrow$
$0,96 \cdot x^{2} + 0,96 = x^{2} - 1 \Leftrightarrow - 0,04 \cdot x^{2} = - 1,96 \Leftrightarrow$
$x^{2} = 49 \Leftrightarrow x = - 7 oder x = 7.$
Teilaufgabe b)
Zum Monotonieverhalten benutzt man die erste Ableitung. f ist eine gebrochen rationale Funktion, also kommt die Quotientenregel zur Anwendung.
$f^{'} (x) = \frac{2 x \cdot (x^{2} + 1) - (x^{2} - 1) \cdot 2 x}{{(x^{2} + 1)}^{2}} = \frac{2 x \cdot (x^{2} + 1 - x^{2} + 1)}{{(x^{2} + 1)}^{2}}$
$f^{'} (x) = 4 \cdot \frac{x}{{(x^{2} + 1)}^{2}}$ .
Das Vorzeichen von $f^{'}$ wird nur vom Zähler bestimmt, da der Nenner als Quadrat keinen Vorzeichenwechsel hat.
Der Zähler $x$ wird graphisch durch die 1. Winkelhalbierende dargestellt. Also ergibt sich:
$f^{'} (x) < 0, f a l l s x < 0 \Rightarrow f s t r e n g m o n o t o n f a l l e n d$ .
$f^{'} (x) > 0, f a l l s x > 0 \Rightarrow f s t r e n g m o n o t o n s t e i g e n d$
Teilaufgabe c)
Tangente an $G_{f}$ im Berührpunkt B(3;f(3)).
$y_{B} = f (x_{B}) \Leftrightarrow f (3) = \frac{3^{2} - 1}{3^{2} + 1} = \frac{8}{10}$
Die Tangente ist eine Gerade, daher: $y = m \cdot x + b$ .
Die Steigung m ist der Wert der 1. Ableitung an der Stelle $x_{B} = 3$ . $m = \frac{12}{10^{2}} = \frac{12}{100} = 0,12$ .
Somit $y = 0,12 \cdot x + b$ .
Die Koordinaten des Berührpunktes erfüllen die Tangentengleichung.
Man setzt die Koordinaten des Berührpunktes in die Tangentengleichung ein und erhält den y-Achsenabschnitt b.
$\frac{8}{10} = \frac{12}{100} \cdot 3 + b \Rightarrow b = \frac{8}{10} - \frac{36}{100} = \frac{80}{100} - \frac{36}{100} = \frac{44}{100}$
Somit: t: $y = \frac{12}{100} \cdot x + \frac{44}{100}$
Winkelberechnung: $m = \tan (a) \Rightarrow a = 6,84 °$
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Nun wird die in $ℝ$ definierte Integralfunktion $F : x \mapsto \int_{0}^{x} f (t) d t$ betrachtet; ihr Graph wird mit $G_{F}$ bezeichnet.
a) Begründen Sie, dass $F$ in $x = 0$ eine Nullstelle hat, und machen Sie mithilfe des Verlaufs von $G_{f}$ plausibel, dass im Intervall $[1; 3]$ eine weitere Nullstelle von $F$ liegt. Geben Sie an, welche besondere Eigenschaft $G_{F}$ im Punkt $(- 1 | F (- 1))$ hat, und begründen Sie Ihre Angabe.
b) Die Gerade mit der Gleichung $y = x - 1$ begrenzt gemeinsam mit den Koordinatenachsen ein Dreieck. Geben Sie den Flächeninhalt dieses Dreiecks und den sich daraus ergebenden Näherungswert für $F (1)$ an.
c) Die Abbildung 2 zeigt den Graphen $G_{f}$ sowie den Graphen $G_{g}$ der in $ℝ$ definierten Funktion
$g : x \mapsto - \cos (\frac{π}{2} x)$ .
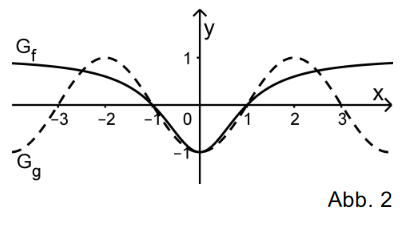
Beschreiben Sie, wie $G_{g}$ aus dem Graphen der in $ℝ$ definierten Funktion $x \mapsto \cos x$ hervorgeht, und berechnen Sie durch Integration von $g$ einen weiteren Näherungswert für $F (1)$ .
(zur Kontrolle: $F (1) \approx - \frac{2}{π}$ )
d) Berechnen Sie das arithmetische Mittel der beiden in den Aufgaben 2b und 2c berechneten Näherungswerte. Skizzieren Sie den Graphen von $F$ für $0 \leq x \leq 3$ unter Berücksichtigung der bisherigen Ergebnisse in der Abbildung 1.
Teilaufgabe a)
$F : x \to F (x) = \int_{o}^{x} f (t) d t$
hat an der Stelle $x_{0}$ =0 eine Nullstelle, da untere und obere Grenze des Integrals gleich sind.
Im Intervall $[1; 3]$ liegt eine weitere Nullstelle, wenn man einen Vorzeichenwechsel von $F$ in diesem Intervall nachweisen kann.
$F (1) = \int_{0}^{1} f (t) d t < 0$ ,
Im Intervall $[0; 1 [$ liegt der Graph $G_{f}$ unterhalb der $x$ -Achse. Somit ist der Integrand $f (t)$ in diesem Intervall negativ. Damit gilt auch $F (1) < 0$ .
Da der Graph $G_{f}$ in diesem Intervall gut durch eine Gerade mit dem $x$ -Achsen Abschnitt $x_{0} = 1$ und dem $y$ -Achsenabschnitt $y_{0} = - 1$ angenähert wird, kann man den Wert von $F (1)$ mit $- \frac{1}{2}$ abschätzen.
$F (3) = \int_{0}^{3} f (t) d t = \int_{0}^{1} f (t) d t + \int_{1}^{3} f (t) d t$
Auf Grund der vorgegebenen Skizze des Graphen $G_{f}$ kann man
$\int_{1}^{3} f (t) d t$ mit etwa $\frac{3}{4}$ abschätzen.
Damit ergibt sich für $F (3) = - \frac{1}{2} + \frac{3}{4} > 0$ .
Also hat $F$ neben $x_{0} = 0$ im Intervall $[1; 3]$ eine weitere Nullstelle.
Im Punkt $P (- 1 | F (- 1))$ liegt ein Maximum (Hochpunkt) des Graphen $G_{F}$ .
Begründung: Der Graph $G_{f}$ stellt die 1. Ableitung von $F$ da.
Aus dem Graph $G_{f}$ liest man ab:
Für $x < - 1$ gilt: $f (x) > 0 \Rightarrow F$ wachsend.
für $- 1 < x < 1$ gilt: $f (x) < 0 \Rightarrow F$ fallend.
Teilaufgabe b)
Die Gerade $y = x - 1$ begrenzt mit den Koordinatenachsen ein Dreieck.
Dieses Dreieck ist rechtwinklig mit den Kathetenlängen $a = b = 1 \Rightarrow$
$A_{Δ} = \frac{1}{2} \cdot 1 \cdot 1 = \frac{1}{2} \Rightarrow F (1) = \frac{1}{2} F E$
Teilaufgabe c)
$g (x) = - \cos (\frac{π}{2} x)$
Im Vergleich zur Grundfunktion $a (x) = \cos (x)$ ist die Periode von $g$ verändert.
Für die Periode von $g$ gilt: $p = \frac{2 π}{\frac{π}{2}} = \frac{2 π \cdot 2}{π} = 4$ .
Falls man diese Regel nicht parat hat, so hat man zwei Möglichkeiten:
Aus dem Graphen $G_{g}$ kann man ablesen, dass $x_{0} = - 1$ und $x_{1} = 1$ benachbarte Nullstellen sind. Also wäre $\frac{p}{2} = 2 \Rightarrow p = 4$
Oder man erinnert sich, dass $f (x) = \sin (2 \cdot x)$ die Periode $p = π$ hat. Und allgemein gilt: $f (x) = \sin (a \cdot x)$ hat die Periode $p = \frac{2 π}{a}$
Zusätzlich zur Periodenänderung wird der Graph noch an der $x$ -Achse gespiegelt.
Näherungswert für $F (1)$ :
$F (1) = \int_{0}^{1} [- \cos (\frac{π}{2} \cdot x) d x = - \frac{2}{π} \int_{0}^{1} \cos (\frac{π}{2} \cdot x) \cdot \frac{π}{2} d x ⟺$
$F (1) = - \frac{2}{π} \cdot \sin (\frac{π}{2} \cdot x) |_{0}^{1} = - \frac{2}{π} \cdot [\sin (\frac{π}{2}) - \sin (0)] = - \frac{2}{π} \cdot [1 - 0] = - \frac{2}{π}$
Teilaufgabe d)
arithmetisches Mittel aus den beiden Näherungswerten:
$m = \frac{\frac{- 1}{2} + \frac{- 2}{π}}{2} \approx - \frac{1,137}{2} \approx - 0,57$
Die Funktion von $F$ hat an der Stelle $x = - 1$ eine Maximumstelle.
Da die Funktion f, wie in a) gezeigt, achsensymmetrisch ist, ist $F$ als Integralfunktion zu $f$ punktsymmetrisch, weil, wie in 2a) gezeigt, $F (0) = 0$ gilt.
Somit hat $F$ an der Stelle $x = 1$ eine Minimumstelle.
Es gilt nämlich:
Ist $f$ achsensymmetrisch, so ist $F$ punktsymmetrisch, falls $F (0) = 0$ ist.
Achsensymmetrie: $f (x) = f (- x)$ für alle $x$ (*)
Punktsymmetrie: $F (x) = - F (- x)$ für alle $x$
Wir definieren $F (x) = \int_{0}^{x} f (t) d t$ und verwenden die Substitutionsregel:
$t = g (u) = - u$ . Dann ist $u = - t$ und es gilt:
$t = 0 ⟺ u = 0$ und $t = x ⟺ u = - x$ .
Außerdem ist $g^{'} (u) = - 1.$
$F (x) = \int_{0}^{x} f (t) d t = \int_{0}^{- x} f (u) (- 1) d u = - \int_{0}^{- x} f (u) d u = - F (- x)$
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Für jeden Wert $k > 0$ legen die auf $G_{f}$ liegenden Punkte $P_{k} (- k | f (- k))$ und $Q_{k} (k | f (k))$ gemeinsam mit dem Punkt $R (0 | 1)$ ein gleichschenkliges Dreieck $P_{k} Q_{k} R$ fest.
a) Berechnen Sie für $k = 2$ den Flächeninhalt des zugehörigen Dreiecks $P_{2} Q_{2} R$ (vgl. Abbildung 3).
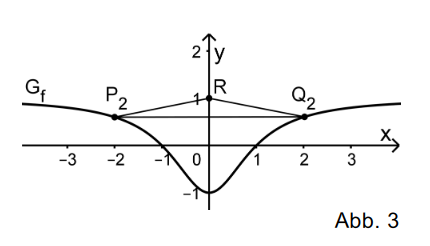
Zeigen Sie anschließend, dass der Flächeninhalt des Dreiecks $P_{k} Q_{k} R$ allgemein durch den Term $A (k) = \frac{2 k}{k^{2} + 1}$ beschrieben werden kann.
b) Zeigen Sie, dass es einen Wert von $k > 0$ gibt, für den $A (k)$ maximal ist. Berechnen Sie diesen Wert von $k$ sowie den Flächeninhalt des zugehörigen Dreiecks $P_{k} Q_{k} R$ .

Teilaufgabe a)
$k = 2$ . $f (x) = \frac{x^{2} - 1}{x^{2} + 1} \Rightarrow f (2) = \frac{2^{2} - 1}{2^{2} + 1} = \frac{3}{5}$
Damit $P_{2} (- 2; \frac{3}{5}) Q_{2} (2; \frac{3}{5})$ $R (0; 1)$
Die Grundseite g des Dreiecks ist die Strecke $P_{2} Q_{2}$ .
Somit gilt für die Grundseite $g = 4.$
Die Höhe h ist die Strecke zwischen dem Punkt R und der y-Koordinate von $P_{2}$ .
Somit gilt für die Höhe $h = 1 - \frac{3}{5} = \frac{2}{5} .$
Also berechnet sich der Flächeninhalt des Dreiecks $R P_{2} Q_{2}$ zu: $A (2) = \frac{1}{2} \cdot 4 \cdot \frac{2}{5} = \frac{4}{5} F E$ .
Im allgemeinen Fall gilt für die Grundseite $g = 2 \cdot k$ und für die Höhe $h = 1 - f (k) = 1 - \frac{k^{2} - 1}{k^{2} + 1} = \frac{(k^{2} + 1 - [k^{2} - 1])}{k^{2} + 1}$
Also $h = \frac{k^{2} + 1 - k^{2} + 1}{k^{2} + 1} = \frac{2}{k^{2} + 1}$ .
Für den Flächeninhalt gilt dann:
$A {(k)}_{} = \frac{1}{2} \cdot 2 \cdot k \cdot \frac{2}{k^{2} + 1} = \frac{2 k}{k^{2} + 1}$ .
Teilaufgabe b)
Zeige, dass es ein $k > 0$ gibt, so dass $A (k)$ maximal wird.
Mit Hilfe der 1.Ableitung von $A (k)$ sucht man eine Maximumstelle.
$A^{'} (k) = 2 \cdot \frac{(1 \cdot (k^{2} + 1) - k \cdot 2 \cdot k)}{{(k^{2} + 1)}^{2}} = 2 \cdot \frac{(k^{2} + 1 - 2 k^{2})}{{(k^{2} + 1)}^{2}}$
$A^{'} (k) = 2 \cdot \frac{(1 - k^{2})}{{(k^{2} + 1)}^{2}}$ .
$A^{'} (k) = 0 \Leftrightarrow 1 - k^{2} = 0 \Leftrightarrow k^{2} = 1 \Leftrightarrow k = 1$ , da $k > 0$ . Das Vorzeichen von $A^{'} (k)$ wird nur vom Zähler $z = 1 - k^{2}$ bestimmt. Denn der Nenner ist als Quadrat nicht negativ.
Graphisch dargestellt ist $z$ eine nach unten geöffnete Normalparabel um 1 nach oben verschoben.
Somit ändert $A^{'} (k)$ an der Stelle $k = 1$ das Vorzeichen von plus zu minus. Also ist $k = 1$ Maximumstelle.
Damit ergibt sich für den maximalen Flächeninhalt:
$A_{\max} = 2 \cdot \frac{1}{(1^{2} + 1)} = \frac{2}{2} = 1 F E .$