1 Überblick
Das Geschwisterparadoxon oder Junge-oder-Mädchen-Problem ist eine spannende Fragestellung aus der Stochastik und wird ohne mathematische Simulation oder Berechnung meistens falsch gelöst.
In diesem Kurs lernst du Schritt für Schritt, wie du ohne viel Vorwissen das Geschwisterparadoxon in einer Tabellenkalkulationssoftware (z.B. das kostenfreie LibreOffice Calc) simulieren und so die gestellte Frage leicht beantworten kannst.
Wenn du selbst mitmachen möchtest, brauchst du:
Ein Programm zur Tabellenkalkulation
2 Das Geschwister-Paradoxon
Du ziehst neu in ein Haus ein und siehst zum ersten Mal deine Nachbarin gemeinsam mit ihrem Sohn.
Ihr kommt ins Gespräch und sie verrät dir, dass sie noch ein zweites Kind zu Hause hat. Du versäumst allerdings, sie zu fragen, ob das zweite Kind ein Junge oder ein Mädchen ist.
Du überlegst: "Die Wahrscheinlichkeit dafür, dass die Mutter zwei Söhne hat, ist genauso groß wie die Wahrscheinlichkeit, dass sie einen Sohn und eine Tochter hat. Oder!?"
Doch je länger du darüber nachdenkst, desto unsicherer wirst du dir. Du entscheidest dich, die Situation zu simulieren und dabei deine Fähigkeiten im Umgang mit Tabellenkalkulationssoftware aufzufrischen.

3 Fragestellung beachten!
Vielleicht hast du dir die letzte Seite durchgelesen und dachtest dir sofort:
"Natürlich ist es gleich wahrscheinlich bei einer Geburt einen Jungen oder ein Mädchen zu gebären! (Die Statistik sagt hier zu )"
Das war aber nicht die Fragestellung. In der Stochastik ist es häufig wichtig, genau zu lesen und sich den Ergebnisraum zu überlegen.
Es geht um die Konstellation der beiden Geschwister.
Mögliche Ergebnisse sind: Es sind zwei Jungen, es ist ein Junge und ein Mädchen und (unmöglich, da du den einen Sohn bereits gesehen hast) es sind zwei Mädchen.
_
[1] https://royalsocietypublishing.org/doi/10.1098/rspb.2019.2849, aufgerufen am 10.12.2020
4 Simulationen mit Tabellenkalkulation
Da Tabellenkalkulationssoftware schnell und einfach dazu verwendet werden kann, Zufallszahlen zu erzeugen und anschließend zu analysieren, ist sie für Simulationen besonders gut geeignet.
Am besten kommt das Programm natürlich mit Zahlen klar. Deshalb sind Fragestellungen wie "Mädchen oder Junge?" am einfachsten zu beantworten, wenn man zuvor den Ergebnisraum zu Zahlen verändert. Ab jetzt gilt deshalb:
Ein Mädchen ist in der Simulation die Zahl 1.
Ein Junge ist in der Simulation die Zahl 0.
5 Familien erzeugen
Natürlich kann man viele Tausende Eltern mit zwei Kindern befragen, allerdings ist das sehr aufwändig und dadurch, dass man weiß, dass die Geburten von Mädchen und Jungen ungefähr gleichwahrscheinlich sind, kann ein Tabellenkalkulationsprogramm die "Befragung" simulieren.
Auftrag:
Öffne das Tabellenkalkulationsprogramm und schreibe in die Zelle A1 "1. Kind" und in B1 "2. Kind".
Suche eine Formel, die dir zufällig die Zahl 0 (Junge) oder 1 (Mädchen) ausgibt und kopiere diese Formel sowohl in A2 als auch in B2.
Wähle die beiden Zellen gemeinsam aus und kopiere die Formel bis zur Zeile 501 nach unten.
So hast du schnell 500 Familien mit zwei Kindern erzeugt!
6 Familienanalyse vorbereiten
Nun kannst du die Familienkonstellationen genauer betrachten.
Auftrag:
Überlege dir, wie die beiden Zahlen sinnvoll kombiniert werden können, um so die Familiensituation durch eine Zahl zu beschreiben.
Ergänze in deinem Rechenblatt in Spalte C die passende Berechnung.
7 Unmögliche Fälle entfernen
Du weißt bereits, dass deine Nachbarin einen Sohn hat. Da sie nur zwei Kinder hat, kann sie nicht zwei Töchter haben.
Aus deinen Testfamilien zählst du also nur die zur Stichprobe, die mindestens einen Jungen in der Familie haben.
Auftrag:
Schreibe in E2 den Text "befragte Familien" und finde eine Möglichkeit, alle gültigen Familienstände aus Spalte C aufzusummieren.
8 absolute Häufigkeiten ermitteln
Die Antwort ist nahe!
Auftrag:
Schreibe in die Zelle E4 "Familien mit Schwester" und in E5 "Familien mit Bruder.
Überlege dir, wie du aus den Einträgen in der Spalte C die Anzahl der Familien mit einem Bruder und einer Schwester ermitteln kannst. Schreibe die Formel in F4.
Überlege dir, wie du aus den bisherigen Ergebnissen die Familien mit zwei Söhnen ermitteln kannst. Schreibe die Formel in F5.
9 relative Häufigkeiten ermitteln
Um die Situation sinnvoll zu analysieren, kannst du die Prozentzahlen ermitteln und nachforschen, ob diese einen Zusammenhang sichtbar machen.
Auftrag
Ergänze z.B. in den Zellen G4 und G5 den Anteil der Familien mit Sohn-Tochter beziehungsweise Sohn-Sohn. Formatiere die Zahlen (z.B. mit Rechtsklick> Zellen formatieren) als Prozentzahl.
10 noch nicht genau genug?
Glaubst du dem Rechenblatt noch immer nicht?
Die Simulation mit dem Tabellenkalkulationsprogramm ermöglicht es dir, einfach weitere Familien hinzuzufügen.
Auftrag
Ziehe den Inhalt der Zellen A2 bis C2 bis zur Zeile 2001 herunter und aktualisiere die Zellen F2 und F4 (ggf. F5, G4, G5) entsprechend.
11 Deutung der relativen Häufigkeiten
Nach dem Gesetz der großen Zahlen nähert sich die relative Häufigkeit bei einer sehr großen Stichprobe der Wahrscheinlichkeit für ein bestimmtes Ereignis an.
Dass ca. der Familien einen Sohn und eine Tochter haben, macht es also wahrscheinlicher, dass die Nachbarin ebenfalls einen Sohn und eine Tochter hat und nicht zwei Söhne.

12 Doch woher kommen die 67 %?
Es sieht gerade so aus, als wären die Geburten doch nicht gleich wahrscheinlich. Betrachtet man allerdings alle Kombinationen, die es für zwei Geschwister gibt, so lässt sich die Zahl einfach erklären.
{
(1. Kind: Junge, 2. Kind: Junge),
(1. Kind: Junge, 2. Kind: Mädchen),
(1. Kind: Mädchen, 2. Kind: Junge),
(1. Kind: Mädchen, 2. Kind: Mädchen)}
Jedes dieser vier Ergebnisse ist gleich wahrscheinlich () und unterscheidet sich von den anderen.
Dadurch, dass wir mindestens einen Sohn in der Familie haben wollen, gibt es aber nur noch drei Ergebnisse.
(1. Kind: Junge, 2. Kind: Junge),
(1. Kind: Junge, 2. Kind: Mädchen),
(1. Kind: Mädchen, 2. Kind: Junge)}
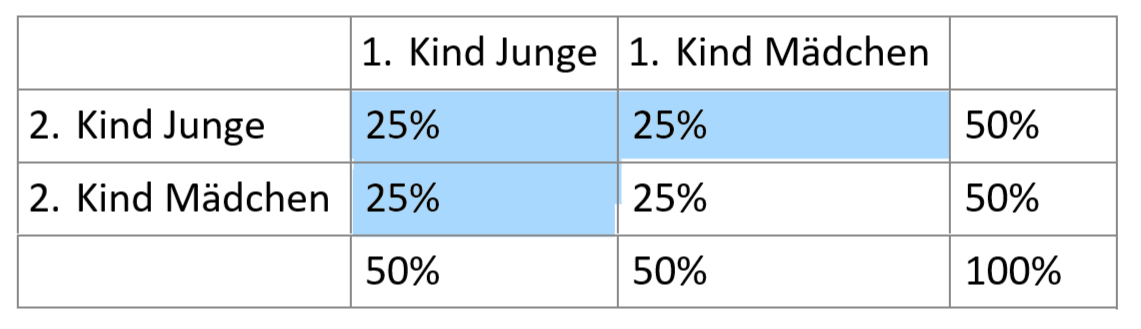
nur noch die blau markierten Familien werden betrachtet. Das sind 75 % der Familien
enthält nur noch aller Familien, die der Familien mit zwei Töchtern gibt es nicht mehr. Für deine alltägliche Fragestellung hast du den Ergebnisraum selbst zusätzlich vergröbert, also weniger genau hingeschaut und die gemischten Familien zusammengefasst. Die der Familien mit einem Jungen und einem Mädchen entsprechen bei der neuen Gesamtzahl an Familien der Familien, denn von sind . Das übrige Drittel sind die Familien mit zwei Söhnen.
Rechnerisch verbirgt sich hinter dieser Handlung, also der Einschränkung der Ergebnismenge, übrigens die bedingten Wahrscheinlichkeit.
13 Vertiefung
Die Nachbarin sagt dir, dass der Sohn, den du siehst, das erstgeborene Kind ist.
Wie verändert das die Situation, dein Rechenblatt, die Ergebnismenge und die Wahrscheinlichkeit?
Schreibe es doch in die Kommentare!
