Pfadregeln

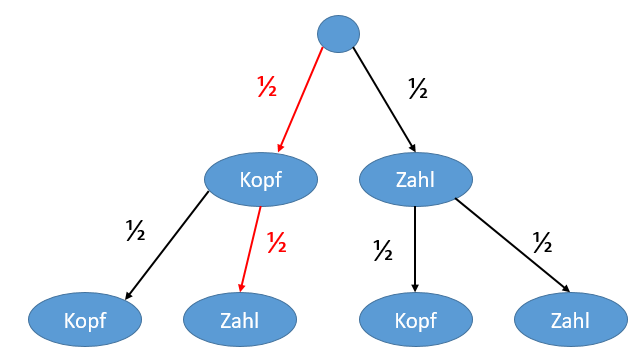
1.Pfadregel (Produktregel)

Um die Wahrscheinlichkeit für einen ganz bestimmten Versuchsausgang zu erhalten, müssen die Wahrscheinlichkeiten entlang des jeweiligen Pfades multipliziert werden.

Die Wahrscheinlichkeit des Ereignisses A (kurz P(A)), dass bei zweimaligem Münzwurf mit einer perfekten Münze zuerst Kopf und dann Zahl geworfen wird, lässt sich mithilfe der 1. Pfadregel berechnen durch:

2. Pfadregel (Summenregel)

Soll die Wahrscheinlichkeit eines Ereignisses, das mehrere Versuchsausgänge umfasst, berechnet werden, müssen die Wahrscheinlichkeiten der einzelnen Versuchsausgänge addiert werden.

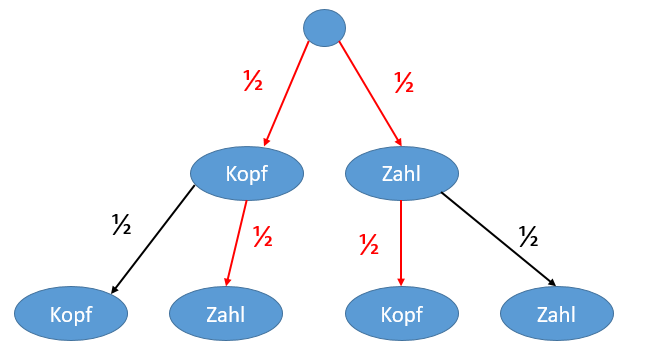
Die Wahrscheinlichkeit des Ereignisses B="genau einmal wird Kopf geworfen" umfasst die beiden Versuchsausgänge "Kopf-Zahl" und "Zahl-Kopf". Die Wahrscheinlichkeiten dieser Ereignisse können laut der 2. Pfadregel addiert werden:

3.Pfadregel (Knotenregel)

Ausgehend von einem Knoten ergibt die Wahrscheinlichkeit der Ereignisse immer 1.

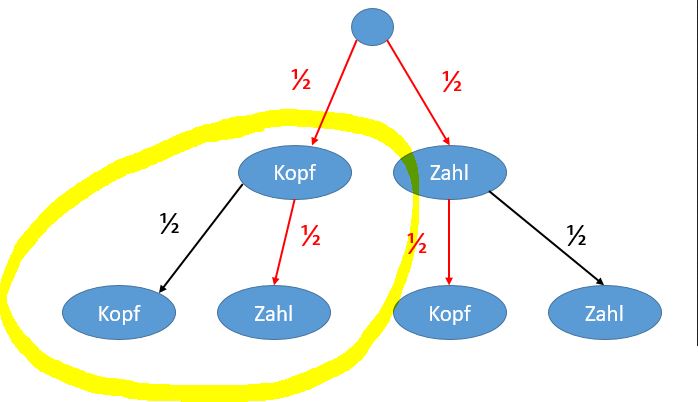
Ausgehend vom Knoten "Kopf" sind wieder die Ereignisse "Kopf" und "Zahl" möglich. Die Wahrscheinlichkeit beider Ereignisse zusammen ergibt 1.

Mithilfe dieser Regel lassen sich auch unbekannte Wahrscheinlichkeiten berechnen und sie gilt als gute Stütze, wenn es darum geht, das Baumdiagramm beim "Ziehen ohne Zurücklegen" aufzustellen.

Beispiele

Beispiel 1: Zweimaliges Werfen eines Würfels

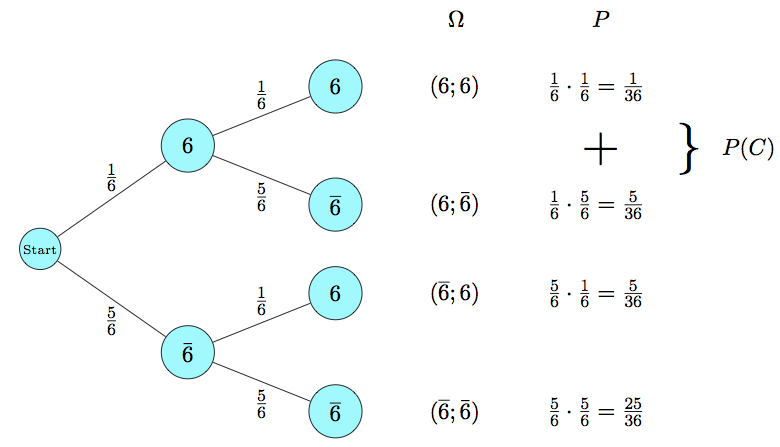
Die Wahrscheinlichkeit für C="zweimal 6" lässt sich mit der 1. Pfadregel aus dem Baumdiagramm berechnen:

$P\left(C\right)=\frac{1}{6}\cdot\frac{1}{6}=\frac{1}{36}$

Mithilfe beider Pfadregeln lässt sich auch die Wahrscheinlichkeit des Ereignisses D="zuerst eine 6" berechnen:

$\def\arraystretch{1.25} \begin{array}{l}P\left(D\right)=P\left(\left\{\left(6;\overline6\right);\left(6;6\right)\right\}\right)=\frac5{36}+\frac1{36}=\frac16\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\end{array}$

Beispiel 2: Zweimaliges Ziehen ohne Zurücklegen

Zweimaliges Ziehen von Losen ohne Zurücklegen, die entweder Treffer oder Niete sein können. Es gibt 20 Lose, von denen 5 Treffer sind.

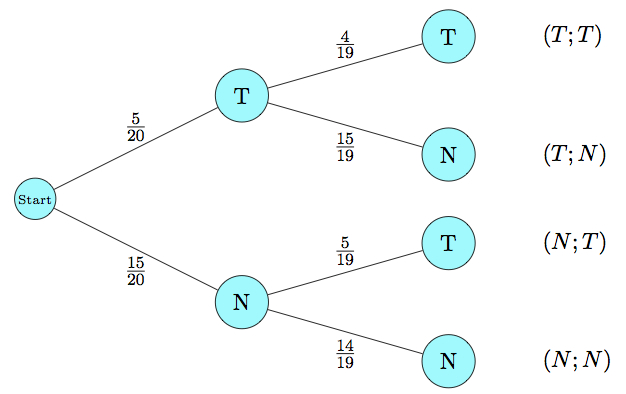
Berechnung der Wahrscheinlichkeit für zwei Treffer:

Mit $E=\left\{\left(T;T\right)\right\}$  gilt:

Erklärung:

Nach dem ersten Ziehen stehen nicht mehr 20, sondern nur noch 19 Lose zur Verfügung. Deshalb ändert sich der Nenner.

Berechnung der Wahrscheinlichkeit für "Höchstens einmal Niete":

Mit  $A=\left\{\left(T;T\right),\;\left(T;N\right),\left(N;T)\right)\right\}$  gilt unter Verwendung der zwei Pfadregeln: