Mehrstufige Zufallsexperimente sind Zufallsexperimente, die aus mehreren Schritten zusammengesetzt sind. Die einzelnen Schritte sind dabei selbst jeweils Zufallsexperimente.
Mehrstufige Zufallsexperimente werden auch als zusammengesetzte Zufallsexperimente bezeichnet.
Bei den einzelnen Teil-Experimenten, aus denen sich das mehrstufige Experiment zusammensetzt, kann es sich um mehrere Wiederholungen des gleichen Experiments handeln, oder um ganz verschiedenartige Experimente.
Ergebnismenge bei mehrstufigen Zufallsexperimenten
Als Ergebnismenge verwendet man bei mehrstufigen Zufallsexperimenten meist eine Menge, die sich aus den Ergebnismengen der einzelnen Teil-Experimente ergibt.
Beispiel
In einem (zweistufigen) Zufallsexperiment wird
erst aus einer Urne, in der sich rote, blaue und gelbe Kugeln befinden, eine Kugel gezogen,
Mögliche Ergebnismenge für das erste Teil-Experiment "Ziehen aus der Urne": .
und anschließend eine Münze geworfen.
Mögliche Ergebnismenge für das zweite Teil-Experiment "Werfen einer Münze": .

Als Ergebnismenge des zusammengesetzten Experimentes kann man dann wählen:
Baumdiagramm als Hilfsmittel
Wenn die vorkommenden Ergebnismengen nicht zu groß sind und das gesamte Experiment nicht aus zu vielen Stufen besteht, ist es oft sinnvoll, sich ein Baumdiagramm zu zeichnen.
Im obigen Beispiel mit der Urne und der Münze könnte das Baumdiagramm so aussehen:
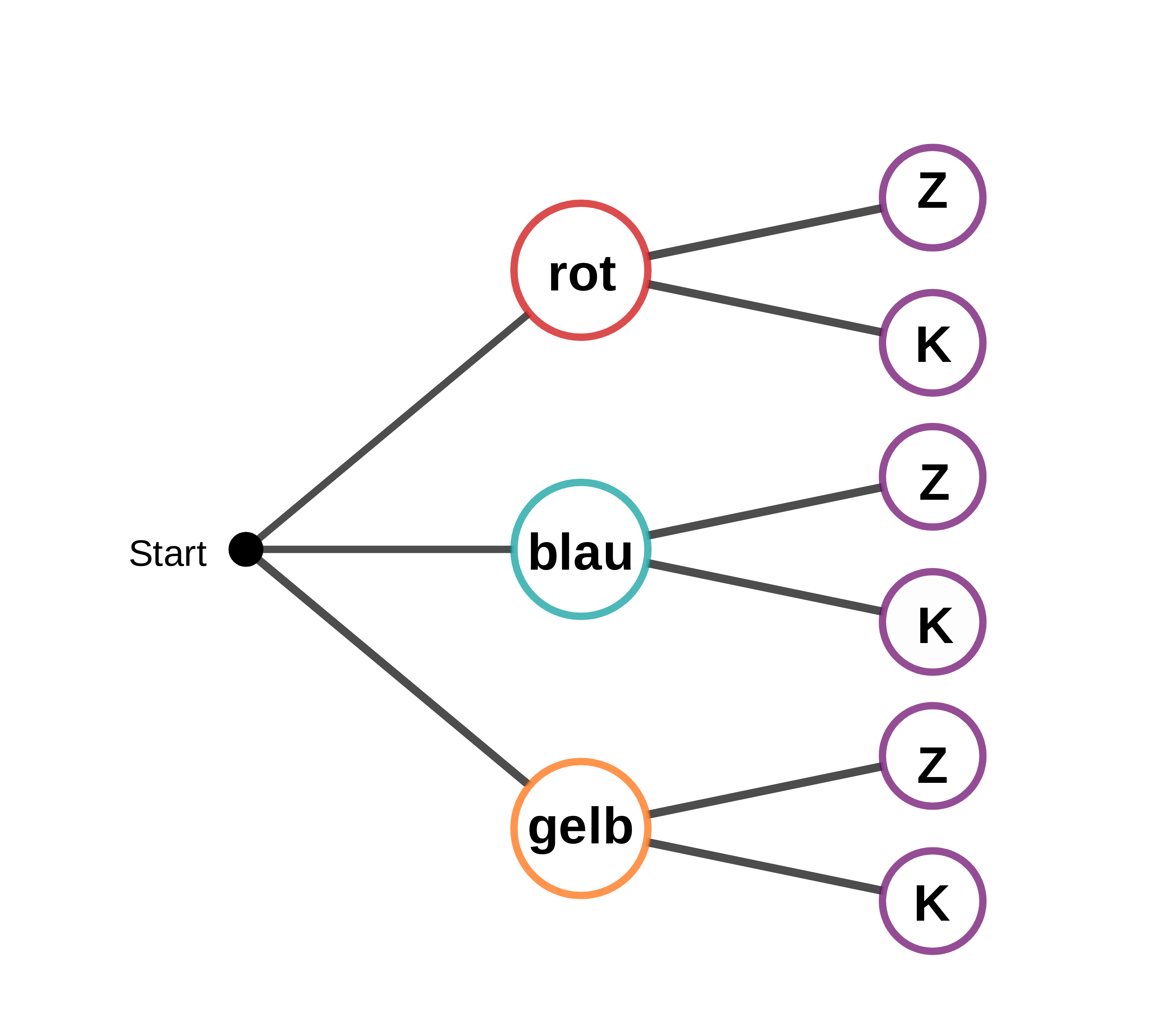
Wenn man das Baumdiagramm zu einem mehrstufigen Zufallsexperiment gezeichnet hat, kann man an den Endpunkten des Baumdiagramms die Elemente der Ergebnismenge ablesen oder ihre Anzahl abzählen.
Urnenmodell für "Standardfälle"
Wenn das Baumdiagramm so groß, dass man es nicht mehr zeichnen kann, kann man prüfen, ob stattdessen Methoden aus der Kombinatorik anwendbar sind.
Viele mehrstufige Zufallsexperimente lassen sich gut mit dem Urnenmodell darstellen.
Dabei wird das reale Zufallsexperiment modelliert durch das (mehrmalige) Ziehen von Kugeln aus einer Urne.
Dem Experiment "Dreimaliges Werfen eines Würfels" entspricht im Urnenmodell zum Beispiel das Experiment "Dreimaliges Ziehen mit Zurücklegen und mit Beachtung der Reihenfolge aus einer Urne mit 6 Kugeln."
Wahrscheinlichkeitsverteilung bei mehrstufigen Zufallsexperimenten
Wenn man Wahrscheinlichkeiten bei einem mehrstufigen Zufallsexperiment berechnen will, muss man sich dazu natürlich ebenfalls wieder die einzelnen Teilexperimente ansehen.
Wahrscheinlichkeiten im Baumdiagramm ermitteln
Wenn man für das mehrstufige Zufallsexperiment ein Baumdiagramm gezeichnet hat, kann man damit auch die Wahrscheinlichkeiten für das Gesamt-Experiment bestimmen.
Dazu verwendet man die Pfadregeln und berechnet so die gesuchte Wahrscheinlichkeit aus den Wahrscheinlichkeitsverteilungen der Teilexperimente.
Wahrscheinlichkeiten als Laplace-Wahrscheinlichkeiten
Falls die einzelnen Ergebnisse des zusammengesetzten Zufallsexperimentes alle gleichwahrscheinlich sind, kann man die Wahrscheinlichkeiten des mehrstufigen Zufallsexperiments als Laplace-Wahrscheinlichkeiten ausrechnen.
Die dazu benötigten Mächtigkeiten (der Ergebnismenge bzw. des betreffenden Ereignisses) bestimmte man oft mit Mitteln aus der Kombinatorik.
Quellen Bilder
"Urne mit einer roten, einer blauen und einer gelben Kugel": Eigene Darstellung
"Seite "Zahl" von 1-Euro-Münze": OpenClipart-Vectors auf Pixabay (https://pixabay.com/de/vectors/euro-m%C3%BCnze-w%C3%A4hrung-europa-geld-145386/)
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
