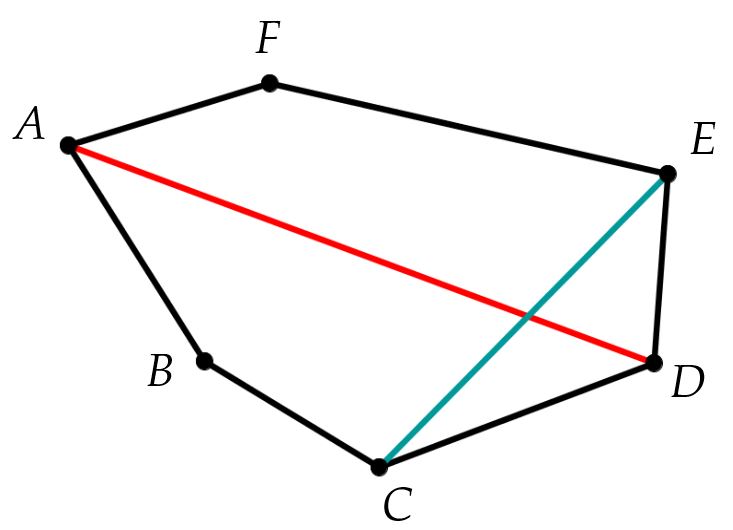
Eine Diagonale ist eine Strecke in einem Vieleck oder einem Körper, welche zwei nicht benachbarte Eckpunkte miteinander verbindet.
Beispiele:
ist eine Diagonale
ist eine Diagonale
ist zum Beispiel keine Diagonale, da und benachbarte Punkte sind.
Besondere Diagonalen
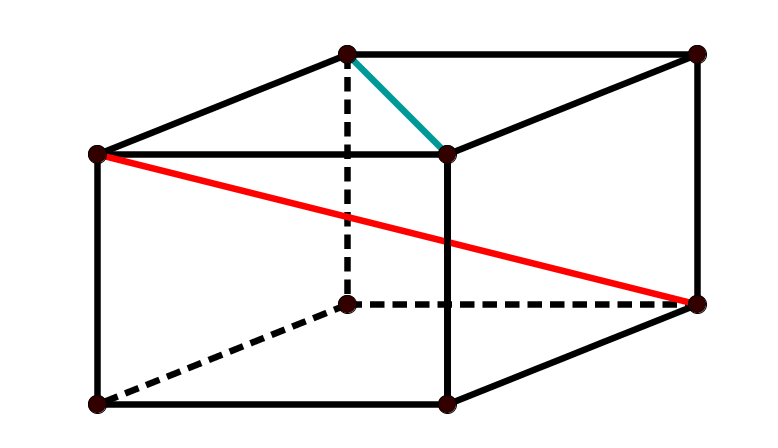
Besondere Diagonalen sind beispielsweise im Quader zu finden. Die Flächendiagonale, hier in , erstreckt sich diagonal über eine Rechtecksfläche. Sie taucht nicht nur einmal, sondern auf jeder Seite des Körpers zweimal auf. Im Beispiel rechts gibt es daher insgesamt vier Diagonalen, die die Länge der Linie haben.
Die Raumdiagonale, hier in , bildet die größte Strecke, die in einem Würfel oder Quader gezogen werden kann und erstreckt sich zum räumlich gegenüber liegenden Punkt. Genau in der Mitte zwischen den beiden Endpunkten liegt der Mittelpunkt des Körpers. Die Raumdiagonale ist ebenfalls mehrmals in Körpern zu finden.
Anzahl der Diagonalen in einem n-Eck
Man kann die Anzahl der Diagonalen in einem n-Eck mit folgender Formel ausrechnen
Damit gibt es in einem:
Dreieck: keine Diagonalen
Viereck: zwei Diagonalen
Fünfeck: fünf Diagonalen
usw.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
