Die Funktion beschreibt näherungsweise die zeitliche Entwicklung der Einwohnerzahl einer fränkischen Kleinstadt. Es gilt hierfür die Funktionsgleichung mit , .
Der Zeitpunkt wird auf den 1.1.1995 festgelegt. Dabei gibt n die Einwohnerzahl in Tausend und die Zeit in Jahren an. Auf Einheiten soll bei den Rechnungen verzichtet werden. Runden Sie die Ergebnisse sinnvoll.
Am 1.1.1999 hatte die Stadt Einwohner. Bestimmen Sie damit den Wert des Parameters b. (2 BE)
[ Ergebnis: ]
Berechnen Sie Art und Koordinaten des lokalen Extrempunktes des Graphen der Funktion n und interpretieren Sie Ihre Ergebnisse im gegebenen Sachzusammenhang. (7 BE)
[ mögliches Teilergebnis: ]
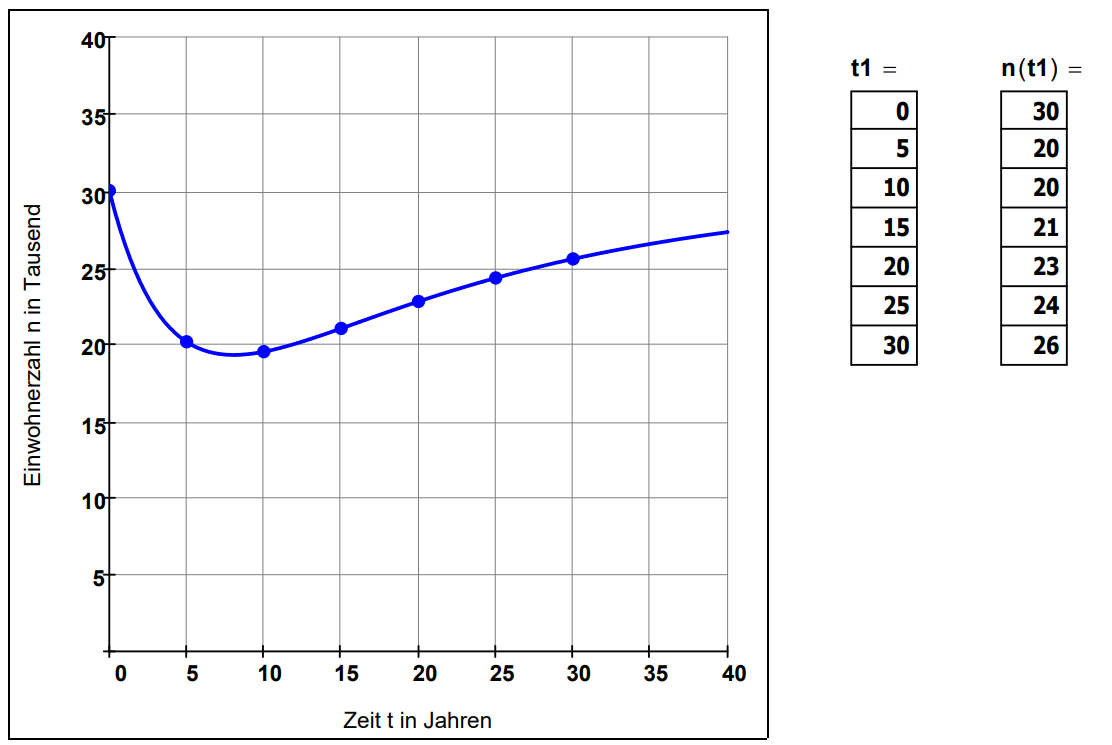
Zeichnen Sie den Graphen der Funktion n in ein geeignetes Koordinatensystem.
Zum 1.1.2010 konnte die Stadt Fördergelder beantragen. Diese richteten sich nach der durchschnittlichen Einwohnerzahl der Stadt während der vergangenen 15 Jahre. Ermitteln Sie die Höhe der Fördermittel, wenn es pro durchschnittlichem Einwohner an Fördergeldern gab, indem Sie zunächst das Integral berechnen. (5 BE)
[Teilergebnis: ]