1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, wie du ganze Zahlen multiplizierst.
Vorkenntnisse
Du solltest wissen, was ganze Zahlen sind.
Kursdauer
Dieser Kurs dauert etwa 25-30 min.
2 Wiederholung: Plus mal Plus
Plus mal Plus
Betrachte folgende Multiplikations-Tabelle natürlicher Zahlen:
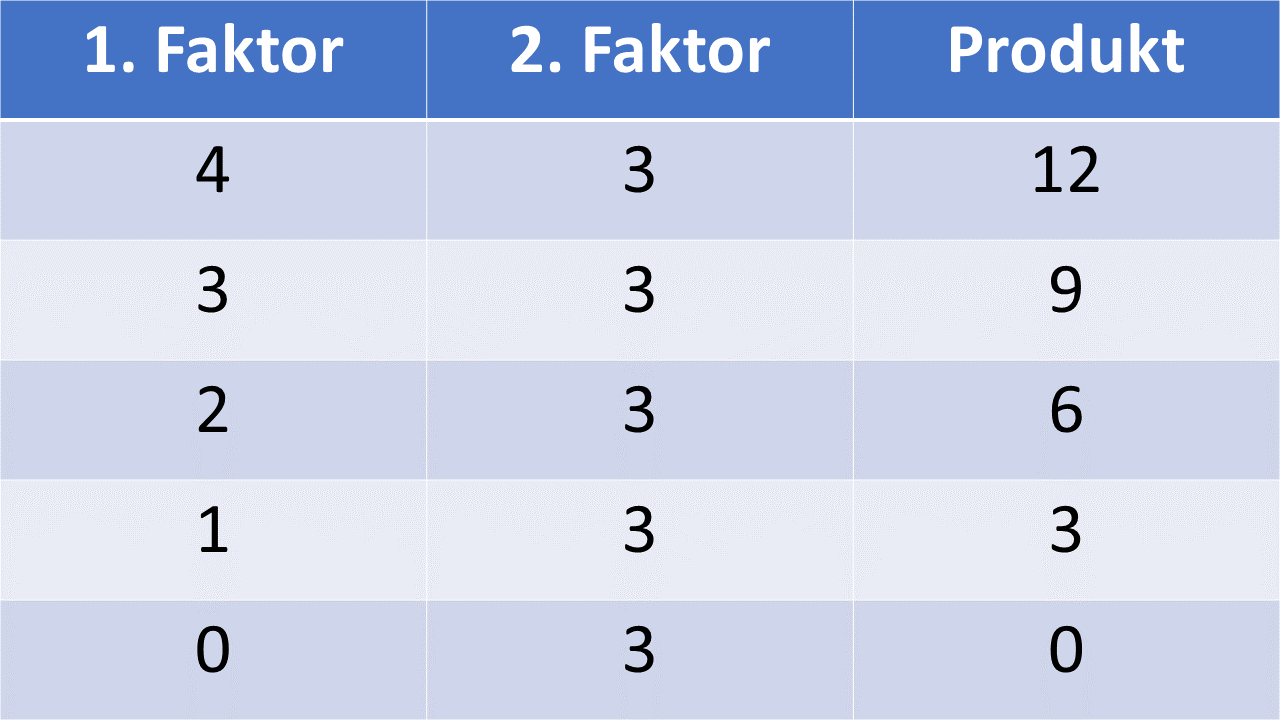
3 Minus mal Plus
Was aber ist ?
Wir können die Tabelle aus der vorherigen Kursseite weiter fortsetzen:
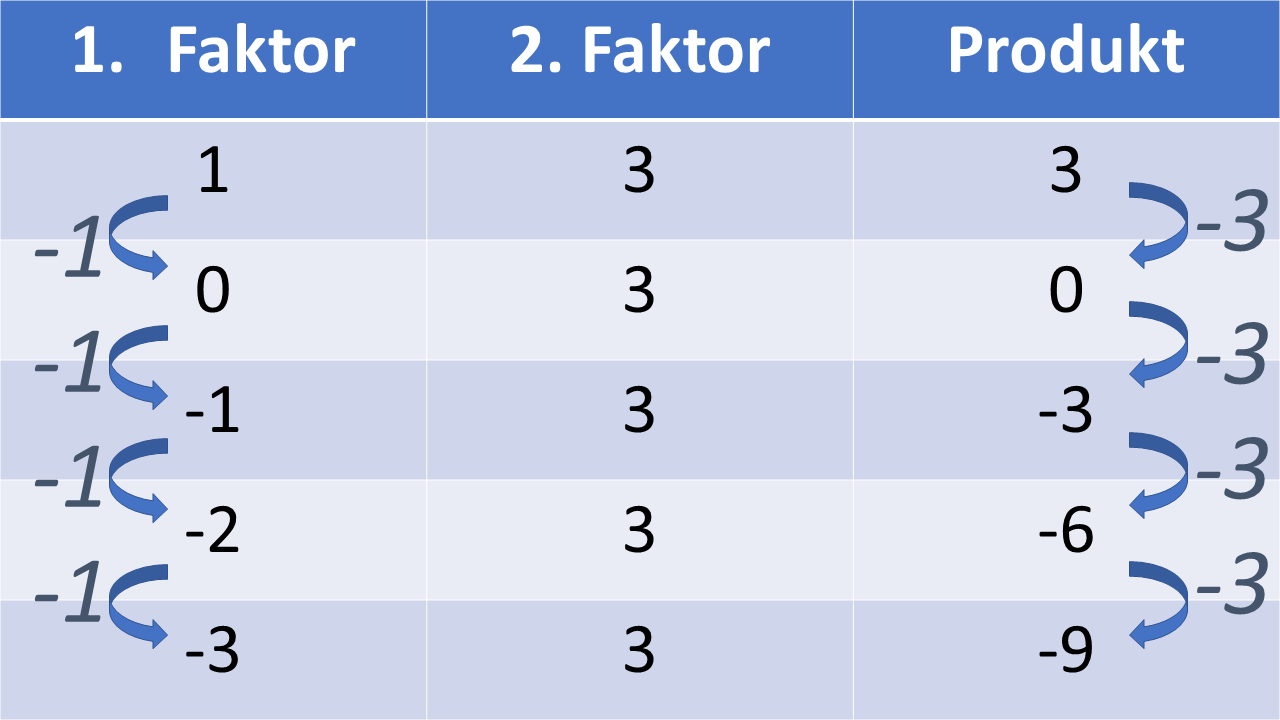
Man stellt also fest, dass .
Vergleiche mit dem bekannten Ergebnis von .
Auch für alle weiteren ganzen Zahlen funktioniert dieses Vorgehen.
So kannst du z.B. zeigen, dass und ; und usw.
Eine einfache Regel erleichtert dir das Multiplizieren einer negativen mit einer positiven Zahl.
4 Plus mal Minus
Du hast bereits das Kommutativgesetzes der Multiplikation kennengelernt. Das besagt:
In einem Produkt kann man die Faktoren in ihrer Reihenfolge beliebig vertauschen, ohne dass sich der Wert des Produkts ändert.
Dies gilt auch für ganze Zahlen. Du kannst also ohne Probleme rechnen:
| ↓ Kommutativgesetz | ||
| ↓ "" | ||
oder
| ↓ Kommutativgesetz | ||
| ↓ "" | ||
Die Regel "" lässt sich also auch leicht auf die Multiplikation von einer negativen mit einer positiven Zahl anpassen.
5 Minus mal Minus
Was passiert nun, wenn beide Faktoren eines Produktes negativ sind?
Ähnlich wie schon in der vorigen Aufgaben kannst du auch hier eine Multiplikations-Tabelle anlegen, die dir bei deinen Überlegungen hilft.
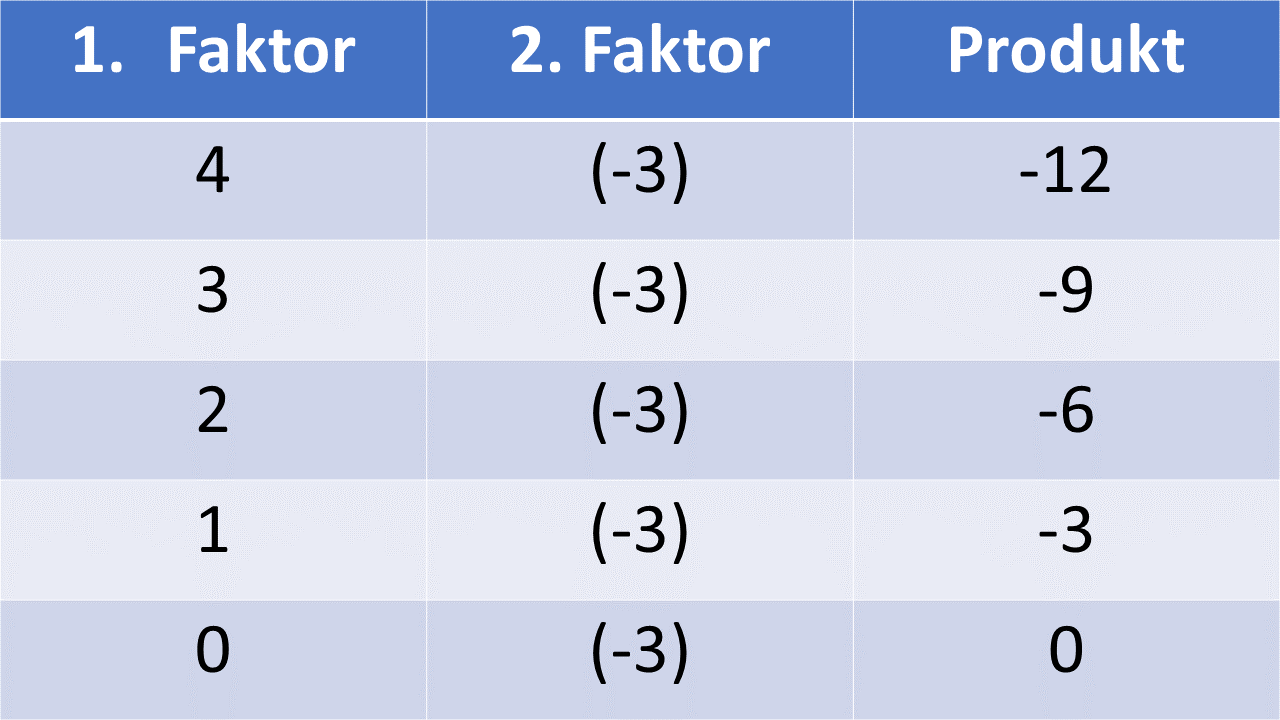
Man kann die Multiplikations-Tabelle also weiter fortsetzen:
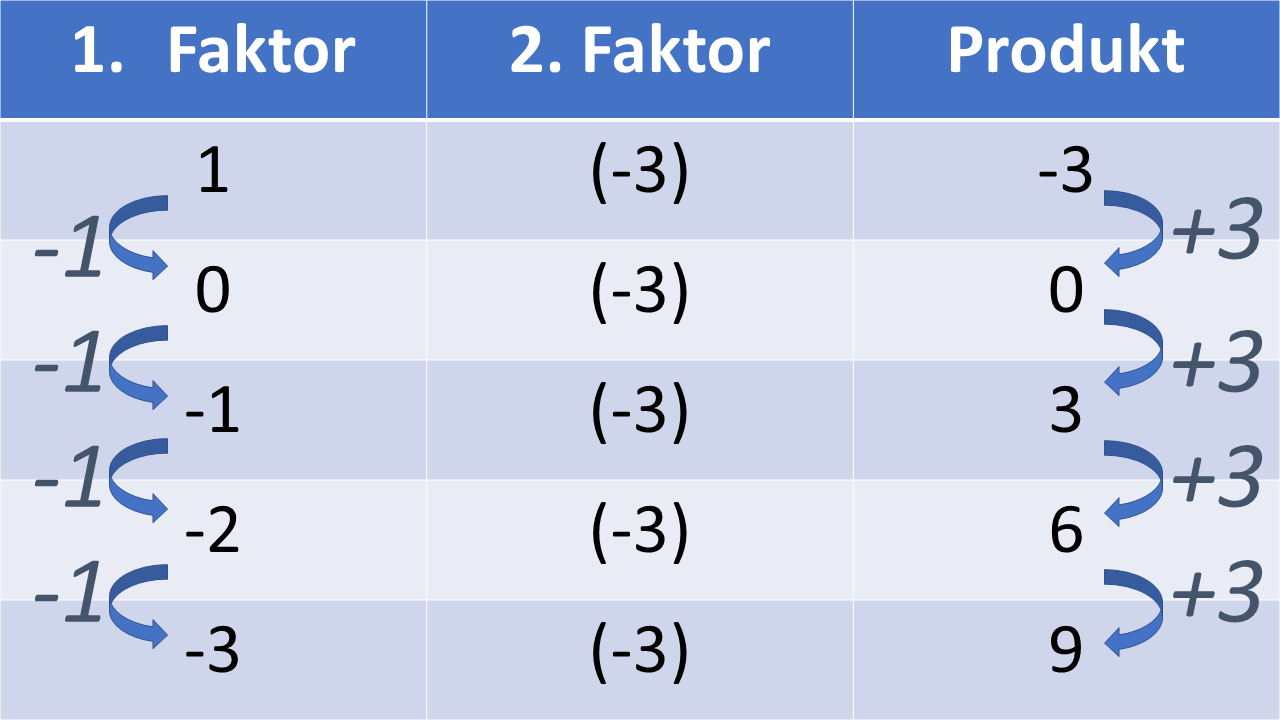
Es liegt nahe, das diesmal gilt: . Und so ist es auch!
Multipliziert man eine negative mit einer negativen Zahl, so ist das Ergebnis positiv.
6 Vorzeichentabelle
Aus deinen bisherigen Erkenntnissen lässt sich nun auch leicht eine sogenannte Vorzeichentabelle erstellen.
Wenn du zwei ganze Zahlen miteinander multiplizierst, kannst du mithilfe der Tabelle das Vorzeichen des Ergebnisses bestimmen:
Multiplikation | plus | minus |
|---|---|---|
plus | plus | minus |
minus | minus | plus |
7 Übungsaufgaben
Laden
Laden
Laden
Laden
Laden
Laden
Laden
Laden
