Aufgaben zu Spurpunkten einer Geraden
Wie gut kennst du dich aus? Vertiefe dein Wissen mit diesen Aufgaben zu den Spurpunkten und von Geraden.
- 1
Berechne die möglichen Spurpunkte der gegebenen Geraden.
Skizziere jeweils die Geraden und gib an, welche Lage die Geraden im Koordinatensystem haben.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Geraden
Spurpunkte berechnen
Um den Spurpunkt in der -Ebene zu berechnen, setzt man in der Geradengleichung und berechnet den Parameter :
↓ Setze .
Die erhaltene Gleichung ist für kein erfüllbar (falsche Aussage).
Somit gibt es keinen Spurpunkt in der -Ebene.
Für die Berechnung des Spurpunktes in der -Ebene setzt man in der Geradengleichung und berechnet den Parameter .
↓ Setze .
↓ Löse nach auf.
Der Wert wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der -Ebene zu berechnen:
↓ Setze ein.
↓ Vereinfache
Der Spurpunkt in der -Ebene hat die Koordinaten .
Für den Spurpunkt in der -Ebene setzt man in der Geradengleichung und berechnet den Parameter .
↓ Setze .
↓ Löse nach auf.
Der Wert wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der -Ebene zu berechnen:
↓ Setze ein.
Der Spurpunkt in der -Ebene hat die Koordinaten .
Skizze der Geraden
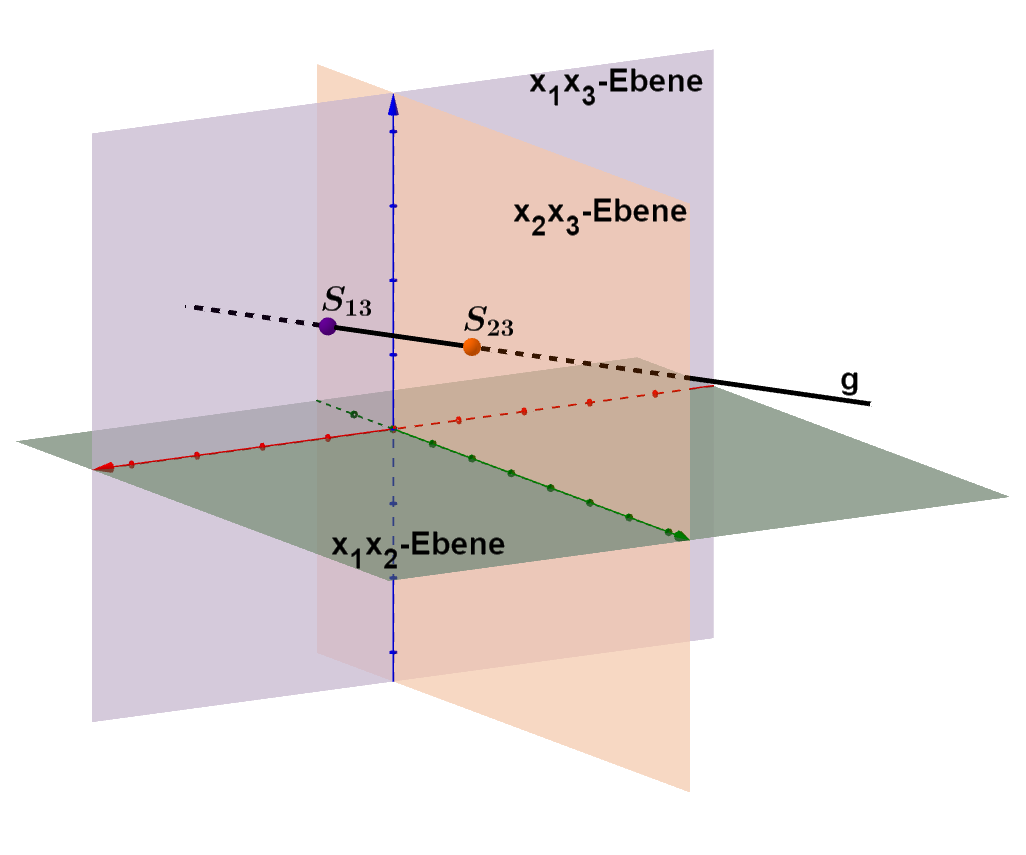
Lage der Geraden im Koordinatensystem
Die Gerade ist parallel zur -Ebene.

Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Geraden
Spurpunkte berechnen
Um den Spurpunkt in der -Ebene zu berechnen, setzt man in der Geradengleichung und berechnet den Parameter :
↓ Setze .
↓ Löse nach auf.
Der Wert wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der -Ebene zu berechnen:
↓ Setze ein.
↓ Vereinfache
Der Spurpunkt in der -Ebene hat die Koordinaten .
Für die Berechnung des Spurpunktes in der -Ebene setzt man in der Geradengleichung und berechnet den Parameter .
↓ Setze .
↓ Löse nach auf.
Der Wert wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der -Ebene zu berechnen:
↓ Setze ein.
↓ Vereinfache
Der Spurpunkt in der -Ebene hat die Koordinaten .
Für den Spurpunkt in der -Ebene setzt man in der Geradengleichung und berechnet den Parameter .
↓ Setze .
Der Wert wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der -Ebene zu berechnen:
↓ Setze ein.
↓ Vereinfache
Der Spurpunkt in der -Ebene hat die Koordinaten .
Skizze der Geraden
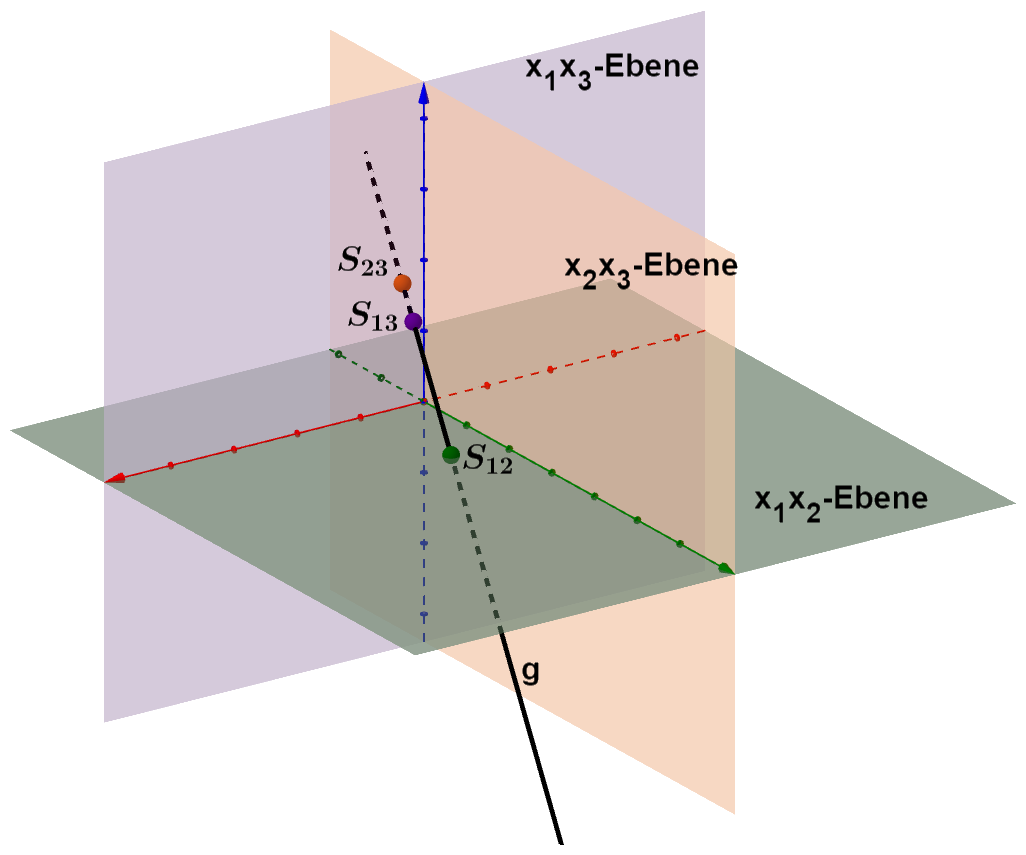
Lage der Geraden im Koordinatensystem
Die Gerade ist zu keiner Koordinatenebene parallel.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Geraden
Anhand der Geradengleichung kannst du feststellen, dass die Gerade durch den Koordinatenursprung verläuft. Sie ist außerdem zu keiner Koordinatenebene parallel. Es gibt somit nur einen Spurpunkt .
Skizze der Geraden
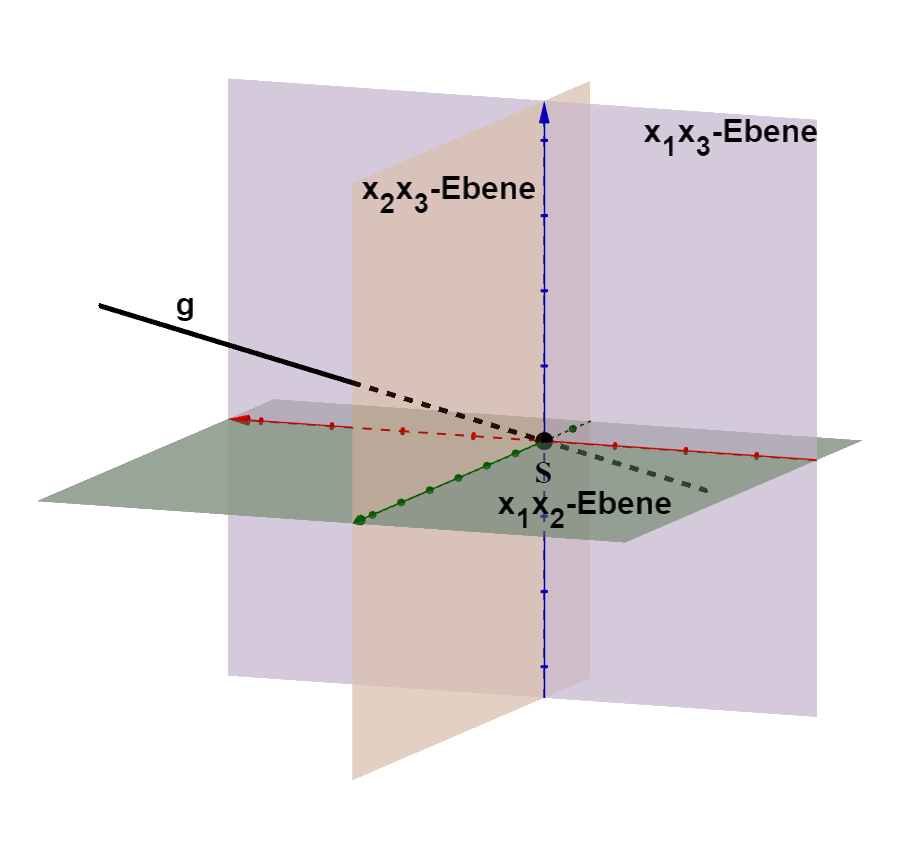
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Geraden
Spurpunkte berechnen
Um den Spurpunkt in der -Ebene zu berechnen, setzt man in der Geradengleichung und berechnet den Parameter :
↓ Setze .
Der Wert wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der -Ebene zu berechnen:
↓ Setze ein.
↓ Fasse zusammen.
Der Spurpunkt in der -Ebene hat die Koordinaten .
Für die Berechnung des Spurpunktes in der -Ebene setzt man in der Geradengleichung und berechnet den Parameter .
↓ Setze .
↓ Löse nach auf.
Der Wert wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der -Ebene zu berechnen:
↓ Setze ein.
↓ Fasse zusammen.
Der Spurpunkt in der -Ebene hat die Koordinaten .
Für den Spurpunkt in der -Ebene setzt man in der Geradengleichung und berechnet den Parameter .
↓ Setze .
Du hast die Gleichung erhalten. Diese Gleichung ist für alle erfüllt ( wahre Aussage). Die Gerade hat somit unendlich viele Schnittpunkte mit der -Ebene, d.h. die Gerade hat auch unendlich viele Spurpunkte in der -Ebene.
Skizze der Geraden
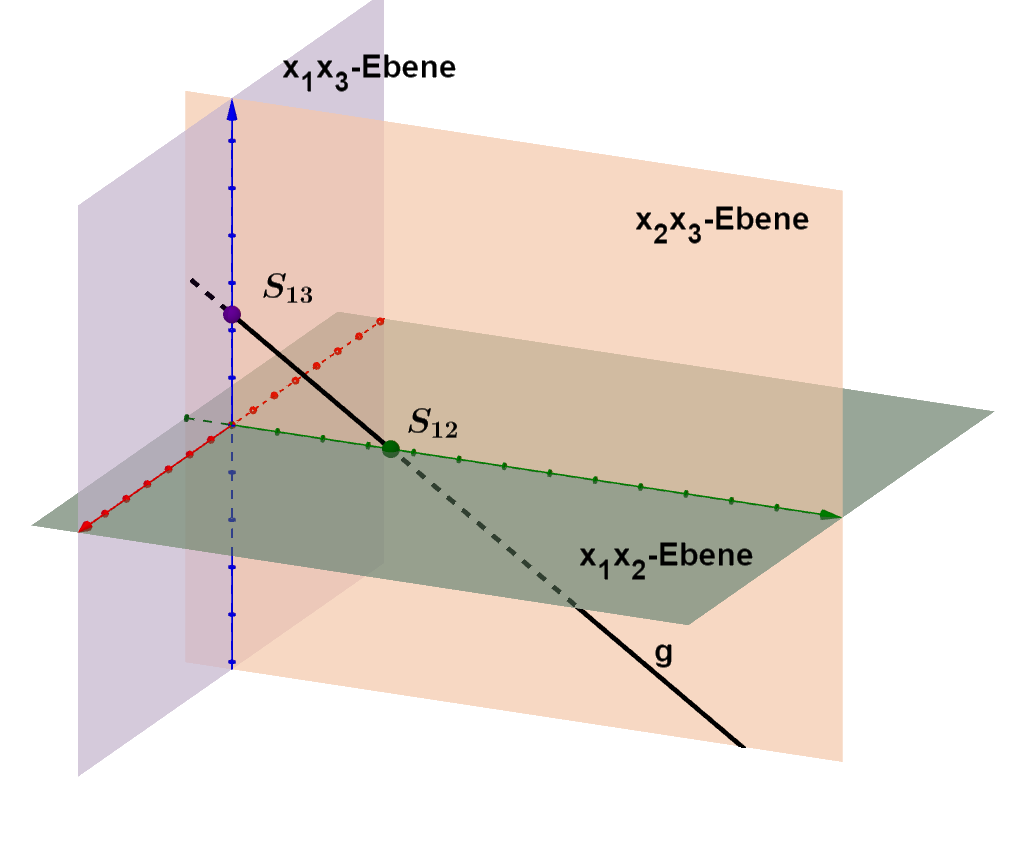
Lage der Geraden im Koordinatensystem
Die Gerade liegt in der -Ebene.
Hast du eine Frage oder Feedback?
- 2
Die Gerade hat nur einen einzigen Spurpunkt . Welche besondere Lage hat die Gerade im Koordinatensystem?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte von Geraden
Wegen liegt der einzige Spurpunkt in der -Ebene. Somit verläuft die Gerade parallel zur -Achse bzw. die Gerade ist parallel zur -Ebene und parallel zur -Ebene.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte von Geraden
Wegen liegt der einzige Spurpunkt in der -Ebene. Somit verläuft die Gerade parallel zur -Achse bzw. die Gerade ist parallel zur -Ebene und parallel zur -Ebene.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
