Ein spieltheoretisches Beispiel

Wenn wir die Feuerwehr rufen, entsteht ein kleiner Faktor, der uns unglücklich macht, dem teilen wir einen den Nutzen von $-5$ zu. Wenn wir nichts tun und geholfen wird, bleiben wir normal (Wert $0$). Wenn wir nichts tun und die Feuerwehr nicht kommt, sind wir furchtbar unglücklich, dem ordnen wir den Wert $-100$ zu. Weil wir Spieltheoretiker sind, vereinfachen wir, dass die Stärke der Gefühle (die Werte) für jede Person gleich stark ist und jede Person ausschließlich ihr eigenes Glück (Wert) maximieren will.

In einer Tabelle sähe das so aus:

Jetzt möchte jeder Spieler sein Glück maximieren. Wenn wir nur einen Spieler haben, ist es klar: Er ruft die Feuerwehr. Dann ist er bei $-5$, aber wenn er sie nicht gerufen hätte, kann nicht geholfen werden und er wird unglücklich (sein Nutzen ist $-100$).

Bei einem Spieler/Beobachter wird also immer die Feuerwehr gerufen.

Betrachten wir zunächst zwei Spieler

Bei zwei Spielern gibt es offensichtlich kein Gleichgewicht in reinen Strategien. Wenn beide die Feuerwehr rufen, hätte jeder lieber nicht die Feuerwehr gerufen, da die ja eh gekommen wäre. Wenn beide, nicht die Feuerwehr rufen, hätten wiederum beide gerne die Feuerwehr gerufen.

Es jedoch ein Gleichgewicht in gemischten Strategien, bei der jeder mit einer Wahrscheinlichkeit $p$ die Feuerwehr ruft.

Die Wahrscheinlichkeit $p$ von Spieler 1 muss so gewählt sein, dass es für Spieler 2 egal ist, welche Strategie er benutzt. In anderen Worten, der erwartete Nutzen beider Strategien ($u_2(\text{anrufen})$ und $u_2(\text{nicht anrufen})$) muss gleich sein.

Der erwartete Nutzen von $u_2(\text{anrufen})$ ist $-5$ ganz gleich was Spieler 1 macht. Der erwartete Nutzen von $u_2(\text{nicht anrufen})$ ist jedoch stark von dem abhängig, was Spieler 1 macht. Ruft er die Feuerwehr, haben wir einen Nutzen von $0$. Ruft er nicht die Feuerwehr, haben wir einen Nutzen von $-100$. Ruft er mit einer Wahrscheinlichkeit $p$ die Feuerwehr, haben wir einen Nutzen von:

$u_2(\text{nicht anrufen})=p\cdot0+(1-p)\cdot(-100)$

Für ein Gleichgewicht muss Spieler 1 und sein p so wählen, dass der erwartete Nutzen (von Spieler 2) unabhängig von der Strategie ist.

$u_2(\text{nicht anrufen})\overset{\underset{\mathrm{!}}{}}{=}u_2(\text{anrufen})$

$p\cdot 0+(1-p)\cdot (-100)=-5$

$(1-p)\cdot100=5$

$1-p=\frac{5}{100}$

$p=1-\frac{5}{100}=0{,}95$

Wenn beide Spieler mit einer Wahrscheinlichkeit von $p=0{,}95$ die Feuerwehr rufen, haben wir ein Gleichgewicht in gemischten Strategien.

Da jeder Teilnehmer mit einer Wahrscheinlichkeit von $(1-p)$ nicht die Feuerwehr ruft, ist die Wahrscheinlichkeit, dass keiner von beiden die Feuerwehr ruft, nicht mehr $0$, sondern

$(1-p)^2=2{,}5\cdot10^{-3}$

Was passiert wenn mehr Leute zuschauen?

Bei N gleichen Spielern, die alle in einem gemischten Gleichgewicht sind, muss es für jeden einzelnen Spieler egal sein, was er macht. Wenn der erwartete Nutzen einer reinen Strategie höher wäre, würde der Spieler die Strategie mit höherem erwarteten Nutzen spielen und von der gemischten Strategie abweichen.

Wie zuvor ist der erwartete Nutzen von $u_N(\text{anrufen})=-5$ unabhängig von dem, was die anderen Spieler machen. Der erwartete Nutzen von $u_N(\text{nicht anrufen})$  ist jedoch stark von dem abhängig was die anderen Spieler machen, ruft mindestens einer die Feuerwehr, haben wir einen Nutzen von $0,$ ruft niemand die Feuerwehr, einen Nutzen von $-100$.

Ein Beobachter ruft mit einer Wahrscheinlichkeit $p$ die Feuerwehr, also mit einer Wahrscheinlichkeit von $1-p$ nicht. Es gibt insgesamt $N-1$ andere Beobachter, alle die unabhängig voneinander agieren. Dementsprechend kann man die Wahrscheinlichkeit, dass die Feuerwehr nicht von den anderen nicht gerufen wird, mit $(1-p)^{N-1}$ berechnen.

Der Nutzen von „nicht anrufen“ ist also 0, wenn jemand anruft und mit einer Wahrscheinlichkeit von $(1-p)^{N-1}$ ist er $-100$. Der erwartete Nutzen ist daher:

$u_N(\text{nicht anrufen})=0+(1-p)^{N-1}\cdot(-100)$

Jetzt haben sich alle anderen Spieler ihr $p$ so gewählt, dass ein Gleichgewicht entsteht:

$u_N(\text{nicht anrufen})\overset{\underset{\mathrm{!}}{}}{=}u_N(\text{anrufen})$

$0+(1-p)^{N-1}\cdot(-100)=-5$

$(1-p)^{N-1}\cdot 100=5$

$(1-p)^{N-1}=\frac{5}{100}$

$1-p=(\frac{5}{100})^\frac{1}{N-1}$

$p=1-(\frac{5}{100})^\frac{1}{N-1}$

Jetzt ist es für den N-ten Spieler egal welche Strategie er wählt. Also wählt er wie alle die Strategie, mit einer Wahrscheinlichkeit von $p=1-(\frac{5}{100})^\frac{1}{N-1}$ die Feuerwehr zu rufen.

$p=1-(\frac{5}{100})^\frac{1}{N-1}$ ist vermutlich keine Funktion, die man sich so gut vorstellen kann, aber man kann sich versichern, dass die Funktion für größere N sinkt.

Hier ein Plot von der Wahrscheinlichkeit, dass ein Spieler von sich aus hilft ($y$-Achse) für unterschiedliche Spieler-Anzahlen $N$ ($x$-Achse)

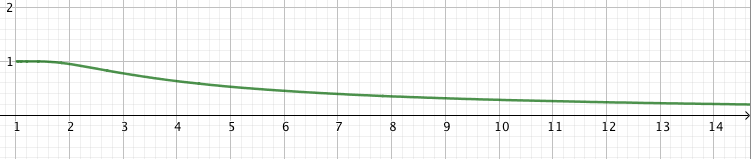
Dass es unwahrscheinlicher wird, dass ein spezieller Beobachter anruft, wenn mehrere Leute zuschauen, ist zu erwarten, da jetzt jeder Beobachter damit rechnet, dass ein anderer auch die Feuerwehr rufen könnte.

Ein interessantes Ergebnis erhalten wir, wenn wir ausrechnen, wie wahrscheinlich es ist, dass insgesamt die Feuerwehr kommt.

Ein Beobachter ruft mit einer Wahrscheinlichkeit $p$ die Feuerwehr, also mit einer Wahrscheinlichkeit von $1-p$ nicht. Es gibt insgesamt $N$ Beobachter, alle die unabhängig voneinander agieren.

Dementsprechend kann man die Wahrscheinlichkeit, dass die Feuerwehr nicht gerufen wird, mit $(1-p)^N$ berechnen.

$(1-p)^N= (1-(1-(\frac{5}{100})^\frac{1}{N-1}))^N$

$\hphantom{(1-p)^N}= (1-1+(\frac{5}{100})^\frac{1}{N-1})^N$

$\hphantom{(1-p)^N}= (\frac{5}{100}^\frac{1}{N-1})^N$

$\hphantom{(1-p)^N}= \frac{5}{100}^\frac{N}{N-1}$

Es wird also mit einer Wahrscheinlichkeit von $\frac{5}{100}^\frac{N}{N-1}$ nicht die Feuerwehr gerufen. Man kann sich überlegen, dass für größere N der Bruch in der Potenz etwa $1$ ist $(\frac{N}{N-1} \approx 1)$. Damit ist die Wahrscheinlichkeit, dass insgesamt nicht geholfen wird, etwa $(1-p)^N \approx \frac{5}{100}$

Interessanterweise ist die Wahrscheinlichkeit, dass die Feuerwehr kommt höher, wenn weniger Leute zusehen! Da die Funktion der Wahrscheinlichkeit das die Feuerwehr nicht kommt, stetig steigt.

Hier ein Plot von der Wahrscheinlichkeit, dass kein Spieler von sich aus hilft ($y$-Achse) für unterschiedliche Spieler-Anzahlen $N$ ($x$-Achse)

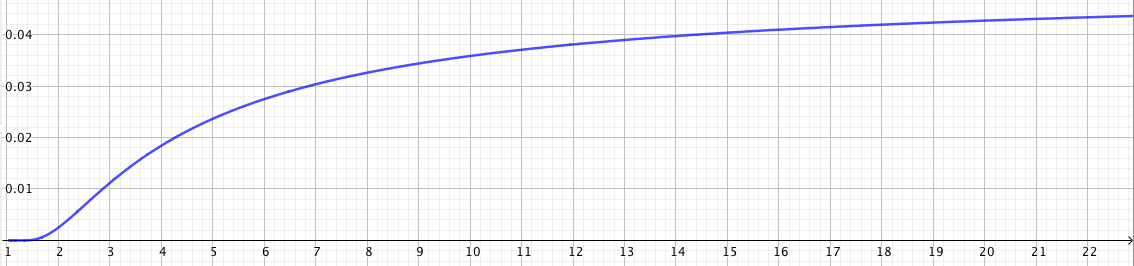
Aber aufgepasst, die Wahrscheinlichkeit, dass kein Spieler hilft, steigt zwar, aber sie wird nie $1$, sondern nähert sich wie gesagt $\frac{5}{100}$ an. Man kann also sagen, dass aus der Spieltheorie folgt, dass es unwahrscheinlicher ist, dass freiwillig geholfen wird, wenn mehrere Zuschauer beteiligt sind. Im Großteil der Fälle sollte jedoch geholfen werden.

Leider gibt es in der echten Welt immer wieder Beispiele, wo nicht geholfen wurde. Das wohl meist zitierte Beispiel hierfür ist vermutlich der Mord an Kitty Genovese. Der wurde von 38 Zeugen, die voneinander wussten, beobachtet. Aber keiner hat die Polizei gerufen.

Wenn ihr eine Situation sieht, die einen Freiwilligen verlangt (zum Beispiel, wenn ihr einen Rechtschreibfehler auf Serlo findet) gebt euch einen Ruck und leistet Hilfe! Wenn viele Leute Hilfe leisten könnten, heißt das noch nicht, dass es jemand tut.

Ausblick kooperative Spieltheorie

Der erwartete Gewinn von dem Gleichgewicht ist mit $-5$ nicht besonders hoch. Wenn man sich abspricht, hat man leicht bessere, mittlere Gewinne.

Wenn die Spieler sich absprechen würden, wäre es das beste (es würde den gesamten Nutzen maximieren), wenn ein einziger Spieler in den sauren Apfel beißt und anruft. Dann wird sicher geholfen und es kann nicht passieren, dass aus Versehen mehrere anrufen.

Die beste Strategie in der kooperativen Spieltheorie wäre es, dass nach einer Regel immer ein Spieler ausgewählt wird, der anruft. (zum Beispiel der älteste Beobachter)

Wenn man so eine Regel eingeführt hat, ist die Strategie halbwegs stabil. Der Älteste kann nicht nicht anrufen, da sonst keiner anruft und er leiden würde. Die Jungen wissen, dass sie nicht anrufen müssen und werden auch nicht anfangen anzurufen.

Diese Strategie hat jedoch zwei Probleme:

Zum einen ist es unfair, da immer derselbe (oder eine kleine Teilgruppe) anrufen muss.

Zum anderen ist es oft nicht sofort klar, wer von der Regel ausgewählt ist.

Wenn du zum Beispiel mit unbekannten Gleichaltrigen unterwegs bist und Feuer sieht, müsstet ihr erst mal klären, wer der älteste ist.

Suchen wir also eine faire Strategie, bei der jeder Spieler mit einer Wahrscheinlichkeit $p$ unabhängig voneinander die Feuerwehr ruft.

Wenn wir uns überlegen, was der Nutzen eines Spielers ist, wenn man mit einer Wahrscheinlichkeit p die Feuerwehr ruft. Erhalten wir folgende Funktion.

$v_N(p)=p\cdot u_N(\text{anrufen})+(1-p)\cdot u_N(\text{nicht anrufen})$

Wenn wir anrufen, haben wir einen Nutzen von $u_N(\text{anrufen})=-5$. Wenn wir nicht anrufen hängt es davon ab, ob jemand anderes anruft. Wie zuvor etabliert lässt sich das wie folgt ausrechnen.

$u_N(\text{nicht anrufen})=0+(1-p)^{N-1}\cdot(-100)$

$v_N(p)=p\cdot(-5)+(1-p)(0+(1-p)^{N-1}\cdot(-100))\newline v_N(p)=-5p-100\cdot(1-p)^{N}$

Wir wollen uns jetzt mit allen Spielern absprechen und das beste $p$ wählen, um am meisten Nutzen zu haben. Um das beste $p$ zu bestimmen, können wir das Maximum der Funktion $v(p)$ über das Ableiten der Funktion finden.

$v_N(p)=-5p-100\cdot(1-p)^{N} \newline v_N'(p)=-5-100\cdot N\cdot (1-p)^{N-1}\cdot(-1)$

Jetzt bestimmen wir die Nullstelle der Ableitung:

$\displaystyle -5+100\cdot N\cdot (1-p)^{N-1} =0 \newline 5=100\cdot N\cdot (1-p)^{N-1} \newline \frac{5}{100 \cdot N}= (1-p)^{N-1} \newline (\frac{5}{100 \cdot N})^{\frac{1}{N-1}}=1-p \newline p=1-(\frac{5}{100 \cdot N})^{\frac{1}{N-1}}$

Unsere beste abgesprochene Strategie ist also, dass jeder mit einer Wahrscheinlichkeit von $p=1-(\frac{5}{100 \cdot N})^{\frac{1}{N-1}}$ die Feuerwehr ruft. Damit ist unser erwarteter Nutzen gegeben als:

$v_N(p)=-5p-100\cdot(1-p)^{N}$

$\hphantom{v_N(p)}=-5(1-(\frac{5}{100 \cdot N})^{\frac{1}{N-1}} )-100\cdot(1-(1-(\frac{5}{100 \cdot N})^{\frac{1}{N-1}}) )^{N}$

$\hphantom{v_N(p)}=-5+5\cdot(\frac{5}{100 \cdot N})^{\frac{1}{N-1}} -100\cdot(\frac{5}{100 \cdot N})^{\frac{N}{N-1}}$

Hier ein Plot von dem erwartete Nutzen ($y$-Achse) der kooperativen Strategie für unterschiedliche Spieler-Anzahlen $N$ ($x$-Achse).

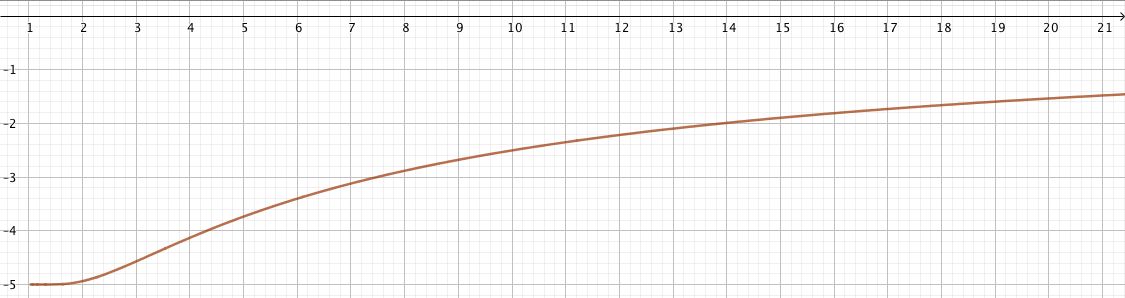
Man sieht, dass $v_N(p)\geq -5$ und somit ist der erwartete Nutzen besser als der des Gemischten-Gleichgewichtes. Zudem sieht man im Plot, dass der erwartete Nutzen für mehr Spieler steigt.

Dass der Nutzen steigt, liegt im Wesentlichen an zwei Punkten. Zum einen muss man seltener anrufen, wenn mehr Spieler mitspielen, zum andern wird in der kooperativen Strategie für größere Spielerzahlen öfter geholfen.

Bestimmen wir die Wahrscheinlichkeit, dass nicht geholfen wird.

$\displaystyle(1-p)^N=(1-(1-(\frac{5}{100\cdot N})^\frac{1}{N-1}))^N \\[2ex] \hphantom{(1-p)^N}=(1-1+(\frac{5}{100\cdot N})^\frac{1}{N-1})^N \\[2ex] \hphantom{(1-p)^N}=((\frac{5}{100\cdot N})^\frac{1}{N-1})^N \\[2ex] \hphantom{(1-p)^N}=(\frac{5}{100\cdot N})^{\frac{1}{N-1}\cdot N} \\[2ex] \hphantom{(1-p)^N}=(\frac{5}{100\cdot N})^{\frac{N}{N-1}}$

Man kann sich überlegen, dass für größere $N$ der Bruch in der Potenz etwa $1$ ist $(\frac{N}{N-1} \approx 1)$. Damit nimmt die Wahrscheinlichkeit, dass insgesamt nicht geholfen wird, in Abhängigkeit mit der Anzahl der Zuschauer ab: $(1-p)^N \approx \frac{5}{100\cdot N}$

Somit haben wir eine Strategie gefunden, die für alle Beteiligten ein besseren erwarteten Nutzen hat als das gemischte Gleichgewicht. Leider ist diese Strategie aber kein Gleichgewicht. Ein einzelner Spieler weiß, dass mit großer Wahrscheinlichkeit geholfen wird. Wenn er das weiß, ist für ihn eindeutig das beste, nicht anzurufen und von der gemeinschaftlichen Strategie abzuweichen.

Bitte weicht im echten Leben nicht von der gemeinschaftlichen Strategie ab und leistet ab und zu Hilfe, dann ist der erwartete Nutzen für alle besser.