Die Sektoren des abgebildeten Glücksrads sind gleich groß und mit den Zahlen von bis durchnummeriert.
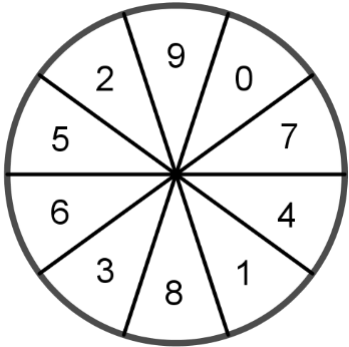
Das Glücksrad wird zwanzigmal gedreht. Bestimmen Sie die Wahrscheinlichkeit der Ereignisse A und B.
A: "Es wird genau siebenmal eine ungerade Zahl erzielt".
B: "Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt". (3 P)
