Graph

Viele Probleme kannst du mithilfe von Graphen modellieren.

Wenn du ein Problem geeignet als Graph modelliert hast, kannst du die Standard-Algorithmen der Graphentheorie darauf anwenden und so die Lösung des Problems berechnen.

Ein Beispiel: Du modellierst das Straßennetz deiner Heimatstadt als einen Graphen. Dann brauchst du nur noch den Kürzeste-Wege-Algorithmus anzuwenden, wenn du von A nach B navigieren willst.

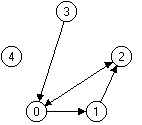
Ein Graph ist anschaulich dargestellt so etwas:

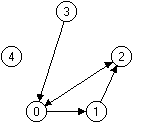
Formal gesehen besteht ein Graph aus einer endlichen, nichtleeren Menge $V$ von Knoten (die Kringel in der Darstellung) und einer Menge $E$ von Kanten (die Pfeile in der Darstellung).

Eine Kante ist eindeutig angegeben durch ihren Startknoten und ihren Endknoten. Damit lässt sich die Kante als Paar $(u, v)$ von zwei Knoten $u$ (dem Startknoten) und $v$ (dem Endknoten) angeben.

Der Graph aus der Abbildung besteht also aus der Knotenmenge $V = \{0{,}1,2{,}3,4\}$ und der Kantenmenge $E = \{ (0{,}1), (0{,}2), (1{,}2), (2{,}0), (3{,}0)\}$ .

Formal gesehen ist ein Graph ein Paar $G = (V, E)$ , wobei $V$ eine endliche, nichtleere Menge von Knoten und $E ~\subseteq~ V\times V$ die Menge der Kanten ist. Die Kanten sind Paare von je zwei Knoten; die Menge der Kanten $E$ ist also eine Teilmenge des kartesischen Produkts $V \times V$ und damit eine Relation auf der Menge $V$ .

Diese Relation kannst du in Worten etwa mit "ist durch eine dorthin gerichtete Kante verbunden mit" ausdrücken.

Pfad, Weg

Wenn du in einem Graphen von einem Knoten $u$ entlang der Kanten zu einem Knoten $v$ gelangst, beschreitest du einen Pfad (oder Kantenzug). Achte darauf, dass du dabei die Kanten in Pfeilrichtung durchläufst.

Definition

Ein Pfad ist eine endliche Folge von Kanten $(u_0, v_0) ... (u_{n-1},v_{n-1})$ , wobei jeweils $v_{i-1} = u_i ~ ~ (i = 1~ ... ~n-1)$ gilt. Die Kanten eines Pfades hängen also zusammen. Endknoten einer Kante ist jeweils Startknoten der folgenden Kante.

Die Anzahl $n$ der Kanten eines Pfades ist die Länge des Pfades.

Zum Beispiel ist $p_0 = (3{,}0)(0{,}1)(1{,}2)(2{,}0)(0{,}1)$ ein Pfad der Länge 5 in dem oben gezeigten Graphen.

Definition

Ein Pfad heißt einfacher Pfad, wenn er keine Kante mehrfach durchläuft. Der Pfad $p_{0}$ ist kein einfacher Pfad, denn er durchläuft die Kante (0,1) mehrfach. Wenn du die letzte Kante von $p_{0}$ weglässt, erhältst du einen einfachen Pfad $p_{1}$ .

Ein Pfad heißt Weg, wenn er keinen Knoten mehrfach durchläuft. Dies ist erfüllt, wenn alle $u_{i}$ untereinander und alle $v_{j}$ untereinander verschieden sind. Der Pfad $p_{1}$ ist zwar ein einfacher Pfad, aber kein Weg. Denn die Knoten $v_{j}$ sind nicht alle untereinander verschieden, der Knoten 0 tritt zweimal auf. Wenn du die letzte Kante von $p_{1}$ weglässt, erhältst du einen Weg $p_{2}$ .

Ein Pfad heißt Zyklus, wenn er geschlossen ist, wenn also sein Start- und Endknoten übereinstimmen.

Ein Zyklus, der ein Weg ist, heißt Kreis. Zum Beispiel ist der Pfad $p_3 = (1{,}2)(2{,}0)(0{,}1)$ ein Kreis. Denn Start- und Endknoten stimmen überein, und alle $u_{i}$ und alle $v_{j}$ sind untereinander verschieden.

Baum

In der Informatik spielen Bäume eine herausragende Rolle. Denn viele Daten lassen sich als hierarchische Struktur modellieren, also als eine Struktur, die sich von einem Punkt aus verzweigt. Eine solche Struktur wird als Baum bezeichnet.

Definition

Ein (gerichteter) Graph ist ein Baum, wenn

er genau einen Knoten enthält, zu dem keine Kante hinführt,
zu jedem anderen Knoten genau eine Kante hinführt und
er keinen Kreis enthält.

Der folgende gerichtete Graph ist ein Baum. Ein (gerichteter) Baum wird meist so gezeichnet, dass die Kanten von oben nach unten gerichtet sind.

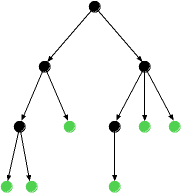
Ganz oben siehst du den Knoten, zu dem keine Kante hinführt; dieser Knoten ist die Wurzel des Baums. Zu jedem anderen Knoten führt genau eine Kante hin. Und außerdem enthält der Graph keinen Kreis. Er ist somit ein Baum.

Ferner erkennst du in dem Baum einige Knoten, von denen keine Kante wegführt; diese Knoten sind die Blätter des Baums (hier grün, wie Blätter nun einmal normalerweise sind, dargestellt). Alle anderen Knoten des Baums heißen innere Knoten.

Definition

In einem Baum wird die Länge des Weges von der Wurzel zu einem Knoten $v$ als die Tiefe des Knotens $v$ bezeichnet. Die Wurzel selbst hat somit die Tiefe 0.

Die Knoten gleicher Tiefe bilden eine Schicht im Baum.

Die Tiefe des gesamten Baums ist das Maximum der Tiefen aller seiner Knoten.

Beispielsweise hat der oben gezeigte Baum die Tiefe 3.

Binäre Bäume

Definition

Ein (gerichteter) Baum ist ein binärer Baum, wenn von jedem Knoten höchstens zwei Kanten wegführen.

Ein binärer Baum heißt vollständig, wenn von allen inneren Knoten genau zwei Kanten wegführen und wenn alle Blätter die gleiche Tiefe haben.

In der folgenden Abbildung siehst du einen vollständigen binären Baum der Tiefe 3:

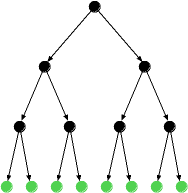
Manchmal ist auch die letzte Schicht in einem vollständigen binären Baum "angeknabbert" - es fehlen dort ein paar Knoten. Dann sprechen wir von einem fast vollständigen binären Baum. Die folgende Abbildung zeigt einen fast vollständigen binären Baum.

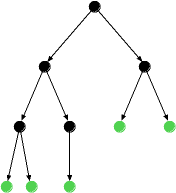
Bei (fast) vollständigen binären Bäumen stehen die Anzahl der Knoten und die Tiefe in engem Zusammenhang (siehe Übungsaufgabe).

Fast vollständige binäre Bäume spielen beispielsweise beim Sortierverfahren Heapsort eine Rolle.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?