Nachtermin Teil A - lernen mit Serlo!

Gegeben sind Sechsecke $AB_nC_nDE_nF_n$ mit der Symmetrieachse $AD$ . Der Punkt $G$ ist der Mittelpunkt der Strecken $[C_nE_n]$ und $[B_nF_n]$ .

Es gilt: $\overline{AG}=4\;\text{cm}$ und $\overline{DG}=3\;\text{cm}$ .

Die Winkel $B_nAF_n$ haben das Maß $\varphi$ und die Winkel $E_nDC_n$ haben das Maß $2\varphi$ mit $\varphi\in\,]0^\circ;\;90^\circ\lbrack.$

Die Zeichnung zeigt das Sechseck $AB_1C_1DE_1F_1$ für $\varphi= 40^\circ$ .

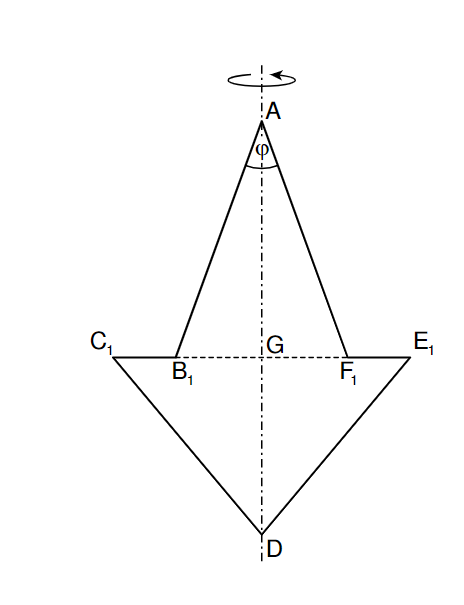
Zeigen Sie, dass für die Längen der Strecken $[B_nF_n]$ und $[C_nE_n]$ in Abhängigkeit von $\varphi$ gilt: $\overline{B_nF_n}(\varphi)=8\cdot \textrm{tan}(0{,}5\cdot\varphi)\,\textrm{cm}$ und $\overline{C_nE_n}(\varphi)=6\cdot \textrm{tan}\varphi \ \textrm{cm}.$

Die Längen der Strecken $\overline{B_nF_n}$ und $\overline{C_nE_n}$ :
Da $G$ der Mittelpunkt der Längen $\left[C_nE_n\right]$ und $\left[B_nF_n\right]$ ist, ist die gesuchte Länge $\overline{B_nF_n}=2\cdot\overline{B_nG}$ .
$\left[B_nG\right]$ im rechtwinkligen Dreieck $AB_nG$ (rot) mithilfe der Trigonometrie:
$\tan\left(\measuredangle GAB_n\right)=\frac{\textrm{Gegenkathete}}{\textrm{Ankathete}}$
$\tan\left(\measuredangle GAB_n\right)=\frac{\overline{B_nG}}{\overline{AG}}$
$\tan\left(0{,}5\cdot\varphi\right)=\frac{\overline{B_nG}}{4\;\text{cm}}$ | $\cdot\ 4\;\textrm{cm}$
$\overline{B_nG}=\tan\left(0{,}5\cdot\varphi\right)\cdot4\;\textrm{cm}$
Daraus folgt:
$\overline{B_nF_n}(\varphi)=2\cdot\overline{B_nG}=2\cdot\tan\left(0{,}5\cdot\varphi\right)\cdot4\;\textrm{cm} =8\cdot\tan\left(0{,}5\cdot\varphi\right)\;\textrm{cm}$
Da G der Mittelpunkt der Längen $\left[C_nE_n\right]$ und $\left[B_nF_n\right]$ ist, ist die gesuchte Länge $\overline{C_nE_n}=2\cdot\overline{C_nG}$ .
Wir gehen wie oben vor:
$\left[C_nG\right]$ im rechtwinkligen Dreieck $C_nDG$ (rot) mithilfe der Trigonometrie:
$\tan\left(\measuredangle GDC_n\right)=\frac{\textrm{Gegenkathete}}{\textrm{Ankathete}}$
$\tan\left(\measuredangle GDC_n\right)=\frac{\overline{C_nG}}{\overline{DG}_{ }}$
$\tan\left(\varphi\right)=\frac{\overline{C_nG}}{3\;\textrm{cm}}$ | $\cdot\ 3\;\textrm{cm}$
$\overline{C_nG}=\tan\left(\varphi\right)\cdot3\;\textrm{cm}$
$\overline{C_nE_n}(\varphi)=2\cdot\overline{C_nG}=2\cdot\tan\left(\varphi\right)\cdot3\;\textrm{cm}=6\cdot\tan\varphi\;\textrm{cm}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Die Sechsecke $AB_nC_nDE_nF_n$ rotieren um die Gerade $AD$ .

Zeigen Sie, dass für den Oberflächeninhalt $O$ der entstehenden Rotationskörper in Abhängigkeit von $\varphi$ gilt:

$O(\varphi)=\bigg(16\pi\cdot \frac{{\tan(0{,}5\cdot\varphi})}{\cos(0{,}5\cdot\varphi)}+9 \pi\cdot\frac{{\tan(\varphi})}{\cos(\varphi)}+9\pi\cdot \tan^2\varphi-16\pi\cdot \tan^2(0{,}5\cdot\varphi)\bigg)\ \text{cm}^2$

Oberflächeninhalt von dem entstehenden Rotationskörper:

Der Rotationskörper setzt sich aus zwei Kegeln zusammen, daher können wir die Oberfläche wie folgt berechnen:

$O_{Rotationskörper}=O_{Kegel\ 1}$ (grün) + $O_{Kegel\ 2}$ (blau) - $2\cdot K_1$ (Kreisfläche zwischen den Kegeln)

Allgemein: $O=r^2\cdot\pi+r\cdot\pi\cdot$ s

Wir kennen die Radien der beiden Kegel, benötigen aber bei beiden Kegeln noch die Seitenlänge s.

Seitenlänge $s_1=\overline{AB_n}$ : Im rechtwinkligen Dreieck $AB_nG$ (siehe oben) mit Hilfe der Trigonometrie:

$\cos\left(\measuredangle B_nGA\right)=\frac{\textrm{Gegenkathete}}{\textrm{Ankathete}}=\frac{\overline{AG}}{s_1}$

$s_1=\frac{\overline{AG}}{\cos\left(\measuredangle B_nGA\right)}=\frac{4\;\textrm{cm}}{\cos\left(0{,}5\cdot\varphi\right)}$

Seitenlänge $s_2=\overline{C_nD}$ : Im rechtwinkligen Dreieck $C_1DG$ (siehe oben) mit Hilfe der Trigonometrie:

$\cos\left(\measuredangle GDC_1\right)=\frac{\textrm{Gegenkathete}}{\textrm{Ankathete}}=\frac{\overline{DG}}{s_2}$

$s_2=\frac{\overline{DG}}{\cos\left(\measuredangle GDC_1\right)}=\frac{3\;\textrm{cm}}{\cos\varphi}$

Jetzt können wir die Seitenlängen in die Formel einsetzen:

$\displaystyle O_1\left(\varphi\right)$	$=$	$\displaystyle r_1^2\cdot\pi+r_1\cdot\pi\cdot s_1$
	$=$	$\displaystyle \left(\left(\tan\left(0{,}5\cdot\varphi\right)\cdot4\;\textrm{cm}\right)^2\cdot\pi+\left(\tan\left(0{,}5\cdot\varphi\right)\cdot\pi\cdot4\;\textrm{cm}\right)\cdot\frac{4\;\textrm{cm}}{\cos\left(0{,}5\cdot\varphi\right)}\right)$
	$=$	$\displaystyle \left(16\pi\cdot\tan^2\left(0{,}5\cdot\varphi\right)+16\pi\cdot\frac{\tan\left(0{,}5\cdot\varphi\right)}{\cos\left(0{,}5\cdot\varphi\right)}\right)\;\textrm{cm}^2$

$\displaystyle O_2\left(\varphi\right)$	$=$	$\displaystyle r_2^2\cdot\pi+r_2\cdot\pi\cdot s_2$
	$=$	$\displaystyle \left(r_2^2\cdot\pi+r_2\cdot\pi\cdot s_2\right)$
	$=$	$\displaystyle \left(\left(\tan\left(\varphi\right)\cdot3\;\textrm{cm}\right)^2\cdot\pi+\left(\tan\left(\varphi\right)\cdot3\;\textrm{cm}\right)\cdot\pi\cdot\frac{3\;\textrm{cm}}{\cos\varphi}\right)$
	$=$	$\displaystyle \left(9\pi\cdot\tan^2\varphi+9\pi\cdot\frac{\tan\varphi}{\cos\varphi}\right)\;\textrm{cm}^2$

$\displaystyle K_1\left(\varphi\right)$	$=$	$\displaystyle r_1^2\cdot\pi$
	$=$	$\displaystyle \left(\tan\left(0{,}5\cdot\varphi\right)\cdot4\;\textrm{cm}\right)^2\cdot\pi$
	$=$	$\displaystyle 16\pi\cdot\tan^2\left(0{,}5\cdot\varphi\right)$

$\displaystyle O\left(\varphi\right)$	$=$	$\displaystyle O_1+O_2-2\cdot K_1$
	$=$	$\displaystyle \left(16\pi\cdot\tan^2\left(0{,}5\cdot\varphi\right)+16\pi\cdot\frac{\tan\left(0{,}5\cdot\varphi\right)}{\cos\left(0{,}5\cdot\varphi\right)}+9\pi\cdot\tan^2\varphi+9\pi\cdot\frac{\tan\varphi}{\cos\varphi}-2\cdot\left(16\pi\cdot\tan^2\left(0{,}5\cdot\varphi\right)\right)\right)\;\textrm{cm}^2$
	↓	Sortieren wie in der Angabe.
	$=$	$\displaystyle \left(16\pi\cdot\frac{\tan\left(0{,}5\cdot\varphi\right)}{\cos\left(0{,}5\cdot\varphi\right)}+9\pi\cdot\frac{\tan\varphi}{\cos\varphi}+9\pi\cdot\tan^2\varphi+16\pi\cdot\tan^2\left(0{,}5\cdot\varphi\right)-32\pi\cdot\tan^2\left(0{,}5\cdot\varphi\right)\right)\;\textrm{cm}^2$
	$=$	$\displaystyle \left(16\pi\cdot\frac{\tan\left(0{,}5\cdot\varphi\right)}{\cos\left(0{,}5\cdot\varphi\right)}+9\pi\cdot\frac{\tan\varphi}{\cos\varphi}+9\pi\cdot\tan^2\varphi-16\pi\cdot\tan^2\left(0{,}5\cdot\varphi\right)\right)\;\textrm{cm}^2$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Für das Sechseck $AB_2C_2DE_2F_2$ gilt: $\overline{AB_2}=\overline{B_2F_2}=\overline{F_2A}$ .

Zeichnen Sie das Sechseck $AB_2C_2DE_2F_2$ in die Zeichnung zur Aufgabenstellung ein.

Berechnen Sie sodann den Oberflächeninhalt des zugehörigen Rotationskörpers. Runden Sie auf zwei Nachkommastellen.

Zeichnung des Sechsecks $AB_2C_2DE_2F_2$ :

Es gilt: $\overline{AB_2}=\overline{B_2F_2}=\overline{F_2A}$ , das Dreieck $AB_2F_2$ ist folglich gleichseitig und gleichwinklig: $\measuredangle F_2AB_2=\measuredangle AB_2F_2=\measuredangle B_2F_2A=60^\circ$ .

Ausführliche Zeichnung:

Wir wissen, dass $\varphi=60^\circ$ ist, folglich können wir an $A$ zwei $30^\circ$ -Winkel messen (blau und grün) und die beiden Halbgeraden zeichnen.
Die Halbgeraden schneiden die Seite $\left[C_nE_n\right]$ in den Punkten $B_2$ und $F_2$ (rot).

Oberflächeninhalt des Körpers für $\varphi=60^\circ$ :

$\displaystyle O\left(\varphi \right)$	$=$	$\displaystyle \left(16\pi\cdot\frac{\tan\left(0{,}5\cdot\varphi\right)}{\cos\left(0{,}5\cdot\varphi\right)}+9\pi\cdot\frac{\tan\varphi}{\cos\varphi}+9\pi\cdot\tan^2\varphi-16\pi\cdot\tan^2\left(0{,}5\cdot\varphi\right)\right)\;\textrm{cm}^2$
	↓	Setze $\varphi=60^\circ$ ein.
$\displaystyle O\left(60^{\circ }\right)$	$=$	$\displaystyle \left(16\pi\cdot\frac{\tan\left(0{,}5\cdot60^\circ\right)}{\cos\left(0{,}5\cdot60^\circ\right)}+9\pi\cdot\frac{\tan60^\circ}{\cos60^\circ}+9\pi\cdot\tan^2(60^\circ)-16\pi\cdot\tan^2\left(0{,}5\cdot60^\circ\right)\right)\;\textrm{cm}^2$
$\displaystyle O\left(60^{\circ }\right)$	$=$	$\displaystyle \left(16\pi\cdot\frac{\tan\left(30^\circ\right)}{\cos\left(30^\circ\right)}+9\pi\cdot\frac{\tan60^\circ}{\cos60^\circ}+9\pi\cdot\tan^2(60^\circ)-16\pi\cdot\tan^2\left(30^\circ\right)\right)\;\textrm{cm}^2$
$\displaystyle O\left(60^{\circ }\right)$	$=$	$\displaystyle \left(16\pi\cdot\frac{2}{3}+9\pi\cdot2\sqrt{3}+9\pi\cdot3-16\pi\cdot\frac{1}{3}\right)\;\textrm{cm}^2$
$\displaystyle O\left(60^{\circ }\right)$	$=$	$\displaystyle \left(\frac{32}{3}\pi+18\pi\sqrt{3}+27\pi-\frac{16}{3}\pi\right)\;\textrm{cm}^2$
	↓	Klammere $\pi$ aus.
$\displaystyle O\left(60^{\circ }\right)$	$=$	$\displaystyle \pi\left(\frac{32}{3}+18\sqrt{3}+27-\frac{16}{3}\right)\;\textrm{cm}^2$
	↓	Fasse zusammen.
$\displaystyle O\left(60^{\circ }\right)$	$=$	$\displaystyle 199{,}52\;\textrm{cm}^2$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇