Aufgabe 5
Claudia untersucht eine rote Kerze.
Die rote Kerze ist lang. In einer Stunde brennen ab.

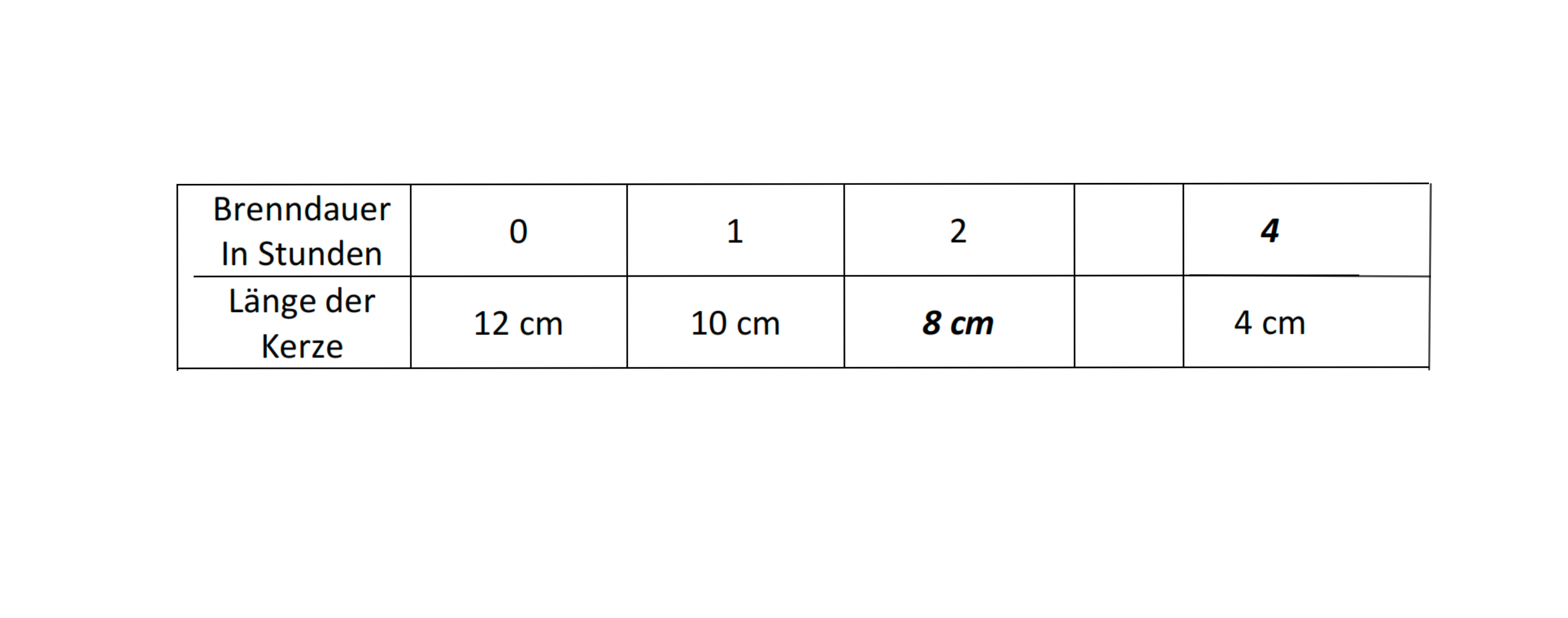
Vervollständige die Tabelle für die Brenndauer der roten Kerze. (2 BE)
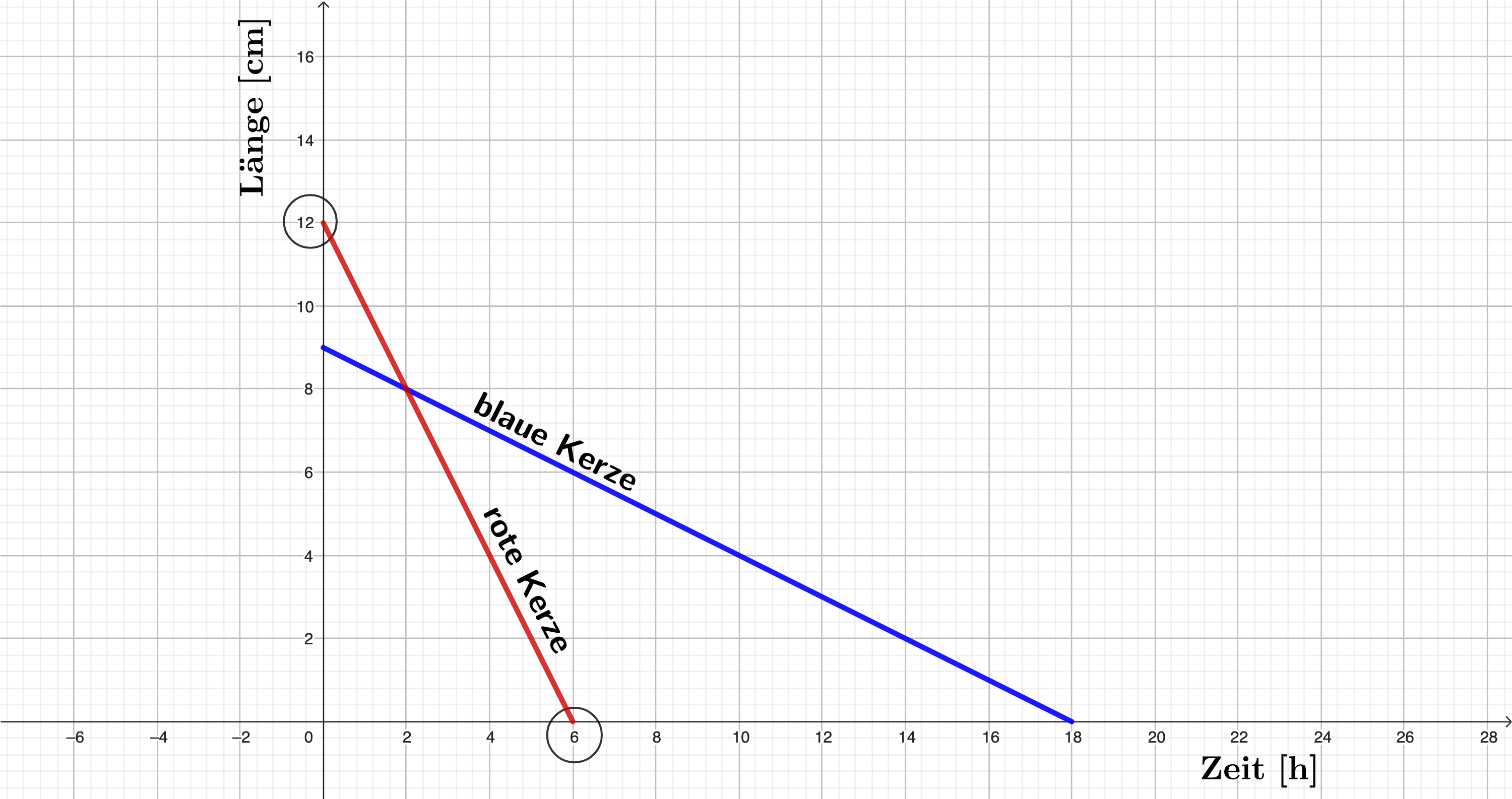
Zeichne den Graphen zur roten Kerze in das Koordinatensystem. (2 BE)
Claudia stellt zur roten Kerze die Funktionsgleichung auf.
Gib die Bedeutung der Zahl -2 im Sachzusammenhang an. (1 BE)
Berechne die Länge der roten Kerze nach 3,5 Stunden. (2 BE)
Claudia bläst die rote Kerze aus, wenn sie nur noch lang ist.
Bestimme, wann sie die Kerze ausbläst. (2 BE)
In dem Koordinatensystem siehst du den Graphen für eine blaue Kerze.
Entscheide, welche Kerze länger brennt, wenn die Kerzen nicht ausgeblasen werden.
Begründe deine Entscheidung. (2 BE)
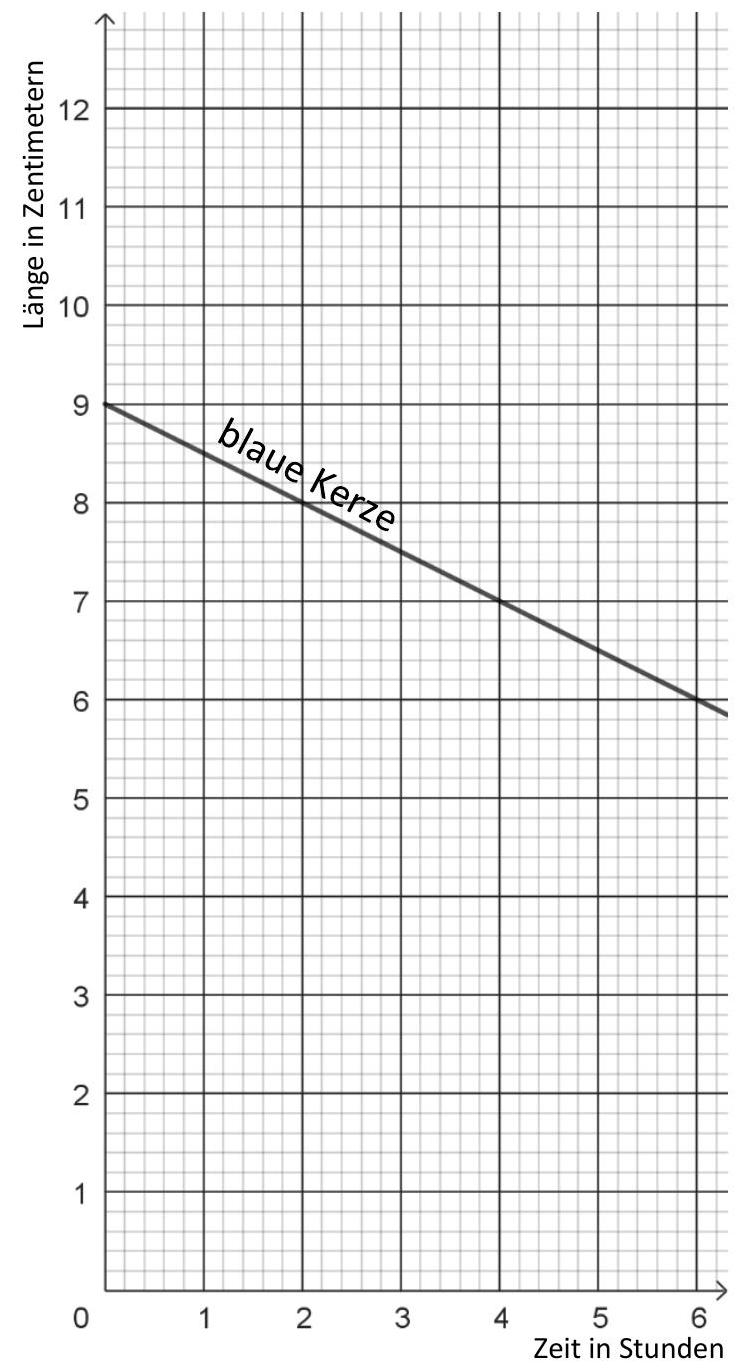
Kreuze an, welche Funktionsgleichung zur blauen Kerze passt.
Begründe, warum die anderen Funktionsgleichungen nicht passen. (3 BE)
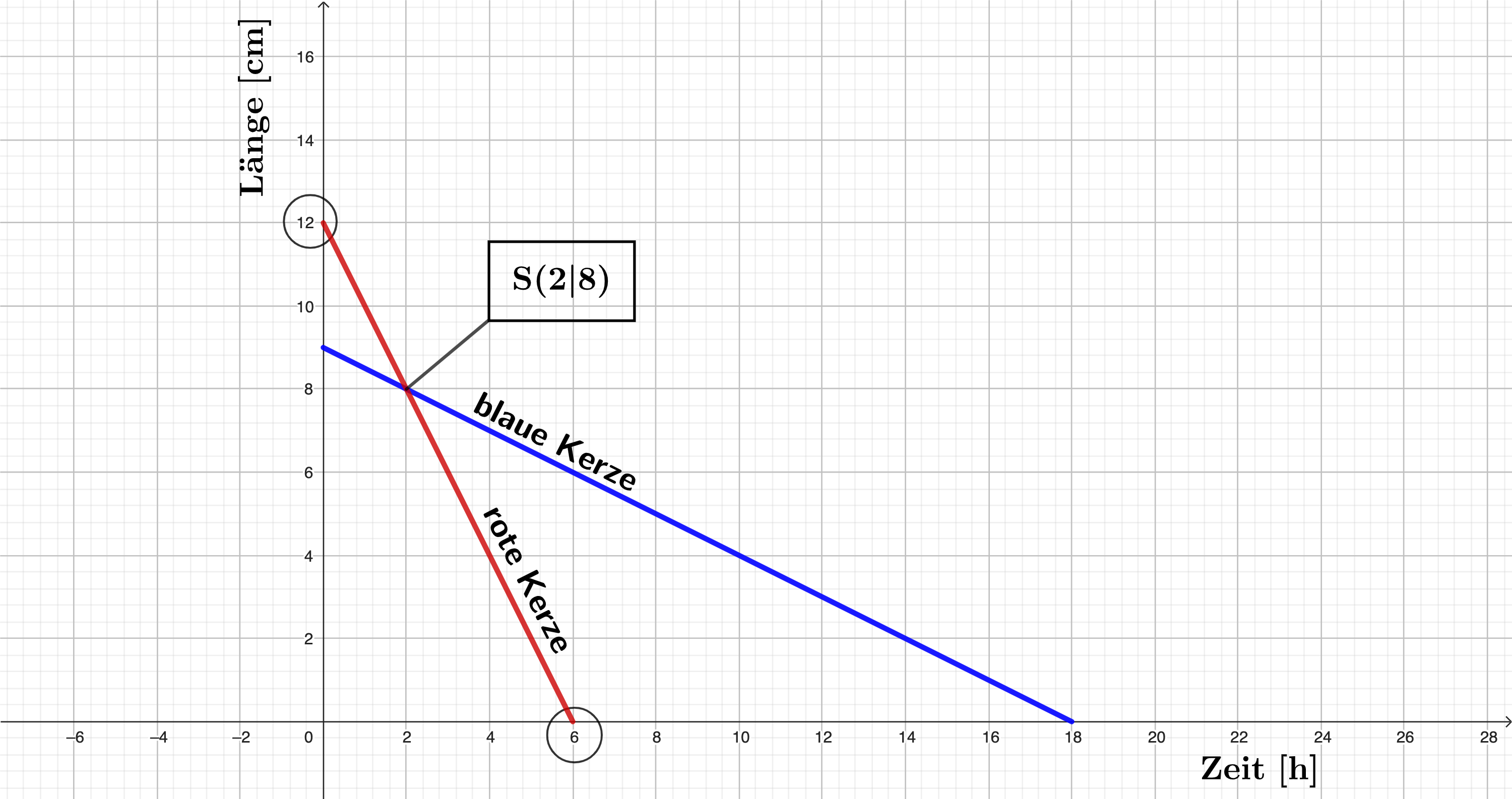
Gib den Schnittpunkt der beiden Graphen an.
Gib die Bedeutung des Schnittpunkts im Sachzusammenhang an. (3 BE)
Du siehst drei Kerzen.
Ordne jeder Kerze den passenden Graphen zu. Begründe deine Zuordnung. (3 BE)
Du kannst die Bilder anklicken und mit der Maus verschieben.
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen