Aufgabe 2B
Ein Unternehmen stellt Tischtennisbälle her. der hergestellten Bälle weichen nur unwesentlich von der Kugelform ab; diese werden im Weiteren als „rund“ bezeichnet, die übrigen als „unrund“. Aus der großen Menge der hergestellten Bälle werden regelmäßig Stichproben entnommen, wobei die Auswahl der Bälle für jede Stichprobe als zufällig angenommen werden kann. Die Zufallsgröße gibt die Anzahl der runden Bälle in diesen Stichproben an. ist binomialverteilt.
Es wird eine Stichprobe von Bällen untersucht.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Stichprobe
nur runde Bälle enthält,
mindestens runde Bälle enthält,
genau einen oder genau zwei unrunde Bälle enthält.
(4BE)
Nach der Herstellung durchlaufen die Bälle eine Sortieranlage. Dabei wird ein unrunder Ball mit einer Wahrscheinlichkeit von aussortiert. Allerdings werden auch der runden Bälle aussortiert.
Stellen Sie den Prozess der Herstellung und Sortierung der Bälle in einem beschrifteten Baumdiagramm dar. (3BE)
Beschreiben Sie die Bedeutung des Terms im Sachzusammenhang. (2BE)
Angenommen, die nicht aussortierten Bälle würden die gleiche Sortieranlage ein zweites Mal durchlaufen.
Begründen Sie, dass die Wahrscheinlichkeit dafür, dass ein nach zweimaligem Durchlaufen der Anlage zufällig ausgewählter Ball unrund ist und nicht aussortiert wird, ist.
Berechnen Sie den Anteil der unrunden Bälle unter denjenigen, die dann nach zweimaligem Durchlaufen der Anlage nicht aussortiert würden. (4BE)
Das Gewicht eines Tischtennisballs soll Gramm (g) betragen. Bei einer Kontrolle einer sehr großen Anzahl von Bällen der Produktion wurden die in der Tabelle aufgeführten relativen Häufigkeiten für die Gewichte der Bälle festgestellt.
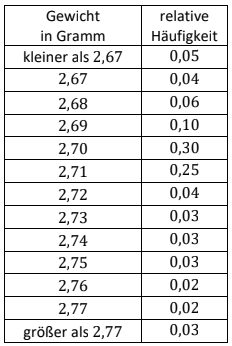
Begründen Sie, warum es nicht möglich ist, zu den in der Tabelle vorliegenden Daten das arithmetische Mittel der Gewichte zu berechnen. (2BE)
Die relativen Häufigkeiten aus der Tabelle werden im Folgenden als Wahrscheinlichkeiten verwendet.
Geben Sie das größte Gewicht an, das ein zufällig ausgewählter Ball mit einer Wahrscheinlichkeit von höchstens unterschreitet. (2BE)
Bestimmen Sie die Wahrscheinlichkeit dafür, dass in einer Stichprobe von zufällig ausgewählten Bällen höchstens einer ein Gewicht aufweist, das kleiner als g oder größer als g ist. (3BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

