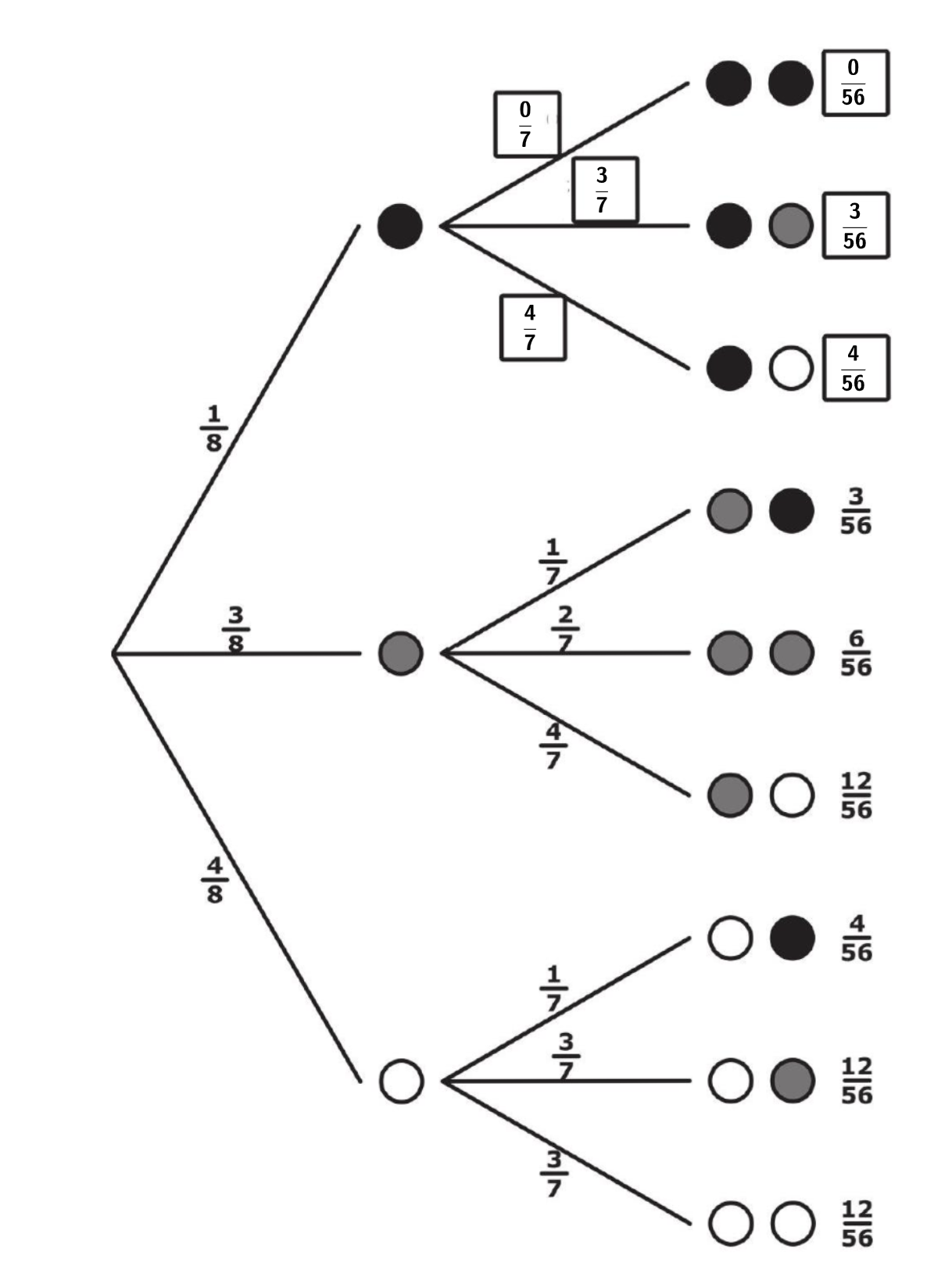
Bei einem Spiel sind eine schwarze, drei graue und vier weiße Kugeln in einer Schachtel. Es werden nacheinander zwei Kugeln gezogen. Dabei wird die zuerst gezogene Kugel nicht zurückgelegt.
Das Spiel ist gewonnen, wenn beide gezogenen Kugeln die gleiche Farbe haben.
Kieron hat das Baumdiagramm dazu fast vollständig gezeichnet:
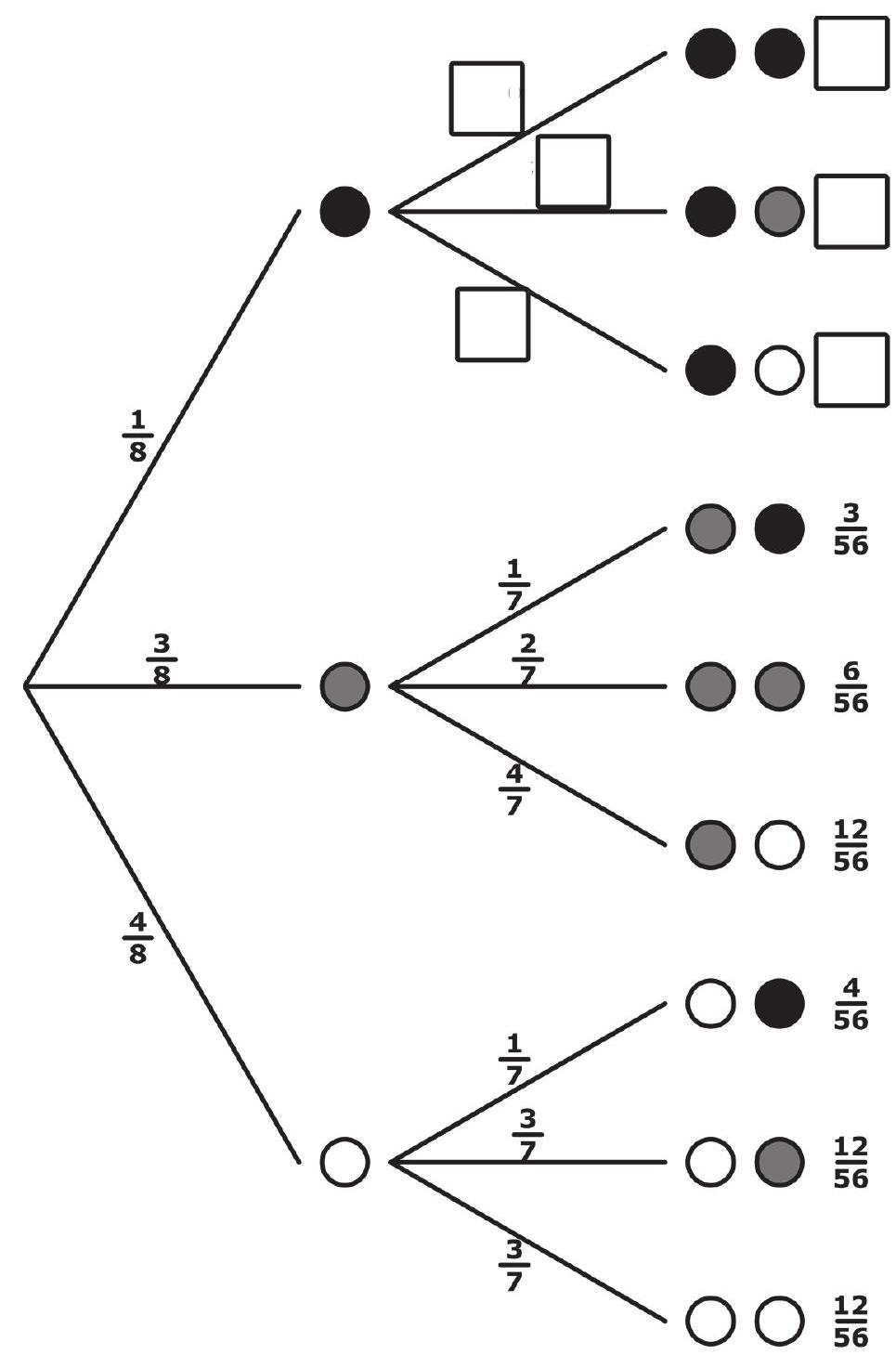
Petra bemängelt: „Das Baumdiagramm ist gar nicht fertig."
Ergänze die fehlenden Wahrscheinlichkeiten in den Kästchen. (2 Punkte)
Erläutere, warum die Nenner aller Brüche in der zweiten Stufe um eins niedriger sind als in der ersten Stufe. (1 Punkt)
Gib die Wahrscheinlichkeit dafür an, das Spiel zu gewinnen. (1 Punkt)
Es fällt auf, dass Wahrscheinlichkeiten für zwei Kugeln verschiedener Farben gleich sind, egal welche der beiden Farben zuerst gezogen wurde. (Zum Beispiel Grau-Weiß oder Weiß-Grau)
Begründe, dass das immer so ist - unabhängig von der Anzahl der Kugeln in der Schachtel. (2 Punkte)
Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt.