Heft 2 - B4

🎓 Prüfungsbereich für Schleswig-Holstein

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Bei einem Spiel sind eine schwarze, drei graue und vier weiße Kugeln in einer Schachtel. Es werden nacheinander zwei Kugeln gezogen. Dabei wird die zuerst gezogene Kugel nicht zurückgelegt.
Das Spiel ist gewonnen, wenn beide gezogenen Kugeln die gleiche Farbe haben.
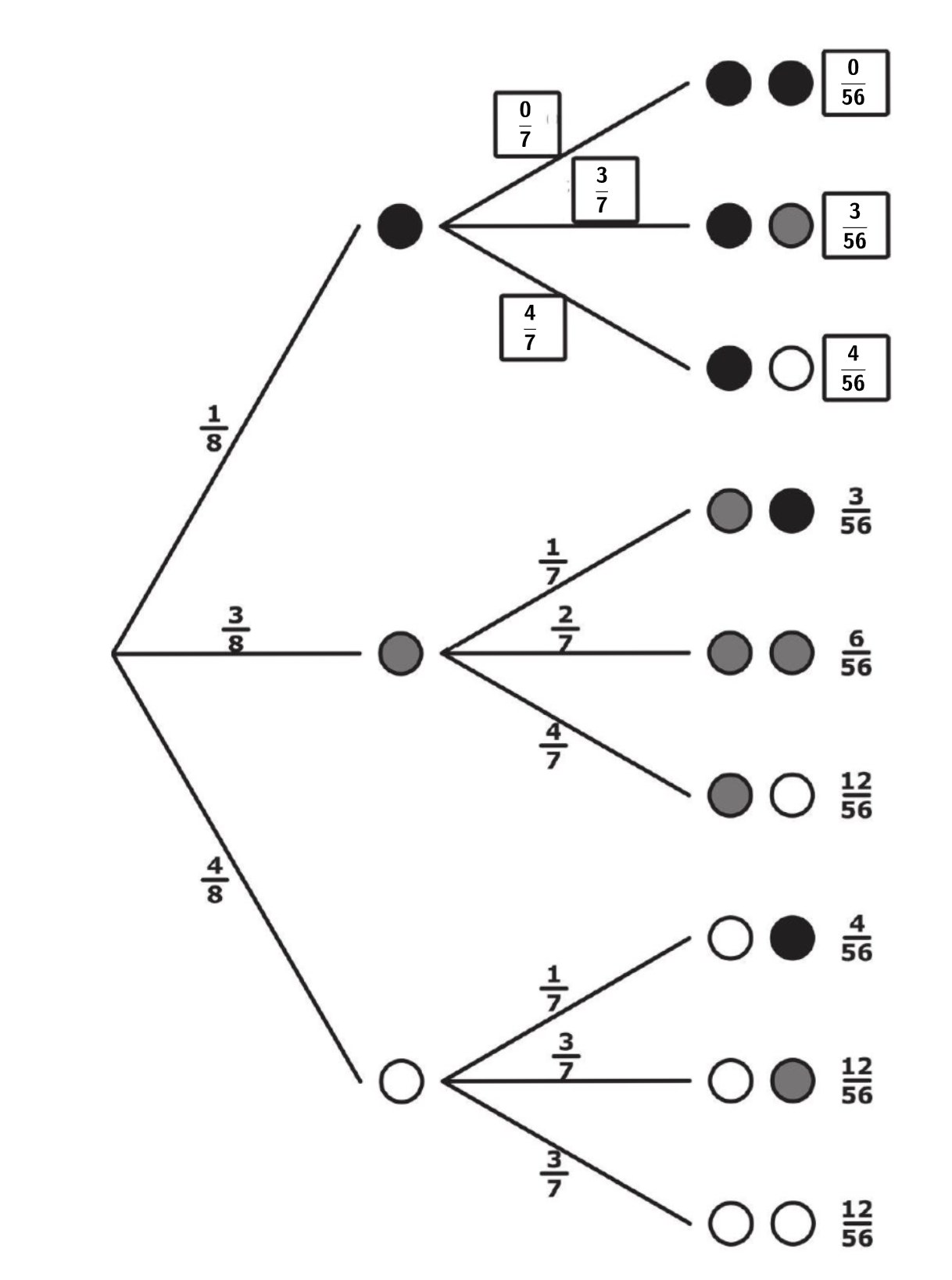
Kieron hat das Baumdiagramm dazu fast vollständig gezeichnet:
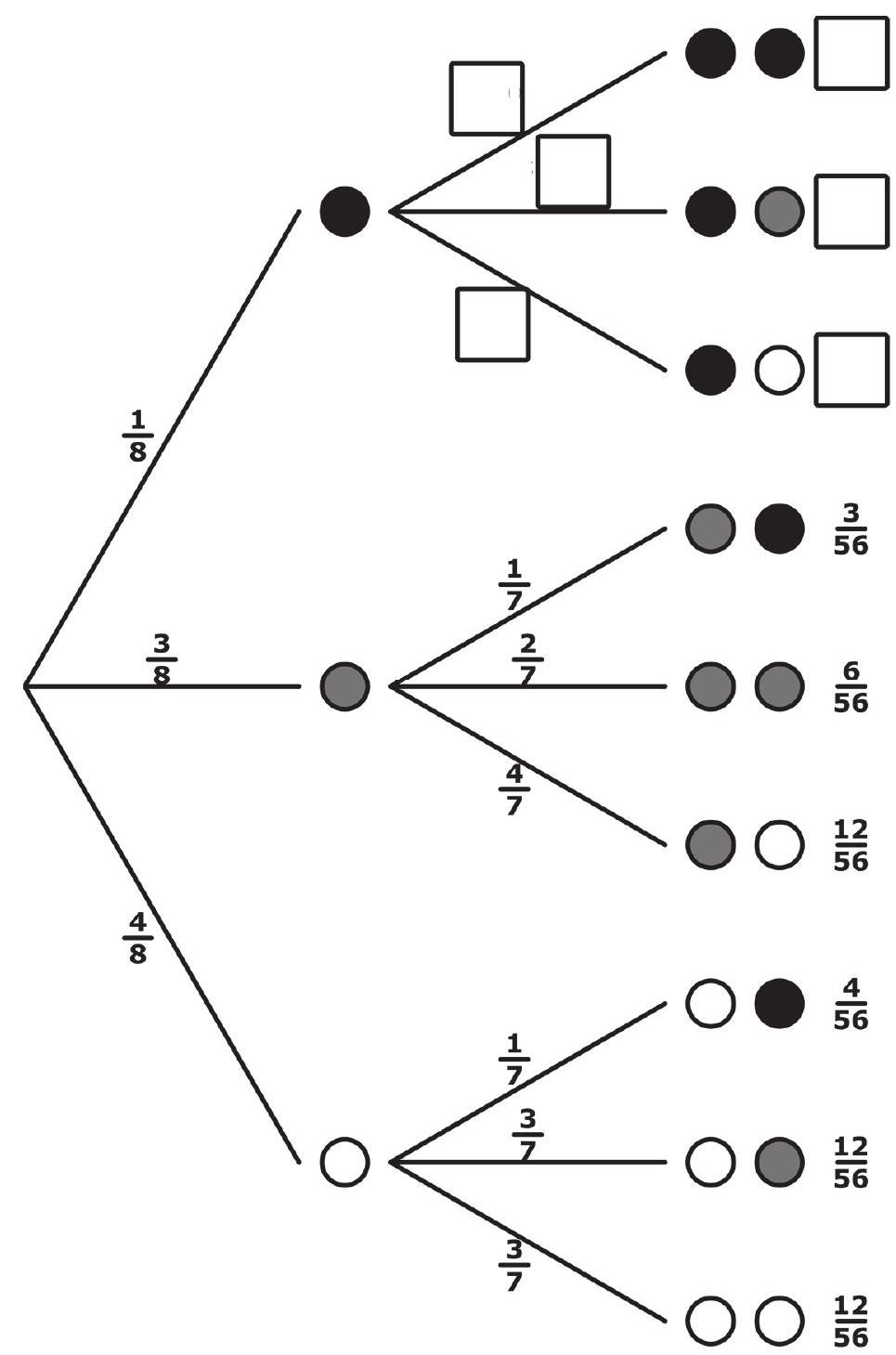
1. Petra bemängelt: „Das Baumdiagramm ist gar nicht fertig."
  Ergänze die fehlenden Wahrscheinlichkeiten in den Kästchen. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Ergänzen der fehlenden Wahrscheinlichkeiten in den Kästchen:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Achte darauf, dass hier ohne Zurücklegen gezogen wird.
  Zähle anhand der anderen Äste, wie viele Kugeln von den verschiedenen Farben vorhanden sind.
2. Erläutere, warum die Nenner aller Brüche in der zweiten Stufe um eins niedriger sind als in der ersten Stufe. (1 Punkt)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Erläuterung
  Da die Kugel nach dem ersten Ziehen nicht zurückgelegt wird, ist nach dem ersten Ziehen eine Kugel weniger in der Schachtel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte, die erste gezogene Kugel wird nicht zurückgelegt.
3. Gib die Wahrscheinlichkeit dafür an, das Spiel zu gewinnen. (1 Punkt)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Berechnen der Wahrscheinlichkeit zwei Kugeln gleicher Farbe zu ziehen:
  $\hspace{25mm}\mathrm{P_{weiß}=\dfrac{4}{8}\cdot\dfrac{3}{7}=\dfrac{12}{56}}\qquad\qquad\mathrm{P_{grau}=\dfrac{3}{8}\cdot\dfrac{2}{7}=\dfrac{6}{56}}$
  $\hspace{40mm}\mathrm{P_{gesamt}=\dfrac{12}{56}+\dfrac{6}{56}=\dfrac{18}{56}}$
  Die Wahrscheinlichkeit das Spiel zu gewinnen beträgt, $\ \boxed{\dfrac{18}{56}}$ .
  Schreibe den Wert in die Lücke.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte, es ist nur eine schwarze Kugel in der Schachtel. Überlege, wie groß die Wahrscheinlichkeit ist, zwei weiße oder zwei graue Kugeln zu ziehen. Nimm das Baumdiagramm zu Hilfe.
4. Es fällt auf, dass Wahrscheinlichkeiten für zwei Kugeln verschiedener Farben gleich sind, egal welche der beiden Farben zuerst gezogen wurde. (Zum Beispiel Grau-Weiß oder Weiß-Grau)
  Begründe, dass das immer so ist - unabhängig von der Anzahl der Kugeln in der Schachtel. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Begründung, dass Wahrscheinlichkeiten für zwei Kugeln verschiedener Farben gleich sind:
  Die Wahrscheinlichkeit setzt sich zusammen aus den Brüchen:
  $P_\text{grau-weiß}=\dfrac38\cdot \dfrac47$
  oder auch
  $P_\text{weiß-grau}=\dfrac48\cdot \dfrac37$
  Die Zähler werden beim Berechnen des Produkts einfach multipliziert. Bei einer Multiplikation kann man die Faktoren vertauschen, weshalb die Reihenfolge nicht wichtig ist:
  $P_\text{grau-weiß}=\dfrac38\cdot \dfrac47=\dfrac{3\overset{\curvearrowright}{\cdot} 4}{8\cdot 7}=\dfrac48\cdot \dfrac37=P_\text{weiß-grau}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
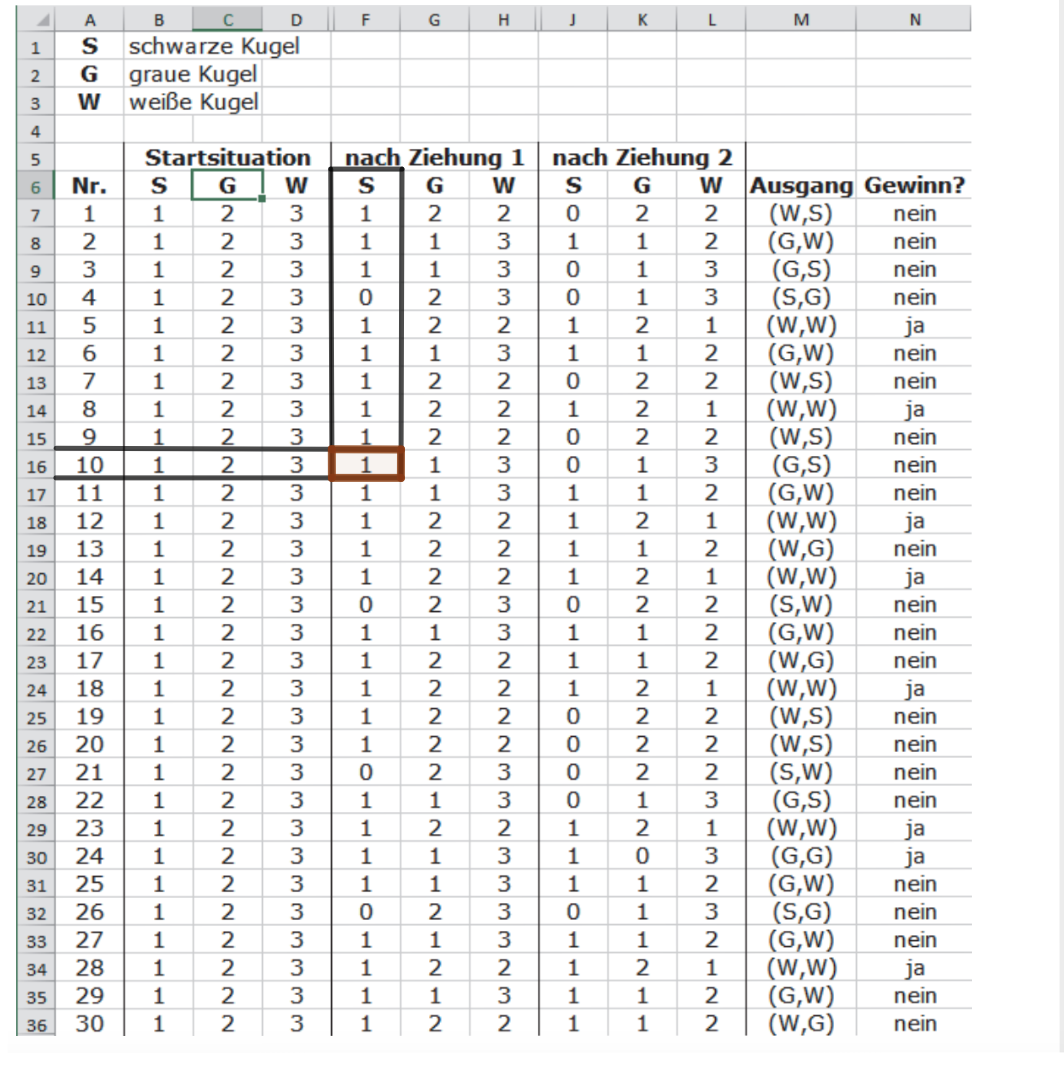
Bei einem anderen Spiel wurde mit Hilfe einer Tabellenkalkulation simuliert.
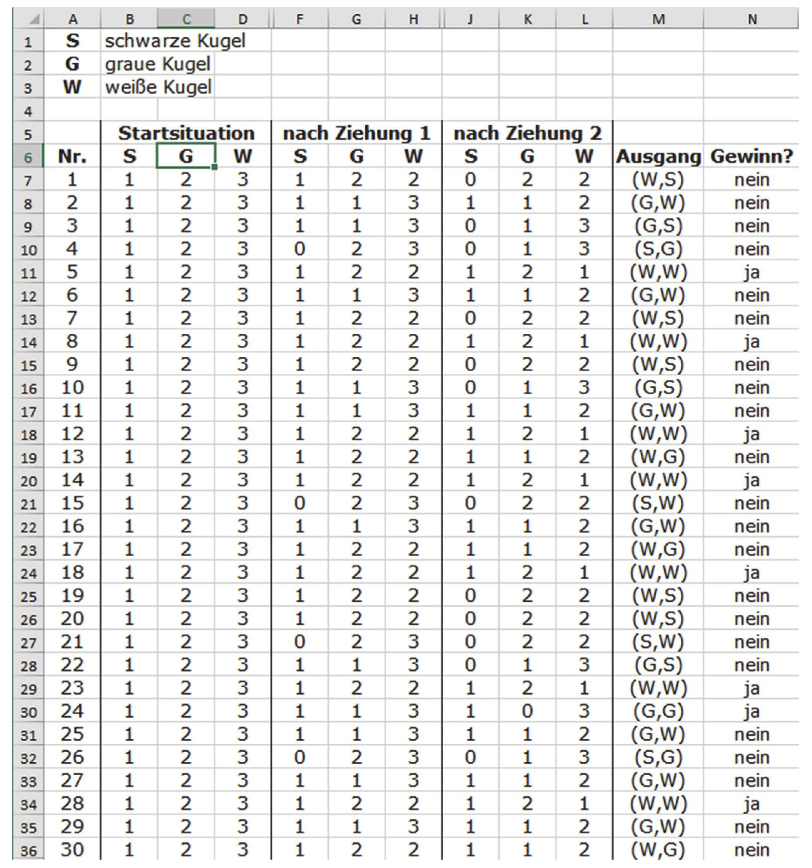
1. Gib an, wie viele schwarze Kugeln beim zehnten Spiel nach der ersten Ziehung noch in der Schachtel waren. (1 Punkt)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grafiken, Zeichnungen und Tabellen
  Ablesen des Wertes aus der Tabelle:
  Schreibe den Wert in die Lücke.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies den Wert aus der Tabelle in Zeile 16 ab.
2. Berechne den Prozentsatz der simulierten Spiele, bei denen keine graue Kugel gezogen wurde. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung mittels Formeln
  Wenn keine graue Kugel gezogen wurde, steht in der Spalte K eine $2$ . Bei $14$ von $30$ Spielen wurde keine graue Kugel gezogen, siehe Tabelle.
  Berechnen des Prozentsatzes:
  $\mathrm{p=\dfrac{W}{G}}\cdot100\ \%$ $\quad$ Einsetzen der bekannten Größen in die Formel
  $\mathrm{p=\dfrac{14}{30}\cdot100\ \%\quad\Rightarrow p\approx46{,}7\ \%}$
  Der Prozentsatz der simulierten Spiele, bei denen keine graue Kugel gezogen wurde, betragt: $\boxed{46{,}7\ \%}.$
  Schreibe den Wert in die Lücke.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Nimm die Tabelle zu Hilfe.
  Zähle die Spiele bei denen keine graue Kugel gezogen wurde. Berechne den Prozentsatz.
3
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Es wird überlegt, für jedes Spiel Punkte zu vergeben:
0 Punkte für verschiedenfarbige Kugeln
1 Punkt für zwei weiße Kugeln
2 Punkte für zwei graue Kugeln
In 20 Spielen wurden nacheinander folgende Punktzahlen erzielt:
$1{,}0,0{,}0,1{,}1,0{,}2,0{,}0,0{,}0,0{,}0,0{,}0,0{,}0,1{,}1$
1. Berechne, wie viele Punkte durchschnittlich in diesen 20 Spielen erzielt wurden. (1 Punkt)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Durchschnitt
  Berechnen des Durchschnitts
  $\mathrm{\dfrac{Summe\ der\ Punktzahlen}{Anzahl\ Spiele}=\dfrac{7}{20}=0{,}35}$
  Der Durchschnitt, der in den $20$ Spielen erzielt wurde, beträgt: $\ \boxed{0{,}35}.$
  Schreibe den Wert in die Lücke.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den arithmetischen Mittelwert. (Durchschnitt)
2. Yasmine hat im Mathematik-Unterricht gelernt, einen anderen Mittelwert als den Durchschnitt zu bestimmen. Er heißt "Median". Dazu werden alle Zahlen der Größe nach sortiert aufgeschrieben. Bei einer geraden Anzahl von Spielen ist der Median der Durchschnitt der beiden Zahlen, die in der Mitte stehen.
  Bestimme den Median für diese 20 Punktzahlen. (1 Punkt)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Median
  Bestimmen des Medians:
  Schreibe die Zahlen der Größe nach geordnet auf.
  $\small0, 0, 0, 0, 0, 0, 0, 0, 0, \large 0, 0, \small 0, 0, 0, 1, 1, 1, 1, 1, 2$
  
  Da es sich hier um eine gerade Anzahl von Zahlen handelt ist der Median
  der arithmetische Mittelwert der $10.$ und der $11.$ Zahl.
  $\mathrm{10. Zahl=0;\quad11.Zahl=0}\quad\Rightarrow \boxed{\mathrm{Median=0}}$
  Schreibe den Wert in die Lücke.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ordne die Zahlen ihrer Größe nach und bestimme den arithmetischen Mittelwert der $10.$ und der $11.$ Zahl.
3. Bei einem anderen Spiel wurden folgende Werte ermittelt:
  Durchschnitt: 0,5
  Median: 0
  Begründe, warum der Median in diesem Fall nicht aussagekräftig ist. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Median
  Begründung:
  Ist der Median gleich $0$ , so weiß man, dass mehr als $50\ \%$ der Spiele
  verloren wurden. Es kann aber keine Aussage darüber getroffen werden,
  bei wie vielen Spielen ein oder zwei Punkte erzielt wurden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
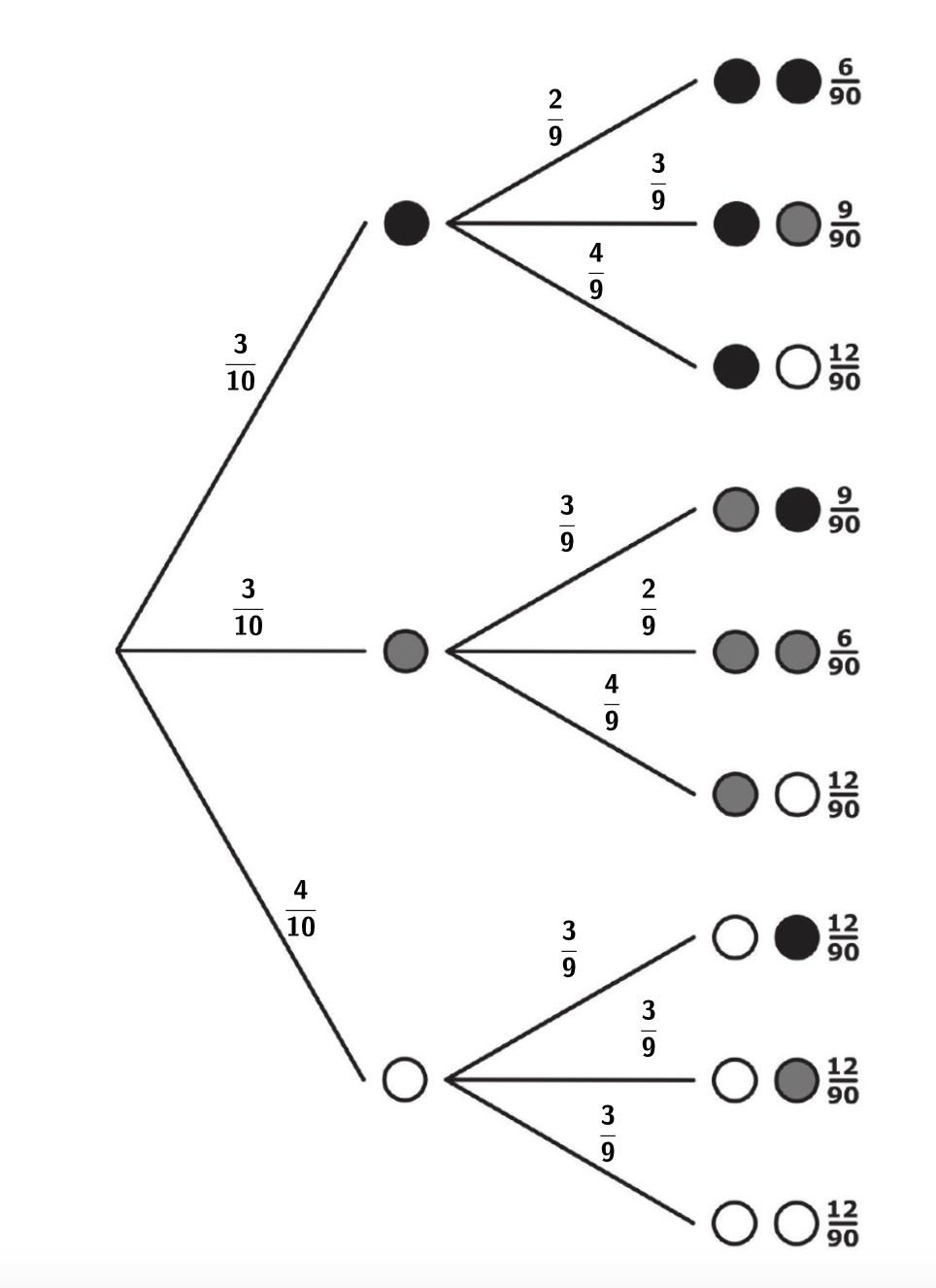
Für eine weitere Variante wurde ebenfalls ein Baumdiagramm angefertigt. Auch hierbei wurde die erste gezogene Kugel nicht wieder zurückgelegt.
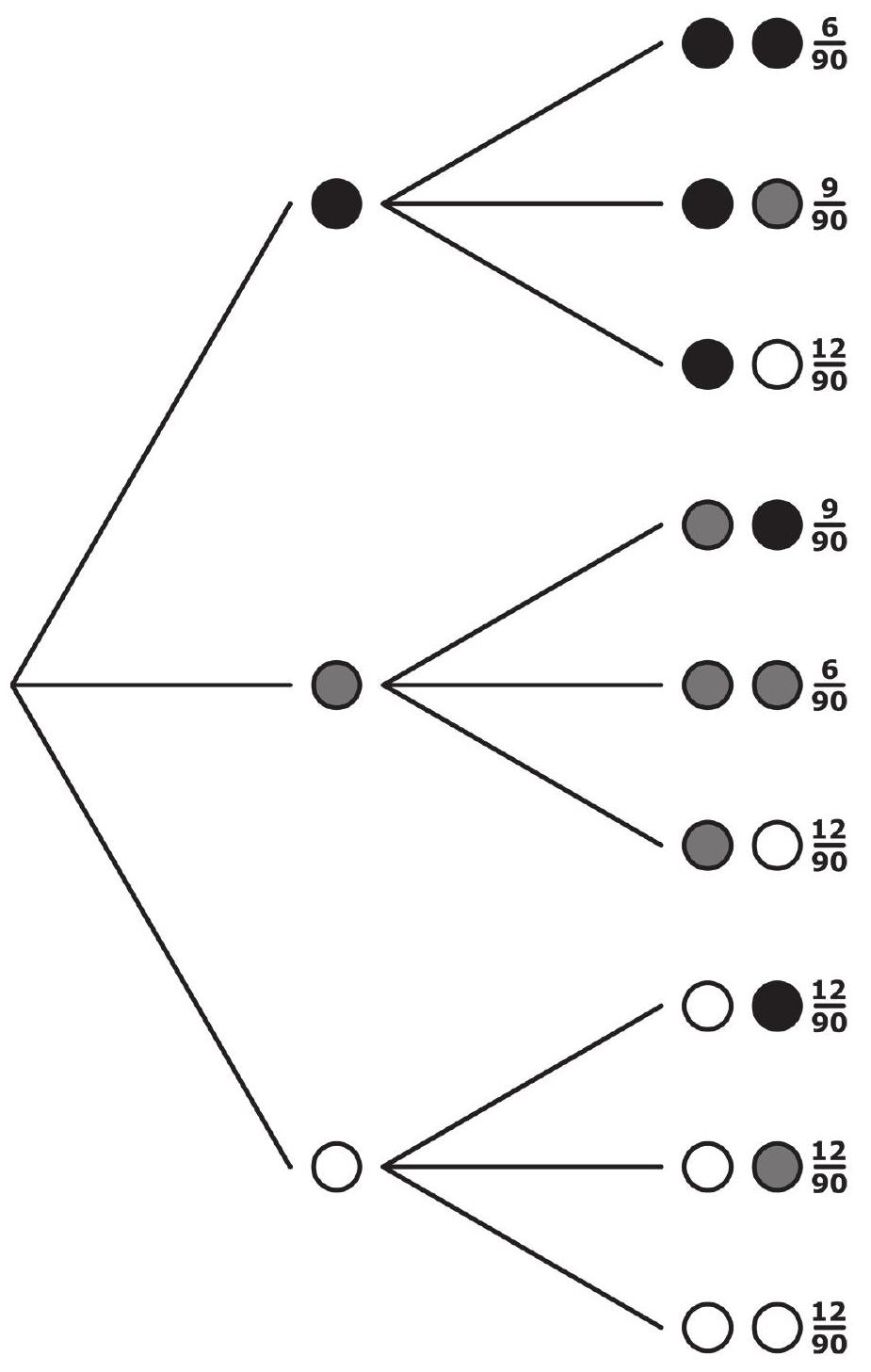
Gib eine Möglichkeit für die Anzahlen der schwarzen, der grauen und der weißen Kugeln in der Schachtel an. (2 Punkte)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Möglichkeit für die Anzahlen der schwarzen, der grauen und der weißen Kugeln in der Schachtel:
Da die Nenner jeweils $90=9\cdot10$ sind, kann man vermuten, dass sich insgesamt $10$ Kugeln in der Schachtel befinden - bei der ersten Ziehung gibt es $10$ , bei der zweiten danach noch $9$ Möglichkeiten.
Wenn du die Wahrscheinlichkeiten für die erste gezogene Farbe zusammenrechnest, erhältst du für schwarz und grau jeweils $\dfrac{27}{90}=\dfrac{3}{10}$ , für weiß $\dfrac{36}{90}=\dfrac{4}{10}$ .
Eine mögliche Kombination von Anzahlen ist also z. B.
$3$ schwarz, $3$ grau, $4$ weiß. (siehe Baumdiagramm)
Mit diesen Zahlen stimmen die vorgegebenen Wahrscheinlichkeiten mit der Rechnung überein.
Das Baumdiagramm braucht nicht erstellt zu werden.