Teil 2 Lineare Algebra und analytische Geometrie II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier.

Bei der Bearbeitung der Aufgaben dürfen Hilfsmittel verwendet werden.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Das Dach eines Hauses liegt in einer Ebene $H$ . In einem kartesischen Koordinatensystem des $ℝ^{3}$ ist die Ebene $H$ durch die drei Punkte $P (5 | 0 | 8)$ , $Q (5 | - 7,2 | 10)$ und $R (10 | - 10,8 | 11)$ festgelegt. Die Koordinaten der Punkte sind Längenangaben in der Einheit Meter.
Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden.
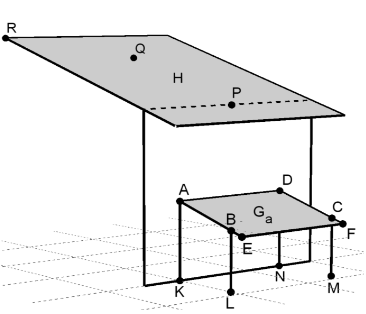
1. Ermitteln Sie jeweils eine Gleichung der Ebene $H$ in Parameter- und Koordinatenform und beschreiben Sie deren besondere Lage im Koordinatensystem.
  [ mögliches Teilergebnis: $H : 5 x_{2} + 18 x_{3} = 144$ ] (6 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene von Parameterform in Koordinatenform umwandeln
  Ermittle jeweils eine Gleichung der Ebene $H$ in Parameter- und Koordinatenform
  $E_{P Q R} : \vec{x} = \vec{O P} + r \cdot \vec{P Q} + s \cdot \vec{P R} = (\begin{array}{c} 5 \\ 0 \\ 8 \end{array}) + r \cdot (\begin{array}{c} 5 - 5 \\ - 7,2 - 0 \\ 10 - 8 \end{array}) + s \cdot (\begin{array}{c} 10 - 5 \\ - 10,8 - 0 \\ 11 - 8 \end{array})$
  Die Gleichung der Ebene $H$ in Parameterform lautet:
  $E_{P Q R} : \vec{x} = (\begin{array}{c} 5 \\ 0 \\ 8 \end{array}) + r \cdot (\begin{array}{c} 0 \\ - 7,2 \\ 2 \end{array}) + s \cdot (\begin{array}{c} 5 \\ - 10,8 \\ 3 \end{array})$
  Umwandlung in die Koordinatenform:
  Berechne den Normalenvektor ${\vec{n}}_{H}$ von $H$ :
  ${\vec{n}}_{H} = (\begin{array}{c} 0 \\ - 7,2 \\ 2 \end{array}) \times (\begin{array}{c} 5 \\ - 10,8 \\ 3 \end{array}) = (\begin{array}{c} 0 \\ 10 \\ 36 \end{array})$
  Dann ist $H : 0 \cdot x_{1} + 10 \cdot x_{2} + 36 \cdot x_{3} = d$
  Setze die Koordinaten des Punktes $P (5 | 0 | 8)$ ein, um $d$ zu berechnen:
  $0 + 0 + 36 \cdot 8 = d \Rightarrow d = 288$
  $\Rightarrow H : 10 \cdot x_{2} + 36 \cdot x_{3} = 288$
  Die Ebenengleichung kann noch durch $2$ dividiert werden.
  $\Rightarrow$ Die Gleichung der Ebene $H$ in Koordinatenform lautet dann:
  $H : 5 \cdot x_{2} + 18 \cdot x_{3} = 144 ✓$
  Beschreibe deren besondere Lage im Koordinatensystem
  Die Ebene $H$ ist echt parallel zur $x_{1}$ -Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Berechne $E_{P Q R} : \vec{x} = \vec{O P} + r \cdot \vec{P Q} + s \cdot \vec{P R}$ .
  Wandle dann in die Koordinatenform um.
  Teil 2
  Die $x_{1}$ -Komponente bei der Ebenengleichung tritt nicht auf.
  Was bedeutet das?
2. Die Größe des Neigungswinkels des Daches $H$ gegen die Horizontale muss gemäß einer örtlichen Bauvorschrift mindestens $15 °$ betragen. Zeigen Sie rechnerisch, dass die örtliche Bauvorschrift eingehalten wird. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von zwei Ebenen
  Zeige rechnerisch, dass die örtliche Bauvorschrift eingehalten wird
  Es ist ${\vec{n}}_{H} = (\begin{array}{c} 0 \\ 5 \\ 18 \end{array})$ der Normalenvektor der Ebene $H$ und $| \vec{n_{H}} | = \sqrt{0^{2} + 5^{2} + 18^{2}} = \sqrt{349}$ .
  $\vec{n_{x_{1} x_{2}}} = (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$ ist der Normalenvektor der $x_{1} x_{2}$ −Ebene und $| \vec{n_{x_{1} x_{2}}} | = 1$ .
  $\cos φ = \frac{| \vec{n_{H}} \circ \vec{n_{x_{1} x_{2}}} |}{| \vec{n_{H}} | \cdot | \vec{n_{x_{1} x_{2}}} |} = \frac{| (\begin{array}{c} 0 \\ 5 \\ 18 \end{array}) \circ (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) |}{\sqrt{349} \cdot 1} = \frac{18}{\sqrt{349}}$
  $φ = \cos^{- 1} (\frac{18}{\sqrt{349}}) \approx 15,52 °$
  Der Neigungswinkel der Ebene $H$ zum Boden beträgt rund $15,52 ° > 15 °$ .
  Die örtliche Bauvorschrift wird eingehalten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $\cos φ = \frac{| \vec{n_{H}} \circ \vec{n_{x_{1} x_{2}}} |}{| \vec{n_{H}} | \cdot | \vec{n_{x_{1} x_{2}}} |}$ $\Rightarrow φ$
  Vergleiche $φ$ mit $15 °$ .
3. Zur Überdachung der Terrasse $K L M N$ , die in der $x_{1} - x_{2}$ -Koordinatenebene liegt, wird ein rechteckiges Glasdach $A E F D$ , dessen Neigungswinkel verstellbar ist, aufgebaut. Das Glasdach liegt in der Ebene $G_{a} : (- 1,8 a + 9,9) x_{1} + (36 - 6 a) x_{2} + 10,8 x_{3} + 14,4 a = 119,16$
  mit dem Parameter $a \in ℝ$ . (3 BE)
  Die Ebenen $H$ und $G_{a}$ sollen parallel zueinander liegen. Ermitteln Sie hieraus den Wert des zugehörigen Parameters $a$ .
  [ Ergebnis: $a = 5,5$ ]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von zwei Ebenen
  Ermittle den Wert des zugehörigen Parameters $a$
  Gegeben sind $H : 5 \cdot x_{2} + 18 \cdot x_{3} = 144$ und $G_{a} : (- 1,8 a + 9,9) x_{1} + (36 - 6 a) x_{2} + 10,8 x_{3} + 14,4 a = 119,16$
  Wenn $H ∥ G_{a}$ , dann muss $- 1,8 a + 9,9 = 0$ sein $\Rightarrow a = \frac{9,9}{1,8} = 5,5$ .
  Dann ist $G_{5,5} : (36 - 6 \cdot 5,5) x_{2} + 10,8 x_{3} + 14,4 \cdot 5,5 = 119,16$ .
  Zusammengefasst folgt:
  $G_{5,5} : 3 x_{2} + 10,8 x_{3} = 39,96$
  Vergleiche die Normalenvektoren von $H$ und $G_{5,5}$ :
  $(\begin{array}{c} 0 \\ 5 \\ 18 \end{array}) = \frac{5}{3} \cdot (\begin{array}{c} 0 \\ 3 \\ 10,8 \end{array}) \Rightarrow H ∥ G_{a}$
  Der Wert des zugehörigen Parameters ist $a = 5,5$ .
  Anmerkung: Die beiden Ebenen sind echt parallel zueinander, da $39,96 \cdot \frac{5}{3} = 66,6 \neq 144$ ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Wenn $H ∥ G_{a}$ , dann muss die $x_{1}$ -Komponente von $G_{a}$ gleich null sein $\Rightarrow a$
  Berechne $G_{a}$ und vergleiche ${\vec{n}}_{H}$ mit ${\vec{n}}_{G_{a}}$ .
4. Zeigen Sie, dass die Punkte $A (8 | 0 | 3,7)$ und $B (8 | 3,42 | 2,75)$ in der Ebene $G_{5,5}$ liegen.
  (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung Punkt-Ebene (Inzidenz)
  Zeige, dass die Punkte $A (8 | 0 | 3,7)$ und $B (8 | 3,42 | 2,75)$ in der Ebene $G_{5,5}$ liegen
  Gegeben ist $G_{5,5} : 3 x_{2} + 10,8 x_{3} = 39,96$ .
  Setze die Koordinaten der Punkte in $G_{5,5}$ ein:
  $A$ eingesetzt: $3 \cdot 0 + 10,8 \cdot 3,7 = 39,96 ✓ \Rightarrow A \in G_{5,5}$ .
  $B$ eingesetzt: $3 \cdot 3,42 + 10,8 \cdot 2,75 = 10,26 + 29,7 = 39,96 ✓ \Rightarrow B \in G_{5,5}$ .
  Beide Punkte liegen in der Ebene $G_{5,5}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze die Koordinaten der Punkte in $G_{5,5}$ ein.
5. Für die folgenden Teilaufgaben gilt: $D (2 | 0 | 3,7)$ und $K (8 | 0 | 0)$ .
  Das Glasdach $A E F D$ ist festgelegt durch die Punkte $A$ , $E$ und $D$ . Aus statischen Gründen darf die Glasüberdachung nur um maximal $20 %$ der Länge von $A B$ über den Punkt $B$ hinausragen. Bestimmen Sie die Koordinaten des Punktes $E$ , wenn die maximal zulässige Länge vollständig ausgenutzt wird.
  Hinweis: $| \vec{A E} | = 1,2 \cdot | \vec{A B} |$ (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren und subtrahieren
  Bestimme die Koordinaten des Punktes $E$
  Es gilt: $| \vec{A E} | = 1,2 \cdot | \vec{A B} |$
  $\vec{O E} = \vec{O A} + \vec{A E} = \vec{O A} + 1,2 \cdot \vec{A B} = (\begin{array}{c} 8 \\ 0 \\ 3,7 \end{array}) + 1,2 \cdot (\begin{array}{c} 8 - 8 \\ 3,42 - 0 \\ 2,75 - 3,7 \end{array}) = (\begin{array}{c} 8 \\ 4,104 \\ 2,56 \end{array})$
  $\Rightarrow E (8 | 4,104 | 2,56)$
  Die Koordinaten des Punktes $E$ sind $E (8 | 4,104 | 2,56)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $\vec{O E} = \vec{O A} + \vec{A E} = \vec{O A} + 1,2 \cdot \vec{A B}$ .
6. Als Windschutz sollen die drei Seitenflächen $A K L B$ , $B L M C$ und $D N M C$ verglast werden. Der umbaute Raum besitzt die Form eines geraden trapezförmigen Prismas. Geben Sie die Koordinaten des Punktes $L$ an. Berechnen Sie die Materialkosten für die drei Seitenflächen, wenn der Preis $200 €$ pro $1 m^{2}$ beträgt. (6 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
  Gib die Koordinaten des Punktes $L$ an
  Der Punkt $L$ liegt senkrecht unterhalb vom Punkt $B$ in der $x_{1} x_{2}$ -Ebene $\Rightarrow L (8 | 3,42 | 0)$ .
  Die Koordinaten des Punktes $L$ sind $L (8 | 3,42 | 0)$ .
  Berechne die Materialkosten für die drei Seitenflächen, wenn der Preis $200 €$ pro $1 m^{2}$ beträgt
  Nach Aufgabe e) gilt: $D (2 | 0 | 3,7)$ und $K (8 | 0 | 0)$ .
  Es gibt zwei trapezförmige Seitenflächen mit gleichem Flächeninhalt und eine rechteckige Seitenfläche.
  Trapez:
  $A_{Trapez} = A_{A K L B} = \frac{| \vec{A K} | + | \vec{B L} |}{2} \cdot | \vec{K L} |$
  Berechne die Beträge der verwendeten Vektoren:
  $\vec{A K} = \vec{O K} + \vec{O A} = (\begin{array}{c} 8 \\ 0 \\ 0 \end{array}) - (\begin{array}{c} 8 \\ 0 \\ 3,7 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ - 3,7 \end{array}) \Rightarrow | \vec{A K} | = 3,7$
  $\vec{B L} = \vec{O L} + \vec{O B} = (\begin{array}{c} 8 \\ 3,42 \\ 0 \end{array}) - (\begin{array}{c} 8 \\ 3,42 \\ 2,75 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ - 2,75 \end{array}) \Rightarrow | \vec{B L} | = 2,75$
  $\vec{K L} = \vec{O L} + \vec{O K} = (\begin{array}{c} 8 \\ 3,42 \\ 0 \end{array}) - (\begin{array}{c} 8 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ - 3,42 \\ 0 \end{array}) \Rightarrow | \vec{K L} | = 3,42$
  $\Rightarrow A_{A K L B} = \frac{3,7 + 2,75}{2} \cdot 3,42 \approx 11,03 = A_{D N M C}$
  Rechteck:
  $A_{□} = A_{B L M C} = | \vec{L M} | \cdot | \vec{B L} |$
  Berechne die Beträge der verwendeten Vektoren:
  $| \vec{L M} | = | \vec{A D} | = \vec{O D} - \vec{O A} = (\begin{array}{c} 2 \\ 0 \\ 3,7 \end{array}) - (\begin{array}{c} 8 \\ 0 \\ 3,7 \end{array}) = (\begin{array}{c} - 6 \\ 0 \\ 0 \end{array}) \Rightarrow | \vec{L M} | = 6$
  $| \vec{B L} | = \vec{O L} - \vec{O B} = (\begin{array}{c} 8 \\ 3,42 \\ 0 \end{array}) - (\begin{array}{c} 8 \\ 3,42 \\ 2,75 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ - 2,75 \end{array}) \Rightarrow | \vec{B L} | = 2,75$
  $\Rightarrow A_{B L M C} = | \vec{L M} | \cdot | \vec{B L} | = 6 \cdot 2,75 = 16,5$
  $A_{g e s a m t} = 2 \cdot A_{Trapez} + A_{□} = 2 \cdot 11,03 + 16,5 = 38,56$
  Die drei Seitenflächen haben einen Gesamtflächeninhalt von $38,56 m^{2}$ .
  Die Kosten betragen dann: $K = 38,56 \cdot 200 = 7712$
  Die Materialkosten für die drei Seitenflächen, wenn der Preis $200 €$ pro $1 m^{2}$ beträgt, belaufen sich auf $7712 €$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Der Punkt $L$ liegt senkrecht unterhalb vom Punkt $B$ in der $x_{1} x_{2}$ -Ebene.
  Teil 2
  Es gibt zwei trapezförmige Seitenflächen mit gleichem Flächeninhalt und eine rechteckige Seitenfläche.
  Berechne den gesamten Flächeninhalt und multipliziere ihn mit $200$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil 2 Lineare Algebra und analytische Geometrie II

Ermittle jeweils eine Gleichung der Ebene H in Parameter- und Koordinatenform

Beschreibe deren besondere Lage im Koordinatensystem

Hast du eine Frage oder Feedback?

Zeige rechnerisch, dass die örtliche Bauvorschrift eingehalten wird

Hast du eine Frage oder Feedback?

Ermittle den Wert des zugehörigen Parameters a

Hast du eine Frage oder Feedback?

Zeige, dass die Punkte A(8|0|3,7) und B(8|3,42|2,75) in der Ebene G5,5 liegen

Hast du eine Frage oder Feedback?

Bestimme die Koordinaten des Punktes E

Hast du eine Frage oder Feedback?

Gib die Koordinaten des Punktes L an

Berechne die Materialkosten für die drei Seitenflächen, wenn der Preis 200€ pro 1 m2 beträgt

Hast du eine Frage oder Feedback?

Ermittle jeweils eine Gleichung der Ebene $H$ in Parameter- und Koordinatenform

Ermittle den Wert des zugehörigen Parameters $a$

Zeige, dass die Punkte $A (8 | 0 | 3,7)$ und $B (8 | 3,42 | 2,75)$ in der Ebene $G_{5,5}$ liegen

Bestimme die Koordinaten des Punktes $E$

Gib die Koordinaten des Punktes $L$ an

Berechne die Materialkosten für die drei Seitenflächen, wenn der Preis $200 €$ pro $1 m^{2}$ beträgt