Teil 2 Analysis 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgaben zum Ausdrucken als PDF findest du hier.
Bei der Bearbeitung der Aufgaben dürfen Hilfsmittel verwendet werden.
- 1
Gegeben ist die Funktion mit ihrer maximalen Definitionsmenge . Der Graph der Funktion wird mit bezeichnet.
Zeigen Sie, dass die Funktion keine Nullstellen besitzt und untersuchen Sie das Verhalten der Funktionswerte von bei links- und rechtsseitiger Annäherung an die Definitionslücke. Geben Sie die Art der Definitionslücke an. [5 BE]
Ermitteln Sie jeweils die Art und die Gleichung aller Asymptoten von .
[ Mögliches Teilergebnis: ] [4 BE]
Ermitteln Sie die maximalen Monotonieintervalle sowie jeweils die Art und die Koordinaten aller Extrempunkte von .
[Mögliches Teilergebnis: ] [8 BE]
Zeichnen Sie den Graphen unter Berücksichtigung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte sowie alle Asymptoten für - in ein kartesisches Koordinatensystem. Geben Sie die Wertemenge der Funktion an.
Maßstab auf beiden Achsen: [6 BE]
Gegeben ist die Funktion mit der Definitionsmenge .
1) Zeigen Sie, dass in eine Stammfunktion von ist. [3 BE]
2) Der Graph , die Gerade mit der Gleichung und die beiden Koordinatenachsen schließen im zweiten Quadranten ein endliches Flächenstück ein.
Kennzeichnen Sie dieses Flächenstück im Koordinatensystem aus Teilaufgabe 1 d) und berechnen Sie die Maßzahl des Inhalts dieses Flächenstücks auf zwei Nachkommastellen gerundet. [3 BE]
- 2
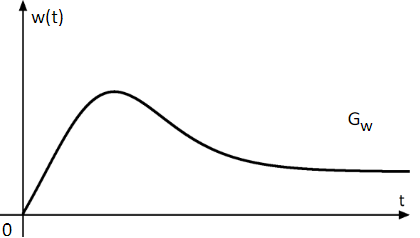
Nach Öffnung einer Schleuse gibt für die Funktion mit die zeitliche Entwicklung des Wasserdurchflusses in einem Kanal an einer Messstelle an. Der Wasserdurchfluss ist das Volumen des Wassers in , das an dieser Stelle pro Sekunde vorbeifließt. Die Zeit wird ab Öffnung der Schleuse zum Zeitpunkt in Sekunden gemessen. Die Abbildung zeigt einen Ausschnitt des Graphen der Funktion .
Bei allen Rechnungen kann auf das Mitführen von Einheiten verzichtet werden. Runden Sie alle Ergebnisse auf zwei Nachkommastellen.
Geben Sie den Wasserdurchfluss eine Sekunde nach Öffnung der Schleuse und für an. [2 BE]
Berechnen Sie den Zeitpunkt, zu dem der Wasserdurchfluss erstmals seit Beginn der Beobachtung den Wert von überschreitet. [4 BE]
Zeigen Sie, dass die Funktion auch durch die Gleichung dargestellt werden kann. [1 BE]
Berechnen Sie die Koordinaten des Hochpunktes von und interpretieren Sie diese im Sachzusammenhang. Hinweis: Der Nachweis, dass ein Hochpunkt vorliegt, muss nicht erbracht werden.
Mögliches Teilergebnis: [7 BE]
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


