Heft 2 - B1

🎓 Prüfungsbereich für Schleswig-Holstein

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Martha hat sich Gedanken über folgendes Viereck gemacht:
Die Zeichnung ist nicht maßstabsgetreu.
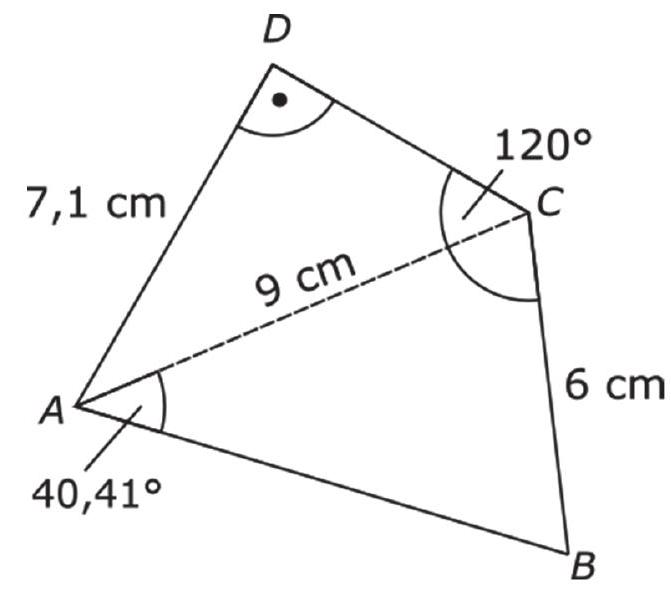
Martha hat herausgefunden: Die Strecke $\overline{C D}$ ist $5{,}53 \mathrm{~cm}$ lang.
1. Zeige, dass Martha recht hat. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
  Der Satz des Pythagoras angewendet auf das Dreieck $\ \text{ACD}$ lautet:
  $\mathrm{\overline{AC}^2=\overline{AD}^2+\overline{CD}^2\quad\Rightarrow \overline{CD}=\sqrt{\overline{AC}^2-\overline{AD}^2}}$
  Einsetzen der bekannten Werte
  $\mathrm{\overline{CD}=\sqrt{9^2-7{,}1^2}\ \ cm}$
  $\mathrm{\overline{CD}=5{,}53\ cm}$
  Die Strecke $\mathrm{\overline{CD}}$ ist $\boxed{\mathrm{5{,}53\ cm}}$ lang. Martha hat also recht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Das Dreieck $\text{ACD}$ ist ein rechtwinkliges Dreieck. Berechne die Strecke $\mathrm{\overline{CD}}$ mit dem Satz des Pythagoras.
2. Beschreibe einen anderen Lösungsweg, die Länge der Strecke $\overline{C D}$ zu ermitteln.
  Die Rechnung muss nicht ausgeführt werden.
  Ergänze dazu gegebenenfalls die Bezeichnungen in der Planskizze. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens im rechtwinkligen Dreieck
  Möglicher anderer Lösungsweg zur Berechnung der Strecke $\mathrm{\overline{CD}}$
  Berechnen des Winkels $\mathrm{\sphericalangle CAD}:$
  $\mathrm{cos(\sphericalangle{CAD})=\dfrac{7{,}1}{9}}\ ;$
  Berechnen der Strecke $\mathrm{\overline{CD}}:$
  $\mathrm{\overline{CD}=sin{\sphericalangle{CAD}\cdot 9}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne zuerst den Winkel $\mathrm{CAD}$ , dann die Strecke $\mathrm{\overline{CD}}.$
2
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Martha möchte den Umfang des Vierecks $A B C D$ bestimmen. Dazu berechnet sie die Länge der Strecke $\overline{A B}$ mit dem Kosinussatz.
1. Fülle die drei Lücken in Marthas Beschreibung aus:
  "Ich berechne zuerst $\measuredangle D C A$ über $\sin (\measuredangle D C A)=$ _____
  dann berechne ich den Winkel $\measuredangle$ _____ über $120^{\circ}-\measuredangle D C A$ ;
  dann $|\overline{A B}|^{2}=$ _____
  $\Rightarrow|\overline{A B}| \approx 8{,}74 \mathrm{~cm}$
  (3 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens im rechtwinkligen Dreieck
  Für den Sinus im Dreieck $\mathrm{DCA}$ gilt : $\ \mathrm{\sin (\measuredangle D C A)}=\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}=\boxed{\dfrac{7{,}1}{9}}$ $\measuredangle DCA\approx52{,}1^\circ$
  $\mathrm{120^\circ=\measuredangle{DCA+\measuredangle{ACB}}\quad\Rightarrow \measuredangle{\boxed{\text{ACB}}}=120^\circ-\measuredangle{DCA}}\approx 67{,}9^\circ$
  Für den Kosinussatz im Dreieck $\mathrm{DCA}$ gilt: $\mathrm{|\overline{A B}|^{2}=\boxed{9^2+6^2-2\cdot 9\cdot6\cdot \mathrm{cos{(\measuredangle{ACB})}}}} \quad\Rightarrow\mathrm{|\overline{AB}|\approx8{,}74\ cm}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Anwenden des Sinus im rechtwinkligem Dreieck
  Der Winkel $120^\circ$ setzt sich zusammen aus dem Winkel $\mathrm{\measuredangle{ACB}}$ und dem Winkel $\mathrm{\measuredangle{DCA}}.$
  Anwenden des Kosinussatzes.
2. Berechne den Umfang des Vierecks $A B C D$ . (1 Punkt)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Viereck
  Berechnen des Umfangs des Vierecks $\text{ABCD}$
  $\mathrm{U_{ABCD}=\overline{AB}+\overline{BC}+\overline{CD}+\overline{DA}}$ setze die Zahlenwerte in die Formel ein und $\hspace{44mm}$ berechne den Umfang.
  $\mathrm{U_{ABCD}=8{,}74+6+5{,}53+7{,}1\ [cm]\approx27{,}37\ cm}$
  Der Umfang des Vierecks $\text{ABCD}$ beträgt ca. $\boxed{\mathrm{27{,}37\ cm}}.$
  Schreibe den Wert in die Lücke.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Umfang des Vierecks $\text{ABCD}$ , indem Du die $4$ Seiten addierst.
3. Gib eine andere Möglichkeit an, die Länge der Strecke $\overline{A B}$ rechnerisch zu bestimmen.
  Die Rechnung muss nicht ausgeführt werden. (1 Punkt)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
  Andere Möglichkeit die Länge der Strecke $\mathrm{\overline{AB}}$ rechnerisch zu bestimmen:
  Berechne den Winkel $\text{DCA}$ :
  $\sin (\measuredangle D C A)=\left(\dfrac{7{,}1}{9}\right)$
  Berechne den Winkel $\text{ACB}:$
  $\quad\mathrm{\measuredangle{ACB}=120°-\measuredangle{DCA}}$
  Berechne die Strecke $\mathrm{\overline{AB}}$ mit dem Sinussatz:
  $\quad\mathrm{\dfrac{\overline{AB}}{sin(\measuredangle{ACB})}=\dfrac{6}{sin(40{,}41°)}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die die Strecke $\mathrm{\overline{AB}}$ mithilfe des Sinussatzes.

Um den Flächeninhalt des Vierecks $A B C D$ zu bestimmen, werden die Teildreiecke $A C D$ und $A B C$ betrachtet.

Bestimme den Flächeninhalt des Dreiecks $A C D$ . (2 Punkte)

Weise nach, dass im Dreieck $A B C$ die Höhe auf der Seite $\overline{A C}$ $5{,}67 \mathrm{~cm}$ lang ist. (1 Punkt)

Berechne den Flächeninhalt des Vierecks $A B C D$ . (3 Punkte)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle A_{ACD}$	$=$	$\displaystyle \dfrac{1}{2} \cdot \text{Kathete\,}_1 \cdot \text{Kathete\,}_2$
	↓	Einsetzen der Werte
$\displaystyle A_{ACD}$	$=$	$\displaystyle \dfrac{1}{2} \cdot 7{,}1 \cdot 5{,}53$
$\displaystyle A_{ACD}$	$≈$	$\displaystyle 19{,}63$

$\displaystyle \frac{h}{8{,}74}$	$=$	$\displaystyle \sin(40{,}41^{\circ})$	$\displaystyle \cdot 8{,}74$
$\displaystyle h$	$=$	$\displaystyle \sin(40{,}41^\circ) \cdot 8{,}74$
$\displaystyle h$	$≈$	$\displaystyle 5{,}67$

$\displaystyle A_{ABC}$	$=$	$\displaystyle \dfrac{1}{2} \cdot 9 \cdot 5{,}67$
$\displaystyle A_{ABC}$	$≈$	$\displaystyle 25{,}52$

$\displaystyle A_{ABCD}$	$≈$	$\displaystyle A_{ABC}+A_{ACD}$
$\displaystyle A_{ABCD}$	$≈$	$\displaystyle 25{,}52 + 19{,}63$
$\displaystyle A_{ABCD}$	$≈$	$\displaystyle 45{,}15$

Heft 2 - B1

Hast du eine Frage oder Feedback?

Möglicher anderer Lösungsweg zur Berechnung der Strecke CD‾\mathrm{\overline{CD}}CD

Berechnen des Winkels ∢CAD:\mathrm{\sphericalangle CAD}:∢CAD:

Berechnen der Strecke CD‾:\mathrm{\overline{CD}}: CD:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnen des Umfangs des Vierecks ABCD\text{ABCD}ABCD

Hast du eine Frage oder Feedback?

Andere Möglichkeit die Länge der Strecke AB‾\mathrm{\overline{AB}}AB rechnerisch zu bestimmen:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Möglicher anderer Lösungsweg zur Berechnung der Strecke $\mathrm{\overline{CD}}$

Berechnen des Winkels $\mathrm{\sphericalangle CAD}:$

Berechnen der Strecke $\mathrm{\overline{CD}}:$

Berechnen des Umfangs des Vierecks $\text{ABCD}$

Andere Möglichkeit die Länge der Strecke $\mathrm{\overline{AB}}$ rechnerisch zu bestimmen: