B II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Im $\mathbb{R}^3$ sind die Punkte $A (3 ∣ 2 ∣ 4), B (3 ∣ – 2 ∣ 2)$ und die Gerade $g:\vec{x} = \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}+r\begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}$ mit $r\in\mathbb{R}$ gegeben.
1. Die Gerade $h$ verläuft durch die Punkte $A$ und $B$ . Ermitteln Sie eine Gleichung der Geraden $h$ und geben Sie die besondere Lage der Geraden $g$ im Koordinatensystem an.
2. Untersuchen Sie die gegenseitige Lage der Geraden $g$ und $h$ .
3. Die beiden Geraden $g$ und $h$ spannen die Ebene $E$ auf. Ermitteln Sie eine Gleichung dieser Ebene in Koordinatenform.
  [ Mögliches Ergebnis: $E : x_{1} + x_{2} - 2 x_{3} + 3 = 0$ ]
4. Der Punkt $C (2 ∣ 1 ∣ 3)$ ist der Aufpunkt der Geraden $g$ . Bestimmen Sie die Koordinaten des Punktes $A$ *, der sich durch Spiegelung von $A$ an $C$ ergibt, und begründen Sie ohne weitere Rechnung, dass der Punkt $A$ * in der Ebene $E$ liegt.
5. Fertigen Sie eine aussagekräftige Skizze an, in der die gegenseitige Lage der Ebene $E$ , der Geraden $g$ und $h$ sowie der Punkte $A, A$ * und $C$ erkennbar ist. Verwenden Sie kein Koordinatensystem.
6. Gegeben ist die Ebenenschar $F_{a} : x_{1} + a^{2} x_{2} - 2 x_{3} + a + 2 = 0$ mit $a\in\mathbb{R}$ . Untersuchen Sie die gegenseitige Lage der Ebenen $E$ und $F_{a}$ in Abhängigkeit von $a$ .
2
Ein landwirtschaftlicher Betrieb ( $L$ ), eine Mühle ( $M$ ) und eine Bäckerei ( $B$ ) sind untereinander und mit dem Markt nach dem Leontief-Modell verbunden. Folgende Verflechtungstabelle stellt die Beziehungen zwischen den einzelnen Sektoren dar (alle Angaben in Mengeneinheiten ME):
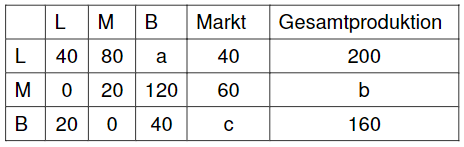
1. Bestimmen Sie die Werte von $a, b$ und $c$ und geben Sie deren Bedeutung im Sinne der vorliegenden Thematik an.
2. Beim landwirtschaftlichen Betrieb beträgt der gesamte Erlös 240.000 €. Dabei erzielt er pro ME am Markt doppelt so viel wie er von der Bäckerei bzw. der Mühle erhält. Berechnen Sie, wie hoch die Einnahmen des landwirtschaftlichen Betriebs am Markt pro ME sind.
3. Der landwirtschaftliche Betrieb stellt seinen Hof auf biologischen Anbau um und produziert deshalb ein Viertel ME weniger als bisher. Die Mühle produziert infolgedessen 40 ME weniger als bisher.
  1) Bestimmen Sie, in welchem Intervall sich dann die möglichen Produktionszahlen der Bäckerei bewegen.
  2) Durch die Umstellung lässt sich am Markt ein höherer Preis für die Produkte von $L$ von nun 3000 € pro ME erzielen. Weiterhin zahlen die Abnehmer Mühle und Bäckerei jeweils die Hälfte des Marktpreises für eine ME von $L$ . Prüfen Sie, ob die Umstellung zu einer Verringerung der Einnahmen führt (vgl. Teilaufgabe 2.b), wenn man davon ausgeht, dass die Bäckerei 60 ME insgesamt produziert.
4. Nach der erfolgreichen Umstellung auf Bio-Anbau verkauft der landwirtschaftliche Betrieb im folgenden Jahr mehr in seinem Hofladen, sodass die Marktabgabe auf 52 ME steigt. Sowohl die Mühle als auch die Bäckerei hingegen leiden an starker sich im Umland ansiedelnder Konkurrenz. Deshalb gibt die Mühle nur noch 39 ME und die Bäckerei 78 ME an den Markt ab. Bestimmen Sie die daraus resultierenden Produktionszahlen der drei Betriebe.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?