A I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier.

1
Gegeben ist die reelle Funktion $f$ durch $f (x) = (x^{2} - 2 x - 3) e^{- 0,5 x} = (x + 1) (x - 3) e^{- 0,5 x}$ mit der maximalen Definitionsmenge $D_{f} = ℝ$ . Ihr Graph ist $G_{f}$ . Runden Sie Ihre Ergebnisse gegebenenfalls auf zwei Nachkommastellen.
1. Geben Sie die Nullstellen der Funktion $f$ an und untersuchen Sie das Verhalten der Funktionswerte $f (x)$ für $x \to + \infty$ und $x \to - \infty$ .
2. Berechnen Sie Art und Koordinaten aller Extrempunkte von $G_{f}$ .
  [ mögliches Teilergebnis: $f^{'} (x) = - 0,5 (x^{2} - 6 x + 1) e^{- 0,5 x}$ ]
3. Zeichnen Sie $G_{f}$ für $- 2 \leq x \leq 12$ unter Verwendung vorliegender Ergebnisse in ein kartesisches Koordinatensystem.
4. Gegeben ist die Funktion $g : x \mapsto 5 \cdot e^{- 0,5 x}$ . Ihr Graph ist $G_{g}$ . Berechnen Sie die Koordinaten der Schnittpunkte der Graphen $G_{f}$ und $G_{g}$ und zeichnen Sie den Graphen $G_{g}$ in das Koordinatensystem der Teilaufgabe 1.c) ein.
  [Teilergebnis: $x_{1} = - 2$ und $x_{2} = 4$ ]
5. Zeigen Sie, dass die Funktion $F : x \mapsto F (x) = - 2 e^{- 0,5 x} (x + 1)^{2}$ mit $D_{f} = D_{F}$ eine Stammfunktion der Funktion $f$ ist.
6. Die Graphen $G_{f}$ und $G_{g}$ schließen ein endliches Flächenstück ein, das in allen vier Quadranten liegt. Schraffieren Sie dieses im Koordinatensystem der Teilaufgabe 1.c) und berechnen Sie die zugehörige Flächenmaßzahl auf zwei Nachkommastellen gerundet.
2
Die Abbildung zeigt den Graphen einer gebrochen-rationalen Funktion $h : x \mapsto h (x) = 0,25 x + 0,75 + \frac{a}{x + b}$ , $D_{h, m a x} \subset ℝ$ mit seiner schiefen Asymptote $y = 0,25 x + 0,75$ und der weiteren Asymptote $x = 1$ . Es gilt $a, b \in ℝ$ . Alle abzulesenden Werte sind ganzzahlig.
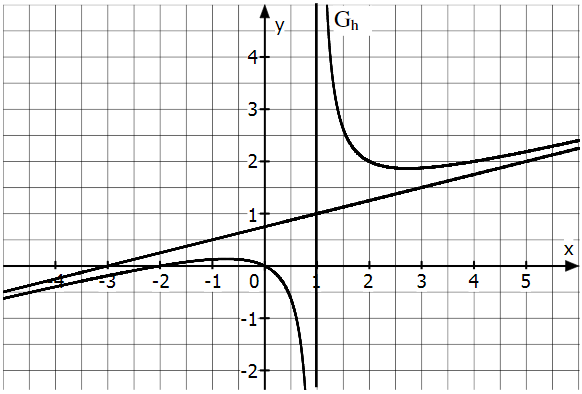
1. Aus der Gleichung der schiefen Asymptote können $\lim_{n \to \infty} (h (x) - (0,25 x + 75))$ und $\lim_{n \to \infty} h^{'} (x)$ gefolgert werden. Geben Sie diese Grenzwerte an und begründen Sie Ihre Ergebnisse.
2. Für diese Teilaufgabe gilt $x > 1$ . Lesen Sie aus der Abbildung die Lösungsmenge der Ungleichung $h (x) < 2$ ab.
3. Bestimmen Sie die Parameter $a$ und $b$ und geben Sie die Funktionsgleichung der Funktion $h$ an.
4. Gegeben ist die Funktion $k$ mit $k (x) = \ln (h (x))$ in ihrer maximalen Definitionsmenge $D_{k} \subset ℝ$ . Ihr Graph ist $G_{k}$ . Geben Sie die Definitionsmenge $D_{k}$ von $k$ und die Gleichungen der senkrechten Asymptoten von $G_{k}$ an.
3
In hochwertige Edelstahlfläschchen
sollen jeweils $100 {cm}^{3}$ Parfüm abgefüllt werden. Die Form des Fläschchens ist durch einen geraden Kreiszylinder
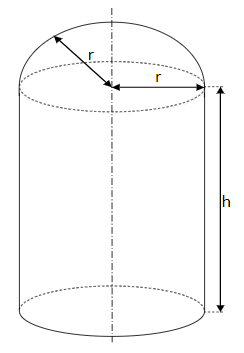
mit einer oben aufgesetzten Halbkugel vorgegeben. Die Aussparung für den Sprühkopf wird nicht berücksichtigt. Für die Oberfläche $O$ (in ${cm}^{2}$ ) des Fläschchens in Abhängigkeit von seinem Radius $r$ (in $cm$ ) erhält man die Funktionsgleichung $O (r) = \frac{5}{3} π r^{2} + \frac{200}{r}$ mit der Definitionsmenge $D_{O} =] 0; 3,5]$ . Auf die Mitführung von Einheiten wird verzichtet. Runden Sie gegebenenfalls Ihre Ergebnisse auf zwei Stellen nach dem Komma.
1. Bestimmen Sie das Verhalten von $O (r)$ für $r \to 0$ .
2. Berechnen Sie den Radius $r$ , für den die Oberfläche $O$ den absolut kleinsten Wert annimmt, und bestätigen Sie, dass $O_{min} \approx 112,23 ({cm}^{2})$ gilt.
3. Erstellen Sie für $1 \leq r \leq 3,5$ eine Wertetabelle mit der Schrittweite $∆ r = 0,5$ . Zeichnen Sie den Graphen der Funktion $O$ in ein Koordinatensystem im angegebenen Bereich. Wählen Sie hierfür einen geeigneten Maßstab.
4. Der Parfümhersteller möchte aus optischen Gründen den Radius $r = 2 (cm)$ wählen. Berechnen Sie dafür den Mehrbedarf an Edelstahlblech im Vergleich zu $O_{min}$ in Prozent. Begründen Sie stichhaltig, dass für alle Radien mit $r \in [2; 3,5]$ weniger als $10 %$ Mehrbedarf an Blech im Vergleich zu $O_{min}$ benötigt werden.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?