Teil 2 Lineare Algebra und analytische Geometrie II
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
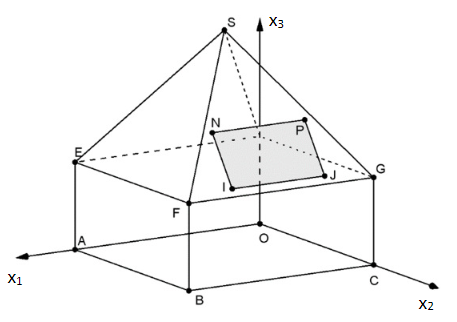
Ein Haus hat die Form eines Quaders mit oben aufgesetzter Pyramide. Das Haus wird modellhaft in einem kartesischen Koordinatensystem des betrachtet. Der Punkt liegt im Koordinatenursprung und die Punkte und liegen auf den Koordinatenachsen. Die Spitze liegt senkrecht über dem Mittelpunkt der durch die Punkte und festgelegten quadratischen Grundfläche des Hauses. Die südliche Dachfläche wird durch die Punkte , und begrenzt. Die Koordinaten sind Längenangaben in der Einheit Meter. Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden.
Der Bauherr geht davon aus, dass bei einer Dachflächenneigung von mindestens gegenüber der Grundfläche Schnee problemlos von der Dachfläche abrutschen kann. Untersuchen Sie, ob die Dachneigung des Hauses hierfür ausreicht.
- 2
Auf der südlichen Dachfläche (siehe Aufgabe 1) ist ein Sonnenkollektor angebracht, der durch das Rechteck dargestellt wird. Die Kante verläuft parallel zur Kante .
Ferner gilt: , ) und
Der Punkt ist der Mittelpunkt der Kante . Erläutern Sie, dass der Vektor mit Hilfe der Gleichung berechnet werden kann und bestimmen Sie die Koordinaten von .
[ Ergebnis: ]
Berechnen Sie den prozentualen Anteil der südlichen Dachfläche, die vom Sonnenkollektor bedeckt ist.
Die Position einer Satellitenanlage auf dem Dach eines Nachbarhauses lässt sich stark vereinfacht durch den Punkt beschreiben. Die Einstrahlrichtung der Sonne wird zum Zeitpunkt des vermuteten Leistungsmaximums des Sonnenkollektors durch den Vektor beschrieben. Untersuchen Sie durch Rechnung, ob der Schattenwurf der Satellitenanlage zum Zeitpunkt des vermuteten Leistungsmaximums innerhalb der Sonnenkollektorfläche liegt. Ermitteln Sie hierfür zunächst eine Gleichung der durch die südliche Dachfläche festgelegten Ebene in geeigneter Darstellungsform.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
