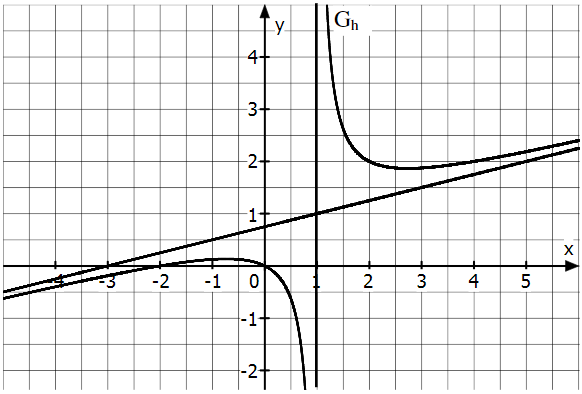
Aus der Gleichung der schiefen Asymptote können $${\displaystyle \underset{n\to \infty }{\lim }(h(x)-(\mathrm{0,25}x+75))}$$ und $${\displaystyle \underset{n\to \infty }{\lim }{h}^{\prime }(x)}$$ gefolgert werden. Geben Sie diese Grenzwerte an und begründen Sie Ihre Ergebnisse.

Für diese Teilaufgabe gilt $x>1$. Lesen Sie aus der Abbildung die Lösungsmenge der Ungleichung $h(x)<2$ ab.

Bestimmen Sie die Parameter $a$ und $b$ und geben Sie die Funktionsgleichung der Funktion $h$ an.

Gegeben ist die Funktion $k$ mit $k(x)=\ln (h(x))$ in ihrer maximalen Definitionsmenge $D_k\subset ℝ$. Ihr Graph ist $G_k$. Geben Sie die Definitionsmenge $D_k$ von $k$ und die Gleichungen der senkrechten Asymptoten von $G_k$ an.