Heft 2 - B1

🎓 Prüfungsbereich für Schleswig-Holstein

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Hier findest du die Aufgaben und Lösungen des Mathe ESA 2023 Prüfungsteil 2 Aufgabe 1.

Link zur Formelsammlung

Ein Taschenrechner ist in diesem Prüfungsteil erlaubt.

1
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Covid-19-Pandemie hat den Schulalltag in Schleswig-Holstein verändert. Der Schüler Maik erinnert sich an einige Besonderheiten aus dieser Zeit.
Zu Beginn des Schuljahres 2020/2021 durften alle Schülerinnen und Schüler wieder in die Schule. In einer Doppelstunde wurde insgesamt 15 Minuten gelüftet. In den Pausen blieben die Fenster geöffnet.
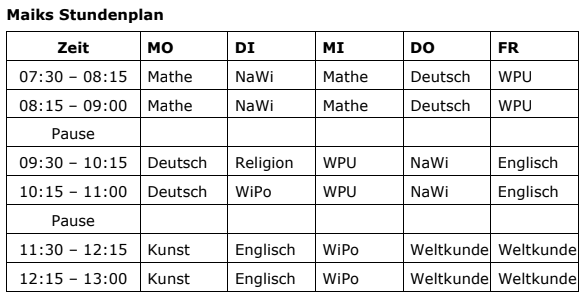
1. Bestimme mit Hilfe des Stundenplans, wie lange Maiks Klasse an einem Tag die Fenster geöffnet hatte. /2P.
  
  $3$ Doppelstunden: $3\cdot15=45$
  $2$ Pausen: $2\cdot30=60$
  Summe: $45 + 60 = 105$
  Maiks Klasse hatte die Fenster an einem Tag 105 Minuten geöffnet.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ermittle, wie viele Stunden Maiks Klasse die Fenster in einer Schulwoche geöffnet hatte.
  Falls du in a) keine Lösung finden konntest, rechne mit 105 Minuten weiter. /2P.
  
  $5\cdot105=525$
  $525 : 60 = 8,75$
  Maiks Klasse hatte die Fenster in einer Woche $8,75$ Stunden geöffnet.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Um das Ansteckungsrisiko zu reduzieren, wurden in der Schule zylinderförmige Behälter mit Desinfektionsmittel aufgestellt. Pro Benutzung wurden $5\ml$ Desinfektionsmittel gebraucht.
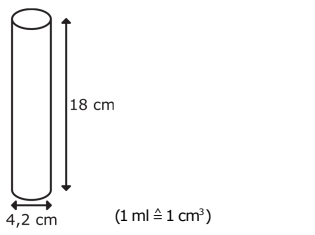
Berechne, wie oft der Behälter benutzt werden kann, bevor er leer ist. /3P.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
$V=r^2\pi\h$
$r = 4,2 : 2 = 2,1$
$V=2{,}1^2\cdot3{,}14\cdot18=249{,}38$
$249{,}38:5\approx49{,}88$
Der Desinfektionsmittelbehälter kann 49-mal benutzt werden, bevor er leer
ist.
Berechne das Volumen des Zylinders mit der entsprechenden Formel.
Dividiere das Volumne durch $5$ .
3
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Im Lockdown fanden alle 30 Unterrichtsstunden der Woche online statt. Dafür suchte Maik einen Datentarif. Er benötigte $0,3$ Gigabyte Datenvolumen pro Unterrichtsstunde. Er hatte die Wahl zwischen diesen beiden Angeboten.
1. Überprüfe, welcher Tarif für Maik nach vier Wochen günstiger gewesen wäre, wenn er ihn nur für den Unterricht verwendet hätte. /3P.
  
  Anzahl Unterrichtsstunden: 30 pro Woche
  Flatrate-Tarif: 30,50
  Sparfuchs29-Tarif:
  Anzahl Gigabyte in 4 Wochen: $0{,}3\cdot30\cdot4=36$
  Zusätzliche Kosten: $36 - 25 = 11$
  $11\cdot1{,}50=16{,}50$
  $16,50 + 9,99 = 26,49$
  Mit dem Sparfuchs29-Tarif hätte Maik $26,49$ € bezahlen müssen. Der Sparfuchs29-Tarif wäre für Maik günstiger gewesen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ermittle die Anzahl der Gigabyte, für die Maik zusätzlich bezahlen muss.
  Multipliziere diese mit dem Preis pro Gigabyte.
2. Ermittle, ab welcher Datenmenge sich der Flatrate-Tarif gelohnt hätte. /2P.
  
  $(30{,}50-9{,}99):1{,}5=13{,}67\approx14$
  $14 + 25 = 39$
  Ab $39$ Gigabyte hätte sich der Flatrate-Tarif für Maik gelohnt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Subtrahiere vom Faltrate- Tarif den Sparfuchs29-Tarif.
  Dividiere diese Differenz durch die Kosten für 1 Gigabyte beim Sparfuchs29-Tarif.
  Addiere den Wert zu den 25 Gigabyte, die im Sparfuch29-Tarif inclusiv sind.
4
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Wahlteil zu B1
Du musst einen der beiden Wahlteile bearbeiten.
Ab dem April 2021 durften alle 550 Schülerinnen und Schüler an Maiks Schule zurück in den Unterricht. Alle Schülerinnen und Schüler mussten sich zweimal pro Woche selbst testen. Am Ende der ersten Woche waren $98 %$ aller Tests negativ.
Berechne die Anzahl der positiven Tests nach der ersten Woche. /3P.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung mittels Formeln
Gesamtanzahl Tests: $550\cdot2=1100$
$W=p\cdot G$
Grundwert: $G = 1100$
Prozentsatz positive Tests: $p=2\%=0{,}02$
Prozentwert: $W=0{,}02\cdot1100=22$
In der ersten Woche waren $22$ Tests positiv.
Ermittle den Prozentwert anhand der Formel.
Beachte, dass die positiven Tests $2$ % betragen.
5
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Ab dem Schuljahr 2021/22 durfte im Unterricht wieder in Vierergruppen gearbeitet werden.
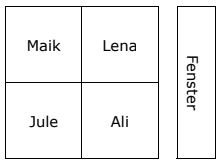
1. Bestimme die Anzahl der Möglichkeiten, wie sich Maik, Lena, Jule und
  Ali an ihren Vierertisch hinsetzen könnten. /2 P.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kombinatorik
  Die Gruppe besteht aus 4 Schülern. Die Anzahl der Möglichkeiten, wie sich die 4 Schüler an dem Vierertisch hinsetzen können, ergibt sich wie folgt.
  $4!=4\cdot3\cdot2\cdot1=24$
  Es gibt $24$ Möglichkeiten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Gib eine mögliche Bedingung für die Sitzordnung an, die die Anzahl der
  Möglichkeiten begrenzen würde. /1 P.
  
  Zum Beispiel: Am Fenster müssen immer ein Mädchen und ein Junge sitzen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉