Das kleine Quadrat in der Abbildung hat einen Flächeninhalt von .
Bestimme den Umfang des grau gefärbten Quadrats.
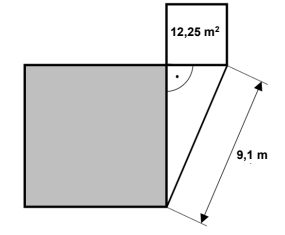
Hinweis: Skizze nicht maßstabsgetreu
Quelle: StMUK
Das kleine Quadrat in der Abbildung hat einen Flächeninhalt von .
Bestimme den Umfang des grau gefärbten Quadrats.

Hinweis: Skizze nicht maßstabsgetreu
Quelle: StMUK