B3

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Der in Abbildung 1 dargestellte Körper $K$ mit den Eckpunkten $A_{1}, A_{2}, A_{3}, A_{4}, B_{1}, B_{2}, B_{3}$ und $B_{4}$ hat folgende Eigenschaften:
$A_{1} A_{2} A_{3} A_{4}$ ist ein Rechteck in der $x_{1} x_{2}$ -Ebene, $B_{1} B_{2} B_{3} B_{4}$ ist ein Rechteck in einer zur $x_{1} x_{2}$ -Ebene parallelen Ebene. Die Vierecke $A_{2} A_{3} B_{3} B_{2}$ und $A_{1} A_{4} B_{4} B_{1}$ liegen in Ebenen, die parallel zur $x_{1} x_{3}$ -Ebene verlaufen.
Sechs der Eckpunkte sind gegeben durch
$A_{1}(50|-5| 0)$ , $A_{2}(50|5| 0)$ , $A_{3}\left(\frac{\sqrt{75}}{3}|5| 0\right)$ , $A_{4}\left(\frac{\sqrt{75}}{3}|-5| 0\right)$ , $B_{2}(10|5| 30)$ , $B_{3}\left(\frac{\sqrt{75}}{3}|5| 30\right)$ .
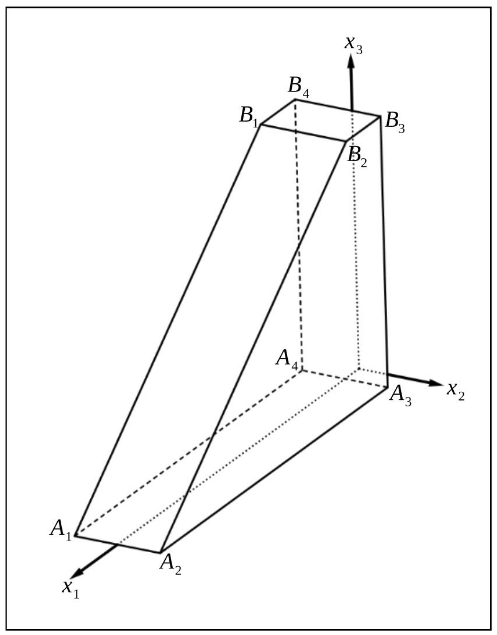
1. Geben Sie die Koordinaten des Punktes $B_{1}$ an. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Übersicht – Abiturkurs Geometrie
  Gib die Koordinaten des Punktes $B_{1}$ an
  $x_{1}$ -Koordinate von $B_{1}$ entspricht der $x_{1}$ -Koordinate von $B_{2} = 10$ .
  $x_{2}$ -Koordinate von $B_{1}$ entspricht der $x_{2}$ -Koordinate von $A_{4} = - 5$ .
  $x_{3}$ -Koordinate von $B_{1}$ entspricht der $x_{3}$ -Koordinate von $B_{2} = 30$ .
  Die Koordinaten des Punktes $B_{1}$ sind $B_{1}(10|-5| 30)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Suche passende, gegebene Vektoren.
2. Begründen Sie, dass die Seitenfläche $A_{2} A_{3} B_{3} B_{2}$ ein Trapez ist, und berechnen Sie das Volumen des Körpers $K$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
  Begründe, dass die Seitenfläche $A_{2} A_{3} B_{3} B_{2}$ ein Trapez ist
  Die Seitenfläche $A_{2} A_{3} B_{3} B_{2}$ ist ein Trapez mit $\overline{A_{2} A_{3}} \| \overline{B_{2} B_{3}}$ , wie anhand der $x_{2}$ - und $x_{3}$ -Koordinaten der Punkte ablesbar ist. (Siehe auch die Berechnung der entsprechenden Vektoren in nächsten Abschnitt.)
  
  Berechne das Volumen des Körpers $K$
  Berechne die Vektoren und ihre Beträge:
  $\overrightarrow{A_2A_3}=\begin{pmatrix}\frac{\sqrt{75}}{3}\\5\\0\end{pmatrix}-\begin{pmatrix}50\\5\\0\end{pmatrix}=\begin{pmatrix}\frac{\sqrt{75}}{3}-50\\0\\0\end{pmatrix}$ und $\left|\overline{A_{2} A_{3}}\right|=50-\frac{\sqrt{75}}{3} \approx 47{,}11$
  $\overrightarrow{B_2B_3}=\begin{pmatrix}\frac{\sqrt{75}}{3}\\5\\30\end{pmatrix}-\begin{pmatrix}10\\5\\30\end{pmatrix}=\begin{pmatrix}\frac{\sqrt{75}}{3}-10\\0\\0\end{pmatrix}$ und $\left|\overline{B_{2} B_{3}}\right|=10-\frac{\sqrt{75}}{3} \approx 7{,}11$
  $\overrightarrow{A_3B_3}=\begin{pmatrix}\frac{\sqrt{75}}{3}\\5\\30\end{pmatrix}-\begin{pmatrix}\frac{\sqrt{75}}{3}\\5\\0\end{pmatrix}=\begin{pmatrix}0\\0\\30\end{pmatrix}$ und $\left|\overline{A_{3} B_{3}}\right|=30$
  $\overrightarrow{A_1A_2}=\begin{pmatrix}50\\5\\0\end{pmatrix}-\begin{pmatrix}50\\-5\\0\end{pmatrix}=\begin{pmatrix}0\\10\\0\end{pmatrix}$ und $\left|\overline{A_{1} A_{2}}\right|=10$
  Es gilt: $V_{\text {Körper }}=A_{\text {Grundfläche }}\cdot h$
  $V_{\text {Körper }}=A_{\text {Trapez }} \cdot h=\frac{\left(\left|\overline{A_{2} A_{3}}\right|+\left|\overline{B_{2} B_{3}}\right|\right) \cdot\left|\overline{A_{3} B_{3}}\right|}{2} \cdot\left|\overline{A_{1} A_{2}}\right|$
  $V_{\text {Körper }}=\dfrac{\left(50-\frac{\sqrt{75}}{3}+10-\frac{\sqrt{75}}{3}\right)\cdot 30 }{2} \cdot 10\approx 8134$
  Das Volumen des Körpers $K$ beträgt rund $8134\;\mathrm{VE}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Es gilt: $\overline{A_{2} A_{3}} \| \overline{B_{2} B_{3}}$ , wie anhand der $x_{2}$ - und $x_{3}$ -Koordinaten der Punkte ablesbar ist.
  Teil 2
  Berechne die entsprechenden Vektoren und ihre Beträge.
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Gegeben sind $A_{2}(50|5| 0)$ und $B_{2}(10|5| 30)$ .
Der Körper $K$ ist Teil eines mathematischen Modells eines Architekturbüros zur Planung eines neuen Hotels. Das Hotel soll zehn Stockwerke gleicher Höhe besitzen. Für die an die Schrägen angrenzenden Hotelzimmer sind von der 1. bis zur 9. Etage Balkone geplant. Als Beispiel ist in Abbildung 2 der Boden des Balkons für die 3. Etage dargestellt.
Eine Längeneinheit im Modell entspricht einem Meter in der Realität.
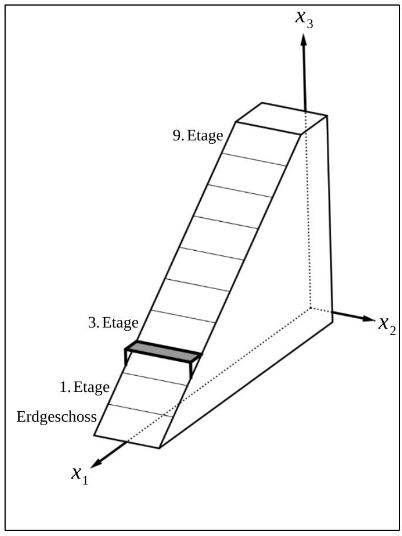
Abbildung 2
Durch $\def\arraystretch{1.25} E_{a}: \vec{x}=\left(\begin{array}{c}50-a \\ 5 \\ 0{,}75 \cdot a\end{array}\right)+r \cdot\left(\begin{array}{c}0 \\ -10 \\ 0\end{array}\right)+s \cdot\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right), a \in \mathbb{R}, r, s \in \mathbb{R}$ , ist eine Schar paralleler Ebenen gegeben. Der Boden jedes Balkons wird im Folgenden als Fläche innerhalb einer geeigneten Ebene der Schar modelliert. Der Boden des Balkons für die 3. Etage liegt z. B. in der Ebene $E_{12}$ .
1. Zeigen Sie: Für jeden Wert von a mit $0 \leq a \leq 40$ liegt der Punkt $(50-a|5| 0{,}75 \cdot a)$ auf der Strecke $\overline{A_{2} B_{2}}$ . (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungssysteme
  Zeige: Für jeden Wert von a mit $0 \leq a \leq 40$ liegt der Punkt $(50-a|5| 0{,}75 \cdot a)$ auf der Strecke $\overline{A_{2} B_{2}}$
  Der Vektor $\overrightarrow{A_{2} B_{2}}=\begin{pmatrix}10\\5\\30\end{pmatrix}-\begin{pmatrix}50\\5\\0\end{pmatrix}=\begin{pmatrix}-40\\0\\30\end{pmatrix}$ .
  Eine Parametergleichung der Strecke $\overline{A_{2} B_{2}}$ ist dann gegeben durch: $\overline{A_{2} B_{2}}: \vec{x}=\overrightarrow{OA_{2}}+t \cdot \overrightarrow{A_{2} B_{2}}=\begin{pmatrix}50\\5\\0\end{pmatrix}+t\cdot \begin{pmatrix}-40\\0\\30\end{pmatrix}, t \in \mathbb{R}, 0 \leq t \leq 1$ .
  Damit erhält man das Gleichungssystem:
  $\begin{pmatrix}50-a\\5\\0{,}75\cdot a\end{pmatrix}=\begin{pmatrix}50\\5\\0\end{pmatrix}+t\cdot \begin{pmatrix}-40\\0\\30\end{pmatrix}$ $\;\Rightarrow\;$ $\def\arraystretch{1.25} \left|\begin{array}{c}50-a =50-40\cdot t \\ 5=5 \\0{,}75 \cdot a= 30 \cdot t\end{array}\right|$ .
  Aus Gleichung $\mathrm{I}$ folgt $t=\dfrac{a}{40}$ .
  Mit Gleichung $\mathrm{III}$ erhält man den gleichen Wert für $t$ .
  Das Gleichungssystem hat somit die Lösung $t=\dfrac{a}{40}$ .
  Wegen $0 \leq a \leq 40$ gilt $0 \leq t \leq 1$ . Damit liegt für jedes $a \in \mathbb{R}$ mit $0 \leq a \leq 40$ der Punkt $(50-a|5|0{,}75\cdot a)$ auf der Strecke $\overline{A_{2} B_{2}}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Erstelle eine Parametergleichung der Strecke $\overline{A_{2} B_{2}}$ .
  Der Punkt $(50-a|5| 0{,}75 \cdot a)$ soll auf dieser Parametergleichung liegen $\;\Rightarrow\;$ löse das Gleichungssystem.
2. Die Menge aller Punkte der Bodenfläche des Balkons für die 3. Etage wird durch die Parametergleichung
  $\vec{x}=\begin{pmatrix}38 \\5 \\9\end{pmatrix}+r \cdot \begin{pmatrix}0 \\-10 \\0\end{pmatrix}+s \cdot \begin{pmatrix}1 \\0 \\0\end{pmatrix}, 0 \leq r \leq 1{,}0 \leq s \leq 3$
  beschrieben.
  Der Balkon ist wie in Abbildung 3 dargestellt auf zwei vertikalen Stützen $s_{1}$ und $s_{2}$ gelagert.
  Berechnen Sie die Länge der Stütze $\mathrm{s}_{1}$ . (4 P)
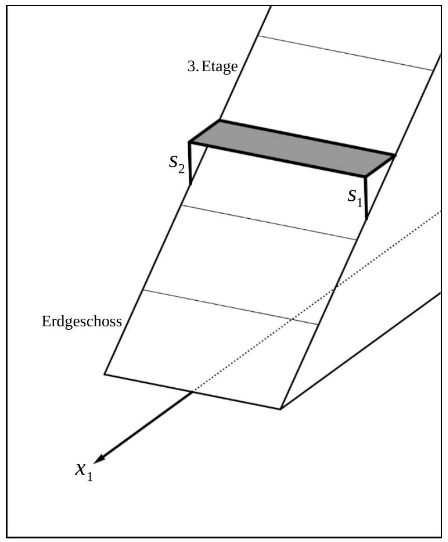
  Abbildung 3
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
  Berechne die Länge der Stütze $\mathrm{s}_{1}$
  Bekannt ist: Für jedes $a \in \mathbb{R}$ mit $0 \leq a \leq 40$ der Punkt $(50-a|5|0{,}75\cdot a)$ auf der Strecke $\overline{A_{2} B_{2}}$ .
  Ist $a = 12$ (wegen $E_{12}$ ), dann liegt der Punkt $(38 ∣ 5 ∣ 9)$ auf der Strecke $\overline{A_{2} B_{2}}$ .
  Der Punkt $(38 ∣ 5 ∣ 9)$ ist ein Eckpunkt der Bodenfläche des Balkons (für $r = 0$ und $s = 0$ ).
  Die Menge aller Punkte der Bodenfläche des Balkons für die 3. Etage wird durch die gegebene Parametergleichung für $0 \leq r \leq 1,0 \leq s \leq 3 0≤r≤1{,}0≤s≤3$ beschrieben, d.h. einen weiteren Balkoneckpunkt erhält man für $r = 0$ und $s = 3$ .
  $\vec{x}=\begin{pmatrix}38 \\5 \\9\end{pmatrix}+0 \cdot \begin{pmatrix}0 \\-10 \\0\end{pmatrix}+3 \cdot \begin{pmatrix}1 \\0 \\0\end{pmatrix}=\begin{pmatrix}41 \\5 \\9\end{pmatrix}$ $\;\Rightarrow\;C(41|5| 9)$
  Der Balkoneckpunkt $C (41 ∣ 5 ∣ 9)$ ist das obere Ende der Stütze $s_{1}$ .
  Die Stütze $s_{1}$ kann jetzt als Strecke modelliert werden, die in der Geraden $g: \vec{x}=\begin{pmatrix}41 \\ 5 \\ 9\end{pmatrix}+u \cdot\begin{pmatrix}0 \\ 0 \\ 1\end{pmatrix}, u \in \mathbb{R}$ enthalten ist.
  Für die Längenberechnung der Stütze braucht man den Schnittpunkt der Geraden $g$ mit der Parametergleichung der Strecke $\overline{A_{2} B_{2}}$ : $\begin{pmatrix}41 \\ 5 \\ 9\end{pmatrix}+u \cdot\begin{pmatrix}0 \\ 0 \\ 1\end{pmatrix}=\begin{pmatrix}50\\5\\0\end{pmatrix}+t\cdot \begin{pmatrix}-40\\0\\30\end{pmatrix}$
  Man erhält das Gleichungssystem:
  $\def\arraystretch{1.25} \left|\begin{array}{c}41=50-40 \cdot t \\ 5=5 \\ 9+u=30 \cdot t\end{array}\right|$
  Aus Gleichung $\mathrm{I}$ folgt $t=\dfrac{9}{40}$ .
  Gleichung $\mathrm{III}$ ergibt für $u$ den Wert $u=30\cdot\dfrac{9}{40}-9=-2{,}25$ .
  Da der Richtungsvektor der Geraden $g$ ein Einheitsvektor ist, entspricht $∣ u ∣ = 2,25$ der Länge der Stütze $s_{1}$ .
  Die Stütze $s_{1}$ besitzt eine Länge von $2{,}25 \mathrm{~m}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Menge aller Punkte der Bodenfläche des Balkons für die 3. Etage wird durch die gegebene Parametergleichung beschrieben.
  Einen weiteren Balkoneckpunkt erhält man für $r = 0$ und $s = 3$ .
  Dieser Balkoneckpunkt ist das obere Ende der Stütze $s_{1}$ .
  Erstelle eine Geradengleichung $g$ für die Stütze und berechne den Schnittpunkt mit der Parametergleichung der Strecke $\overline{A_{2} B_{2}}$ $\;\Rightarrow\;u_1$
  Da der Richtungsvektor der Geraden $g$ ein Einheitsvektor ist, entspricht $∣ u_{1} ∣$ der Länge der Stütze $s_{1}$ .
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1 und 2.
Das Hotel soll aus drei Gebäuden bestehen, die jeweils die gleiche Form besitzen. Durch den Körper $K$ wird Gebäude I modelliert, die Gebäude II und III sind gegenüber Gebäude I jeweils um $120^{\circ}$ gedreht (siehe Abbildung 4). Alle drei Gebäude stehen so aneinander, dass sie einen dreieckigen Innenhof bilden. In der Modellierung liegt dieser Innenhof in der $x_{1} x_{2}$ -Ebene.
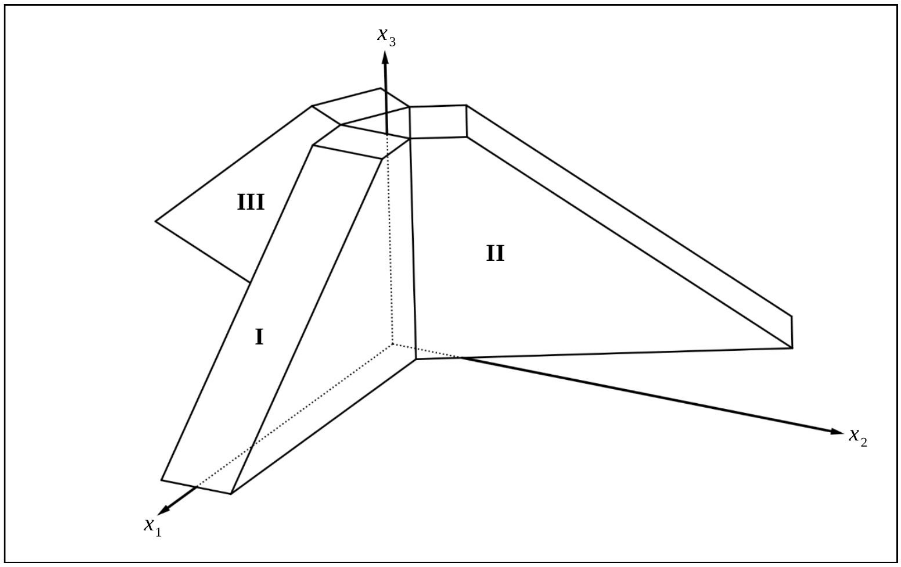
Abbildung 4
Die nebenstehende Abbildung 5 zeigt das Modell des Hotels von oben.
$\left(A_{3}\left(\frac{\sqrt{75}}{3}|5| 0\right), A_{4}\left(\frac{\sqrt{75}}{3}|-5| 0\right) \right)$
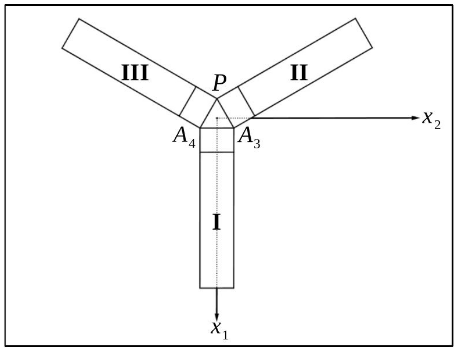
Abbildung 5
1. Der Innenhof $A_{4} A_{3} P$ hat die Form eines gleichseitigen Dreiecks.
  Ermitteln Sie rechnerisch die Koordinaten des Punktes $P$ .
  [Zur Kontrolle: $\left.P\left(-\frac{2 \cdot \sqrt{75}}{3}|0| 0\right) \approx P(-5{,}77|0| 0).\right]$ (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichseitiges Dreieck
  Ermittele rechnerisch die Koordinaten des Punktes $P$
  Bekannt ist: Der Innenhof $A_{4} A_{3} P$ hat die Form eines gleichseitigen Dreiecks.
  Aus Symmetriegründen muss der Punkt $P$ auf der $x_{1}$ -Achse liegen (siehe Abbildung 5).
  Die Differenz der $x_{2}$ -Koordinaten von $A_{3}$ und $A_{4}$ ist gleich $10$ , d.h. die Seiten des Dreiecks $A_{4} A_{3} P$ besitzen eine Länge von $\left|\overline{A_{3} A_{4}}\right|=10\;\mathrm{LE}$ .
  Die Höhe $h_{D}$ des Dreiecks $A_{4} A_{3} P$ wird mit dem Satz des Pythagoras berechnet:
  $h_{D}=\sqrt{10^{2}-5^{2}}=\sqrt{75}=5 \cdot \sqrt{3}$
  Die Höhe $h_{D}$ des Dreiecks $A_{4} A_{3} P$ beträgt $5 \cdot \sqrt{3}\;\mathrm{LE}$ .
  Der Höhenschnittpunkt im gleichseitigen Dreieck teilt jede Höhe im Verhältnis $2 : 1$ .
  Vom Koordinatenursprung aus gesehen hat $P$ die $x_{1}$ -Koordinate $p_1=-\dfrac{2}{3}\cdot h_D=-\dfrac{2}{3}\cdot \sqrt{75}$ .
  Damit gilt: $P\left(-\frac{2 \cdot \sqrt{75}}{3}\Big \vert0\Big \vert 0\right) \approx P(-5{,}77|0| 0)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Innenhof $A_{4} A_{3} P$ hat die Form eines gleichseitigen Dreiecks.
  Aus Symmetriegründen muss der Punkt $P$ auf der $x_{1}$ -Achse liegen (siehe Abbildung 3).
  Ermittele die Länge der Strecke $\overline{A_{3} A_{4}}$ .
  Die Höhe $h_{D}$ des Dreiecks $A_{4} A_{3} P$ wird mit dem Satz des Pythagoras berechnet.
  Der Höhenschnittpunkt im gleichseitigen Dreieck teilt jede Höhe im Verhältnis $2 : 1$ .
2. Berechnen Sie den Abstand von $A_{4}$ zum Koordinatenursprung $O (0 ∣ 0 ∣ 0)$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichseitiges Dreieck
  Berechne den Abstand von $A_{4}$ zum Koordinatenursprung $O (0 ∣ 0 ∣ 0)$
  Gegeben ist $A_{4}\left(\frac{\sqrt{75}}{3}\Big \vert-5\Big \vert 0\right)$ und das Dreieck ist gleichseitig.
  Der Abstand von $A_{4}$ zum Koordinatenursprung ist gleich $\dfrac{2}{3}\cdot h_D=\dfrac{2}{3}\cdot \sqrt{75}$ .
  $\left|\overrightarrow{\mathrm{OA}_{4}}\right|=\dfrac{2 \cdot \sqrt{75}}{3} \approx 5{,}77$
  Der Abstand von $A_{4}$ zum Koordinatenursprung beträgt rund $5{,}77\;\mathrm{LE}$ .
  Anmerkung: Der Abstand von $A_{4}$ zum Koordinatenursprung kann auch mit dem Satz des Pythagoras berechnet werden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben ist $A_{4}\left(\frac{\sqrt{75}}{3}|-5| 0\right)$ und das Dreieck ist gleichseitig.
  Der Abstand von $A_{4}$ zum Koordinatenursprung entspricht $\dfrac{2}{3}\cdot h_D$ .
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1 (Abbildung 1) und Aufgabe 3 (Abbildung 5).
1. Stellen Sie eine Koordinatengleichung der Ebene $F$ auf, in der die Fläche $A_{1} A_{2} B_{2} B_{1}$ liegt. (4 P)
  [Zur Kontrolle: $F: 3 \cdot x_{1}+4 \cdot x_{3}=150$ .]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene
  Stelle eine Koordinatengleichung der Ebene $F$ auf, in der die Fläche $A_{1} A_{2} B_{2} B_{1}$ liegt
  Eine Parametergleichung von $F$ ist $F: \vec{x}=\overrightarrow{O A_{1}}+v \cdot \overrightarrow{A_{1} A_{2}}+w \cdot \overrightarrow{A_{1} B_{2}}$
  $\def\arraystretch{1.25} \vec{x}=\left(\begin{array}{c}50 \\ -5 \\ 0\end{array}\right)+v \cdot\left(\begin{array}{c}0 \\ 10 \\ 0\end{array}\right)+w \cdot\left(\begin{array}{c}-40 \\ 10 \\ 30\end{array}\right), v, w \in \mathbb{R}$ .
  Die Orthogonalitätsbedingungen $\def\arraystretch{1.25} \left(\begin{array}{l}n_{1} \\ n_{2} \\ n_{3}\end{array}\right) \cdot\left(\begin{array}{l}0 \\ 10 \\ 0\end{array}\right)=0$ und $\def\arraystretch{1.25} \left(\begin{array}{l}n_{1} \\ n_{2} \\ n_{3}\end{array}\right) \cdot\left(\begin{array}{c}-40 \\ 10 \\ 30\end{array}\right)=0$ liefern das Gleichungssystem
  $\def\arraystretch{1.25} \begin{array}{rccccccc}\mathrm{I} & & & 10n_2 & & & = & 0 \\\mathrm{II} & -40n_1 & + & 10n_2 & + & 30n_3 & = & 0 \end{array}$
  Aus Gleichung $\mathrm{I}$ folgt $n_{2} = 0$ .
  Dann lautet Gleichung $\mathrm{II}$ : $-40n_1+30n_3=0\;\Rightarrow\;n_1=\dfrac{3}{4}n_3$ .
  Die Wahl von $n_{3}=4$ liefert als möglichen Normalenvektor von $\def\arraystretch{1.25} F: \overrightarrow{n_{F}}=\left(\begin{array}{l}3 \\ 0 \\ 4\end{array}\right)$ .
  Mit $\overrightarrow{O A_{1}}=\begin{pmatrix}50\\-5\\0\end{pmatrix}$ folgt dann $\overrightarrow{n_{F}}\circ\overrightarrow{O A_{1}}=\begin{pmatrix}3\\0\\4\end{pmatrix}\circ \begin{pmatrix}50\\-5\\0\end{pmatrix}=150$ und die Ebenengleichung ergibt sich zu $F: 3\cdot x_1+4\cdot x_3=150$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Eine Parametergleichung von $F$ ist $F: \vec{x}=\overrightarrow{O A_{1}}+v \cdot \overrightarrow{A_{1} A_{2}}+w \cdot \overrightarrow{A_{1} B_{2}}$ .
  Die Orthogonalitätsbedingungen $\vec n \circ \overrightarrow{A_{1} A_{2}}=0$ und $\vec n \circ \overrightarrow{A_{1} B_{2}}=0$ liefert ein Gleichungssystem, dessen Lösung ein möglicher Normalenvektor $\overrightarrow{n_{F}}$ von $F$ ist.
  Mit $\overrightarrow{n_{F}}$ und $\overrightarrow{O A_{1}}$ kann dann die Ebenengleichung von $F$ berechnet werden.
2. In der Mitte des Innenhofs steht ein Mast, dessen Spitze im Punkt $S (0 ∣ 0 ∣ 35)$ liegt.
  Zu einem bestimmten Zeitpunkt steht die Sonne so, dass die Sonnenstrahlen die Richtung $\def\arraystretch{1.25} \vec{r}=\left(\begin{array}{c}6 \\ 0 \\ -2\end{array}\right)$ besitzen.
  Untersuchen Sie, ob der Schatten der Spitze des Masts zu diesem Zeitpunkt innerhalb der Fläche $A_{1} A_{2} B_{2} B_{1}$ liegt. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
  Untersuche, ob der Schatten der Spitze des Masts zu diesem Zeitpunkt innerhalb der Fläche $A_{1} A_{2} B_{2} B_{1}$ liegt
  Gerade $h$ durch den Punkt $S$ mit dem Richtungsvektor $\vec{r}$ :
  $\def\arraystretch{1.25} h: \vec{x}=\left(\begin{array}{c}0 \\0 \\35\end{array}\right)+q \cdot\left(\begin{array}{c}6 \\0 \\-2\end{array}\right), q \in \mathbb{R}$ .
  Außerdem ist $F: 3\cdot x_1+4\cdot x_3=150$ .
  Berechnung des Schnittpunkts $Q$ von $F$ und $h$ :
  $3 \cdot 6 \cdot q+4 \cdot(35-2 \cdot q)=150$
  $\Rightarrow\;$ $18\cdot q+140-8\cdot q=150\;\Rightarrow\;10\cdot q=10\;\Rightarrow\;q=1$
  Setze $q = 1$ in $h$ ein:
  $\def\arraystretch{1.25} \overrightarrow{O Q}=\left(\begin{array}{c}0 \\ 0 \\ 35\end{array}\right)+1 \cdot\left(\begin{array}{c}6 \\ 0 \\ -2\end{array}\right)=\left(\begin{array}{c}6 \\ 0 \\ 33\end{array}\right) \Rightarrow Q(6|0| 33)$ .
  Die $x_{3}$ -Koordinate von $Q$ ist größer als $30$ . Der Schatten der Spitze des Masts liegt also nicht innerhalb der Fläche $A_{1} A_{2} B_{2} B_{1}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Erstelle die Gleichung der Geraden $h$ durch den Punkt $S$ mit dem Richtungsvektor $\vec{r}$ .
  Berechne den Schnittpunkt $Q$ von $F$ und $h$ $\;\Rightarrow\;\overrightarrow{O Q}$ .
  Vergleiche die $x_{3}$ -Koordinate von $Q$ mit der $x_{3}$ -Koordinate von $B_{1}$ (bzw. $B_{2}$ ).

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B3

Aufgabe 1

Gib die Koordinaten des Punktes B1B_{1}B1​ an

Hast du eine Frage oder Feedback?

Begründe, dass die Seitenfläche A2A3B3B2A_{2} A_{3} B_{3} B_{2}A2​A3​B3​B2​ ein Trapez ist

Berechne das Volumen des Körpers KKK

Hast du eine Frage oder Feedback?

Aufgabe 2

Zeige: Für jeden Wert von a mit 0≤a≤400 \leq a \leq 400≤a≤40 liegt der Punkt (50−a∣5∣0,75⋅a)(50-a|5| 0{,}75 \cdot a)(50−a∣5∣0,75⋅a) auf der Strecke A2B2‾\overline{A_{2} B_{2}}A2​B2​​

Hast du eine Frage oder Feedback?

Berechne die Länge der Stütze s1\mathrm{s}_{1}s1​

Hast du eine Frage oder Feedback?

Aufgabe 3

Ermittele rechnerisch die Koordinaten des Punktes PPP

Hast du eine Frage oder Feedback?

Berechne den Abstand von A4A_{4}A4​ zum Koordinatenursprung O(0∣0∣0)O(0|0| 0)O(0∣0∣0)

Hast du eine Frage oder Feedback?

Aufgabe 4

Stelle eine Koordinatengleichung der Ebene FFF auf, in der die Fläche A1A2B2B1A_{1} A_{2} B_{2} B_{1}A1​A2​B2​B1​ liegt

Hast du eine Frage oder Feedback?

Untersuche, ob der Schatten der Spitze des Masts zu diesem Zeitpunkt innerhalb der Fläche A1A2B2B1A_{1} A_{2} B_{2} B_{1}A1​A2​B2​B1​ liegt

Hast du eine Frage oder Feedback?

Gib die Koordinaten des Punktes $B_{1}$ an

Begründe, dass die Seitenfläche $A_{2} A_{3} B_{3} B_{2}$ ein Trapez ist

Berechne das Volumen des Körpers $K$

Zeige: Für jeden Wert von a mit $0 \leq a \leq 40$ liegt der Punkt $(50-a|5| 0{,}75 \cdot a)$ auf der Strecke $\overline{A_{2} B_{2}}$

Berechne die Länge der Stütze $\mathrm{s}_{1}$

Ermittele rechnerisch die Koordinaten des Punktes $P$

Berechne den Abstand von $A_{4}$ zum Koordinatenursprung $O (0 ∣ 0 ∣ 0)$

Stelle eine Koordinatengleichung der Ebene $F$ auf, in der die Fläche $A_{1} A_{2} B_{2} B_{1}$ liegt

Untersuche, ob der Schatten der Spitze des Masts zu diesem Zeitpunkt innerhalb der Fläche $A_{1} A_{2} B_{2} B_{1}$ liegt